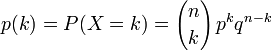Loi Binomiale

Loi binomiale

**Binomiale**
Densité de probabilité / Fonction de masse
Fonction de répartition
Paramètres	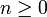$n \geq 0$ nombre d'épreuves (entier) 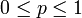$0\leq p \leq 1$ probabilité de succès (réel) $q = 1 - p$
Support	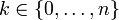$k \in \{0,\dots,n\}\!$
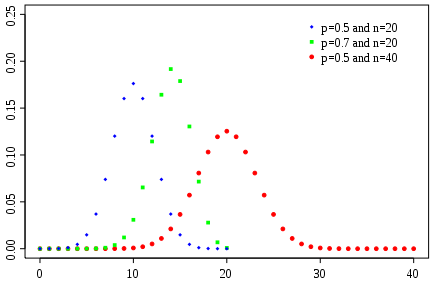
Densité de probabilité (fonction de masse)	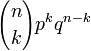${n\choose k} p^k q^{n-k} \!$
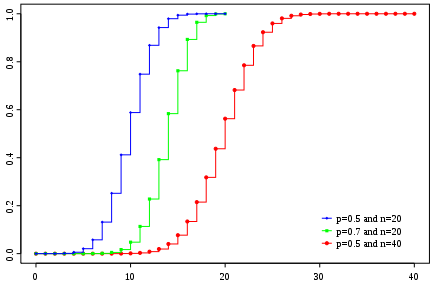
Fonction de répartition	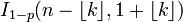$I_{1-p}(n-\lfloor k\rfloor, 1+\lfloor k\rfloor) \!$
Espérance	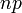$np\!$
Médiane (centre)	un des 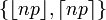$\{\lfloor np\rfloor, \lceil np \rceil\}$ ^[1]
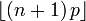
Mode	$\lfloor (n+1)\,p\rfloor\!$
Variance	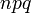$npq\!$
Asymétrie (statistique)	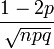$\frac{1-2p}{\sqrt{npq}}\!$
Kurtosis (non-normalisé)	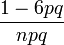$\frac{1-6pq}{npq}\!$
Entropie	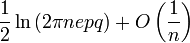$\frac{1}{2} \ln \left( 2 \pi n e p q \right) + O \left( \frac{1}{n} \right)$
Fonction génératrice des moments	$(q + pe^t)^n \!$
Fonction caractéristique	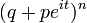$(q + pe^{it})^n \!$

En mathématiques, une loi binomiale de paramètres n et p est une loi de probabilité qui correspond à l'expérience suivante :

On renouvelle n fois de manière indépendante une épreuve de Bernoulli de paramètre p (expérience aléatoire à deux issues possibles, généralement dénommées respectivement « succès » et « échec », la probabilité d'un succès étant p, celle d'un échec étant $q = (1 - p)$ ). On compte alors le nombre de succès obtenus à l'issue des n épreuves et on appelle X la variable aléatoire correspondant à ce nombre de succès.

L'univers $X(\Omega )~$ désigne l'ensemble des entiers naturels de 0 à n.

La variable aléatoire suit une loi de probabilité définie par :

$p(k) = P(X = k)= {n \choose k} \, p^k q^{n-k}$

Cette formule fait intervenir le nombre des combinaisons de $k$ éléments parmi $n$ qui se note désormais 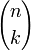${n\choose k}$ même si la notation 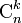$\mathrm{C}_{n}^{k}$ a été longtemps utilisée mais n'est plus reconnue. Notons que ce nombre de combinaisons se distingue du nombre des arrangements de $k$ éléments parmi $n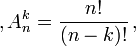$ $\,,A^k_n = \dfrac{n!}{(n-k)!}\,,$ du fait que dans une combinaison l'ordre des éléments n'importe pas. Et comme il y a $k!$ (prononcer factorielle k) façons d'ordonner $k$ éléments, le nombre des combinaisons se déduit du nombre des arrangements par la simple division 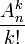$\dfrac{A^k_n}{k!}\,$ et on obtient :

${n\choose k} =\frac{n!}{k!(n-k)!}$

Cette loi de probabilité s'appelle la loi binomiale de paramètre (n ; p) et se note B(n ; p).

Calcul de p(k)

Une épreuve de Bernoulli conduit à la création d'un univers Ω = {S ; E}, (S pour Succès et E pour Echec).

n épreuves de Bernoulli indépendantes conduisent à la création d'un univers Ωⁿ constitué de n-uplets d'éléments de Ω, sur lequel peut se définir une probabilité produit. La probabilité de l'éventualité (S, S, ..., S, E, E, ..., E) avec k succès et n - k échecs a donc pour valeur p^kq^n-k.

Plus généralement, tout n-uplet formé de k succès et de n-k échecs aura pour probabilité p^kq^n-k quel que soit l'ordre d'apparition des S et des E.

L'évènement « X = k » est formé de tous les n-uplets comportant k succès et n - k échecs. La combinatoire permet de déterminer le nombre de n-uplets de ce type : il y en a autant que de parties à k éléments d'un ensemble à n éléments ; or chaque partie correspond à une façon de placer les k succès parmi les n places du n-uplet. Il y a donc 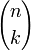${n \choose k}$ n-uplets, chacun ayant une probabilité égale à p^kq^n-k.

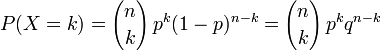Donc $P(X = k) = {n \choose k} \, p^k (1-p)^{n-k} = {n \choose k} \, p^k q^{n-k}$ .

Espérance, variance, écart type

X est la somme de n variables aléatoires indépendantes suivant toutes la (même) loi de Bernoulli de paramètre p, prenant la valeur 1 en cas de succès (probabilité p) et 0 en cas d'échec (probabilité (1-p)) ; ces variables aléatoires ont pour espérance p et pour variance p(1-p).

E(X) est donc la somme des espérances, soit np
V(X) est la somme des variances, soit np(1-p)
$\sigma_{X} = \sqrt{np(1-p)}$

Convergence

Pour de grandes valeurs de n, le calcul de 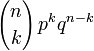${n \choose k} \, p^k q^{n-k}$ devient vite pratiquement impossible, sauf si l'on cherche à calculer le logarithme de cette expression au lieu de l'expression elle-même (et à condition d'utiliser l'approximation des factorielles par la formule de Stirling). On distingue deux cas :

Lorsque n tend vers l'infini et que p tend vers 0 avec np = a, la loi binomiale converge vers une loi de Poisson de paramètre a. En pratique, on remplace la loi binomiale par une loi de Poisson dès que n > 30 et np < 5 ou dès que n > 50 et p < 0.1.

Lorsque n tend vers l'infini et que p et q sont de même ordre de grandeur, la loi binomiale converge vers une loi normale d'espérance np et de variance npq. En pratique, on remplace une loi binomiale par une loi normale dès que n > 30, np > 5 et nq > 5

Démonstration de la convergence vers la loi normale

Supposons que $p (k)$ admette un extremum pour 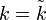$k = \tilde{k}$ . Alors, $ln p (k)$ admet un extremum 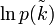$\ln p(\tilde{k})$ , car la fonction logarithme est monotone croissante. On calcule $ln p (k)$ à l'aide de la formule de Stirling :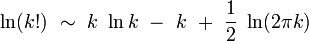

$\ln (k !) \ \sim \ k \ \ln k \ - \ k \ + \ \frac{1}{2} \ \ln ( 2 \pi k)$

Il vient :

$\ln p(k) \ \sim \ n \ \ln n \ - \ n \ + \ \frac{1}{2} \ \ln ( 2 \pi n) \ - \ \left[ \ k \ \ln k \ - \ k \ + \ \frac{1}{2} \ \ln ( 2 \pi k) \ \right]$

$\ - \ \left[ \ (n-k) \ \ln (n-k) \ - \ (n-k) \ + \ \frac{1}{2} \ \ln ( 2 \pi (n-k) \, ) \, \right] \ + \ k \ln p \ - \ (n-k) \ln (1-p)$

La dérivée par rapport à k donne :

$\frac{d~}{dk} \ln p(k) \ \sim \ \ln \left[ \, \frac{(n-k) \ p}{k \ (1 - p)} \, \right] \ + \ O \left( \frac{1}{k} \right)$

Pour annuler cette dérivée, il faut que l'argument du logarithme soit égal à un. On obtient alors la valeur de k qui rend le logarithme extremum :

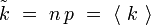
$\tilde{k} \ = \ n \, p \ = \ \langle \ k \ \rangle$

La valeur la plus probable est donc la valeur moyenne. La dérivée seconde vaut par ailleurs :

$\frac{d^2~}{dk^2} \ln p(k) \ \sim \ - \ \left[ \, \frac{1}{n-k} \ + \ \frac{1}{k} \, \right] \ + \ O \left( \frac{1}{k^2} \right)$

Calculée en 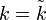$k = \tilde{k}$ , elle vaut :

$\frac{d^2~}{dk^2} \ln p(\tilde{k}) \ \sim \ - \ \left[ \, \frac{1}{np(1-p)} \, \right] \ = \ - \ \frac{1}{\sigma^2}$

On peut donc écrire le développement limité au second ordre suivant :

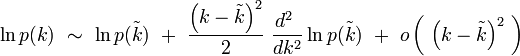
$\ln p(k) \ \sim \ \ln p(\tilde{k}) \ + \ \frac{\left( k - \tilde{k} \right)^2}{2} \ \frac{d^2~}{dk^2} \ln p(\tilde{k}) \ + \ o \left( \ \left( k - \tilde{k} \right)^2 \ \right)$

qui s'écrit compte-tenu de ce qui précède :

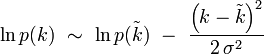
$\ln p(k) \ \sim \ \ln p(\tilde{k}) \ - \ \frac{\left( k - \tilde{k} \right)^2}{2 \, \sigma^2}$

soit en prenant l'exponentielle :

$p(k) \ \sim \ p(\tilde{k}) \ \exp \ \left[ - \ \frac{\left( k - \tilde{k} \right)^2}{2 \, \sigma^2} \ \right]$

On détermine la constante 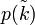$p(\tilde{k})$ avec la condition de normalisation des probabilités totales :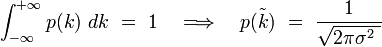

$\int_{- \infty}^{+ \infty} p(k) \ dk \ = \ 1 \quad \Longrightarrow \quad p(\tilde{k}) \ = \ \frac{1}{\sqrt{2 \pi \sigma^2 \ }}$

d'où la distribution gaussienne :

$p(k) \ = \ \frac{1}{\sqrt{2 \pi \sigma^2 \ }} \ \exp \ \left[ - \ \frac{\left( k - \langle \ k \ \rangle \, \right)^2}{2 \, \sigma^2} \ \right]$

Loi des grands nombres

La loi binomiale, son espérance et sa variance, ainsi que l'inégalité de Bienaymé-Tchebychev permettent de démontrer une version simple de la loi des grands nombres.

Références

↑ Hamza, K. (1995). The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions. Statist. Probab. Lett. 23 21–25.

Voir aussi

Lien externe

Articles de mathématiques en rapport avec les probabilités ou les statistiques

Statistiques descriptives • Analyse des données • Visualisation des données • Estimateurs • Tests statistiques • Séries temporelles et économétrie • Statistique Mathématique • Théorie des probabilités • Variables aléatoires • Inégalités • Théorèmes limites • Processus stochastiques • La mécanique statistique • Les statistiques et l'économie • Les statistiques et la sociologie • Les statistiques et les sciences • Les probabilités et les jeux • Les équations aux dérivées partielles et les probabilités

Portail des probabilités et des statistiques

Ce document provient de « Loi binomiale ».

Catégorie : Loi de probabilité

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi Binomiale de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Loi binomiale — Binomiale Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi binômiale — Loi binomiale Binomiale Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi binomiale — ● Loi binomiale loi théorique de distribution statistique telle que les fréquences soient égales aux coefficients binominaux … Encyclopédie Universelle
Loi binomiale négative — Binomiale négative Densité de probabilité / Fonction de masse La ligne rouge représente la moyenne et la ligne verte a pour longueur approximativement 2σ. Paramètres (réel) … Wikipédia en Français
Loi Normale — Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi Normale Reduite — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi de Gauss — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi de Laplace-Gauss — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi gaussienne — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi normale gaussienne — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Loi Binomiale

Loi binomiale

Sommaire

Calcul de p(k)

Espérance, variance, écart type

Convergence

Loi des grands nombres

Références

Voir aussi

Lien externe

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Loi Binomiale

Loi binomiale

Sommaire

Calcul de p(k)

Espérance, variance, écart type

Convergence

Loi des grands nombres

Références

Voir aussi

Lien externe

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link