Srinivasa Ramanujan

 Ne doit pas confondu avec cet autre mathématicien : C. P. Ramanujam (en).

Srinivasa Ramanujan
Naissance	22 décembre 1887 Erode (Inde britannique)
Décès	26 juin 1920 (à 32 ans) Kumbakonam (en), près de Chennai (Inde britannique)
Domicile	Tamil Nadu  Indes britanniques
Nationalité	Indienne
Champs	Mathématiques
Renommé pour	Constante de Landau-Ramanujan Nombre premier de Ramanujan Constante de Ramanujan-Soldner
modifier

Srinivâsa Aiyangâr Râmânujan, en tamoul : ஸ்ரீனிவாஸ ஐயங்கார் ராமானுஜன் (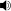), (22 décembre 1887 – 26 avril 1920) est un mathématicien indien. Ramanujan est né en Inde, dans une famille de brahmanes pauvre et orthodoxe. Il était un autodidacte et resta toujours très autonome. Il apprit les mathématiques à partir de deux uniques livres qu'il s'était procurés avant ses 15 ans : La Trigonométrie plane de S. Looney, et Synopsis of Elementary Results in Pure Mathematics de S. Carr qui contenait une liste de quelque 6 000 théorèmes sans démonstration. Ces deux ouvrages lui permirent d'établir une grande quantité de résultats sur la théorie des nombres, les fonctions elliptiques, les fractions continues et les séries infinies, tout en créant son propre système de représentation symbolique pour arriver à ces résultats. Jugeant son entourage académique dépassé, il publia plusieurs articles dans les journaux mathématiques indiens et tenta alors d'intéresser les mathématiciens européens à son travail par des lettres qu'il leur envoyait.

Une lettre de 1913 à Godfrey Harold Hardy contenait une longue liste de théorèmes sans démonstration. Hardy considéra tout d'abord cet envoi inhabituel comme une supercherie, puis - interpellé par l'étrangeté de certains théorèmes - en discuta longuement avec John Littlewood pour aboutir à la conviction que son auteur était certainement un « homme de génie »^[1]. Hardy lui répondit et invita Ramanujan à venir en Angleterre ; une collaboration fructueuse, en compagnie de Littlewood, en résulta.

Hardy déclara, à propos de certaines formules qu'il ne pouvait comprendre, qu'« un seul coup d'œil sur ces formules était suffisant pour se rendre compte qu'elles ne pouvaient être pensées que par un mathématicien de tout premier rang. Elles devaient être vraies, parce que personne n'eût pu avoir l'idée de les concevoir fausses »^[2]. Hardy aimait classer les mathématiciens sur une échelle de 1 à 100. Il s'attribuait 25, donnait 30 à Littlewood, 80 à David Hilbert et 100 à Ramanujan.

Tourmenté toute sa vie par des problèmes de santé, Ramanujan vit son état empirer en Angleterre ; il retourna en Inde en 1919 et mourut peu de temps après à Kumbakonam (en) (à 260 km de Madras) à l'âge de 32 ans. Il laissa derrière lui des livres entiers de résultats non démontrés (appelés Cahiers de Ramanujan) qui continuent d'être étudiés au début du XXI^e siècle.

Ramanujan travailla principalement en théorie analytique des nombres et devint célèbre pour ses formules sommatoires impliquant des constantes telles que π et e, des nombres premiers et la fonction partage d'un entier obtenue avec Godfrey Harold Hardy.

Ramanujan avait un raisonnement très rapide, ce qui faisait dire à certains de ses contemporains qu'il était un mathématicien « naturel », voire un génie^[3].

Biographie

Jeunesse

Ramanujan est né le 22 décembre 1887 à Erode, dans l'actuel État de Tamil Nadu en Inde, dans la résidence de ses grands-parents maternels. Son père, K. Srinivasa Iyengar, né à Tanjavûr, travaillait comme commis dans un magasin de sari. Sa mère, Komalatammal ou Komal Ammal était femme au foyer et chantait au temple. Ils vivaient dans une maison traditionnelle (aujourd'hui transformée en musée) de la rue Sarangapanidans à Kumbakonam (en). À l'âge d'un an et demi, sa mère accoucha d'un frère, Sadagopan, qui décédera environ trois mois plus tard. En décembre 1889, Ramanujan eut la variole mais guérit ; il déménagea ensuite dans la maison de ses grands parents maternels, à Kanchipuram, non loin de Madras. En novembre 1891, et de nouveau en 1894, sa mère donna naissance à deux enfants, cependant morts en bas âge.

Le 1^er octobre 1892, Ramanujan entra à l'école. Après la perte de son emploi de fonctionnaire à la cour de Kanchipuram, Ramanujan et sa mère retournèrent à Kumbakonam et on sait qu'il a été inscrit à l'école primaire. A la mort de son grand-père paternel, il fut renvoyé chez ses grands-parents maternels, qui ont alors déménagé à Madras. N'aimant pas l'école de Madras, il séchait les cours. C'est pourquoi sa famille fit appel à un agent de police pour s'assurer qu'il fréquentait l'école. Dans les six mois, Ramanujan était de retour à Kumbakonam.

Dès lors, le père de Ramanujan étant au travail toute la journée, sa mère pris grand soin de lui, et sa relation avec elle était étroite. Elle lui apprit notamment la tradition et le pourâna. Il apprit aussi à chanter des chants religieux, pour assister à pujas au temple. À l'école primaire Kangayan, Ramanujan était un brillant élève... En effet juste avant ses 10 ans, en novembre 1897, il termina premier de son quartier aux examens de primaire (en anglais, en tamoul , en géographie et en arithmétique). Avec ses partitions, il a terminé premier dans le quartier. Cette même année, Ramanujan rencontre pour la première fois les mathématiques formelles grâce à son passage dans l'enseignement secondaire.

A 11 ans, il avait déjà un niveau meilleur que deux élèves du collège. Plus tard il reçut un livre sur la trigonométrie avancée écrit par SL Loney. Dès 13 ans, il maîtrisait les connaissances issues de ce livre, et découvrit déjà quelques théorèmes. A 14 ans, il reçut ses certificats de mérite et une bourse universitaire. A l'âge de 16 ans, Ramanujan eut entre les mains un livre de George S. Carr, intitulé A Synopsis of Elementary Results in Pure and Applied Mathematics. C'est ce livre qui introduisit le plus profondément Ramanujan dans le monde des mathématiques. A 17 ans, il avait étudié en profondeur les nombres de Bernoulli et avait calculé la constante d'Euler jusqu'à 15 décimales. C'est ce qui explique que ses camarades affirmaient "rarement le comprendre".

Diplômé de la ville Higher Secondary School en 1904, Ramanujan reçut le prix K. Ranganatha Rao pour les mathématiques, des mains du directeur de l'école, M. Krishnaswami Iyer. C'est ce dernier qui introduisit Ramanujan au Government College à Kumbakonam en tant qu'étudiant exceptionnel. Mais à cause de son travail uniquement concentré sur les mathématiques il perdit sa bourse d'étude, et, en août 1905, il s'enfuit de la maison, en direction de Visakhapatnam. Plus tard, il s'inscrivit au collège Pachaiyappa, à Madras. Encore excellent en mathématiques, mais avec des résultats médiocres dans les autres disciplines telle la physiologie, Ramanujan rata l'examen, en décembre 1906 et de nouveau un an plus tard. Il continua cependant par la suite à poursuivre des recherches indépendantes en mathématiques, tout en vivant dans une pauvreté extrême, et n'ayant bien souvent rien à manger...

Vie en Inde

Le 14 juillet 1909, il se maria à Janaki Ammal. Mais, après le mariage, Ramanujan développa un testicule hydrocèle , un gonflement anormal de la tunique vaginale , et une membrane interne dans le testicule. En principe, ceci peut être traité à l'aide d'une opération chirurgicale peu compliquée libérant le fluide bloqué dans le scrotum. Sa famille ne put obtenir un médecin volontaire qu'en janvier 1910, pour effectuer l'opération gratuitement. Après une opération réussie, Ramanujan se mit à la recherche d'un emploi. Pour gagner de l'argent, il aida des étudiants à préparer leur examen de fin d'année, au Presidency College. Craignant pour sa santé, à la fin des années 1910, il demanda à son ami Radakrishna Iyer, de donner ses cahiers mathématiques au professeur Singaravelu Mudaliar, du Pachaiyappa's College, ou au professeur britannique Edward B. Ross, du Christian College^[4]. Après sa guérison, Ramanujan partit en train de Kumbakonam à Villupuram , ville sous contrôle français.

Attention des mathématiciens à Ramanujan

Il rencontra V. Ramaswamy Aiyer , fondateur de la société indienne de mathématique . Ramanujan, qui souhaitait un emploi au département des recettes où Aiyer travaillait, lui montra ses cahiers de mathématiques. Comme Aiyer le raconta plus tard:

« J'ai été frappé par la mathématique des résultats extraordinaires qu'il contient [les cahiers]. Je n'avais pas l'esprit d'étouffer son génie par un rendez-vous dans le bas de l'échelle du ministère du Revenu. »

Aiyer envoya Ramanujan, avec des lettres d'introduction, à des amis mathématicien à Madras, desquels il obtint des lettres d'introduction auprès de R. Ramachandra Rao, le secrétaire de la société indienne de mathématique.

Personnalité et vie religieuse

Ramanujan a été décrit comme une personne avec une disposition quelque peu timide et calme, un homme honoré avec des manières agréables^[5]. Il a vécu une existence plutôt spartiate à Cambridge. Les premiers biographes indiens de Ramanujan le décrivent comme un hindou rigoureusement orthodoxe. Ramanujan a crédité sa capacité de réflexion à sa Déesse familiale, Namagiri de Namakkal. Il a ainsi compté sur elle pour l'inspiration concernant son travail^[6] et revendiqua rêver des gouttes de sang qui symbolisent son époux masculin, Narasimha, avatar de Vishnou, après avoir reçu les visions de rouleaux de contenu mathématique complexe se révélant sous ses yeux^[7] Ramanujan disait souvent : « Une équation pour moi n'a aucune signification, à moins qu'elle ne représente une pensée de Dieu  »^[8],[9].

Hardy cite Ramanujan concernant les remarques de ce dernier qui pensait que toutes les religions lui semblaient également vraies^[10]. Hardy considéra que la piété de Ramanujan avait été idéalisée par les Occidentaux et exagérée - en référence à sa croyance, pas pratique - par des biographes indiens. En même temps, il a fait des remarques sur l'observance stricte de Ramanujan du végétarisme.

Formules

Ramanujan a donné la formule suivante :

Cette formule relie parfaitement une série infinie et une fraction continue pour donner une relation entre les deux plus célèbres constantes des mathématiques.

Jonathan (en) et Peter Borwein (en) ont démontré une deuxième formule qu'il avait découverte en 1910 :

Elle est très efficace puisqu'elle fournit 8 décimales à chaque itération.

Nombres de Ramanujan

• Un « nombre de Ramanujan » est un entier naturel qui peut s'exprimer comme la somme de deux cubes de deux façons différentes.
  Hardy rapporte l'anecdote suivante :

« Je me souviens que j'allais le voir une fois, alors qu'il était malade, à Putney. J'avais pris un taxi portant le numéro 1729 et je remarquai que ce nombre me semblait peu intéressant, ajoutant que j'espérais que ce ne fût pas mauvais signe.
- Non, me répondit-il, c'est un nombre très intéressant : c'est le plus petit nombre décomposable en somme de deux cubes de deux manières différentes. »

— G. H. Hardy, (en) Citations de Hardy

En effet, 9³ + 10³ = 1³ + 12³ = 1729.

• D'autres nombres ayant cette propriété avaient été trouvés par le mathématicien français Bernard Frénicle de Bessy (1602-1675) :
  • 2³ + 16³ = 9³ + 15³ = 4104
  • 10³ + 27³ = 19³ + 24³ = 20683
  • 2³ + 34³ = 15³ + 33³ = 39312
  • 9³ + 34³ = 16³ + 33³ = 40033

• Le plus petit nombre décomposable de deux manières différentes en somme de deux puissances quatrièmes est 635 318 657, et c'est Euler (1707-1783) qui l'a trouvé : 158⁴ + 59⁴ = 133⁴ + 134⁴ = 635318657.

• Un nième nombre taxicab, noté Ta(n) ou Taxicab(n), est le plus petit nombre qui peut être exprimé comme une somme de deux cubes positifs non nuls de n façons distinctes à l'ordre des opérandes près. Ainsi, Ta(1) = 2 = 1³ + 1³, Ta(2) = 1729 et Ta(3) = 87539319. Il existe une variante du nombre taxicab : un nombre cabtaxi est défini comme le plus petit nombre entier pouvant s'écrire de n façons différentes (à l'ordre des termes près) comme somme de deux cubes positifs, nuls ou négatifs.

• La preuve, de l'Américain David Auburn, est une pièce de théâtre évoquant ce concept. Elle a reçu un prix Pulitzer (2001). Les deux personnages principaux sont un mathématicien de génie qui a sombré dans la folie et sa fille qui doit prendre la relève. Une version française, en 2002, réunissait Rufus dans le rôle du mathématicien et Anouk Grinberg (puis Elsa Zylberstein) dans celui de la fille.

Annexes

Bibliographie

• Godfrey Harold Hardy, L'Apologie d'un mathématicien, Éditions Belin, 1985. ISBN 2-7011-0530-7
• Bernard Randé, Les carnets indiens de Srivanasa Ramanujan, Éditions Cassini, 2002. ISBN 2-84225-065-6
• G.H. Hardy, The Indian Mathematician Ramanujan, American Mathematical Monthly, Vol.44, n°3, mars 1937, pp 137-155.
• David Leavitt, Le comptable indien, Éditions Denoel, 2009, ISBN 2-207-26004-6

Notes et références

Voir aussi

Articles connexes

• Constante de Landau-Ramanujan
• Nombre premier de Ramanujan
• Nombre taxicab

Liens externes

• Panorama sur différents aspects de sa personne
• (en) Quelques notes sur sa vie et ses publications (format PostScript)
• (en) John J. O’Connor et Edmund F. Robertson, « Srinivasa Aiyangar Ramanujan », dans MacTutor History of Mathematics archive, université de St Andrews [lire en ligne] .
• (en) Journal dédié à sa vie, son travail et les domaines des mathématiques qu'il a influencés

• Portail du monde indien
• Portail des mathématiques