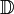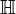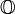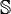Nombre Négatif

Nombre négatif

Un nombre négatif est un nombre qui est inférieur (inférieur ou égal) à zéro, tel que −3 ou −π. Ceux-ci comprennent les entiers négatifs, les nombres rationnels négatifs, les nombres irrationnels négatifs, les nombres réels négatifs. Zéro compte comme un nombre négatif. Lorsqu'un nombre est négatif et non nul, il est dit strictement négatif (cette terminologie diffère donc de la terminologie anglo-saxonne, pour laquelle un "positive number" est un nombre strictement positif, zéro n'étant considéré ni comme un nombre positif, ni comme un nombre négatif).

Les entiers négatifs peuvent être regardés comme une extension des entiers naturels, telle que l'équation x − y = z ait une solution significative pour toutes les valeurs de x et y ; l'ensemble des entiers positifs et négatifs s'appelle l'ensemble des entiers relatifs. Les autres ensembles de nombres peuvent être alors construits, comme des extensions progressivement plus élaborées ou comme des généralisations à partir des entiers.

Les nombres négatifs sont utiles pour décrire des valeurs sur une échelle qui descend au-dessous de zéro, telle que la température, et aussi en comptabilité où ils peuvent être utilisés pour représenter des dettes ou des déficits. En comptabilité, les dettes sont souvent représentées par des nombres écrits en rouge, ou par un nombre entre parenthèses.

Lorsque nous parlons de nombres positifs ou négatifs, les adjectifs positif et négatif doivent être pris au sens large, c'est-à-dire que zéro n'est pas exclu et zéro est donc un nombre (le seul) à la fois positif et négatif. Si nous considérons des nombres positifs ou négatifs mais non nuls, alors nous devons préciser strictement positifs ou strictement négatifs.

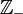L'ensemble des entiers relatifs négatifs est habituellement noté $\mathbb{Z}_-$ ,
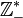l'ensemble des entiers relatifs strictement négatifs est habituellement noté $\mathbb{Z}_-^*$ ,
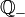l'ensemble des nombres rationnels négatifs est habituellement noté $\mathbb{Q}_-$ ,
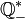l'ensemble des nombres rationnels strictement négatifs est habituellement noté $\mathbb{Q}_-^*$ ,
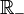l'ensemble des nombres réels négatifs est habituellement noté $\mathbb{R}_-$ ,
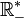l'ensemble des nombres réels strictement négatifs est habituellement noté $\mathbb{R}_-^*$ ,

Arithmétique impliquant les nombres négatifs

Addition et soustraction

Ajouter un nombre négatif revient à soustraire le nombre positif correspondant :

5 + (−3) = 5 − 3 = 2

−2 + (−5) = −2 − 5 = −7

Soustraire un nombre positif d'un plus petit nombre positif donne un résultat négatif :

4 − 6 = −2 (si vous avez en poche 4 € et que vous dépensez 6 €, alors vous avez une dette de 2 €).

Soustraire un nombre positif d'un nombre négatif donne un résultat négatif :

−3 − 6 = −9 (si vous avez une dette de 3 € et que vous dépensez encore 6 €, alors vous avez une dette de 9 €).

Soustraire un nombre négatif équivaut à ajouter le nombre positif correspondant:

5 − (−2) = 5 + 2 = 7 (si vous disposez d'une valeur nette de 5 € et que vous vous débarrassez d'une dette de 2 €, alors il vous reste une valeur 7 € en poche).

Aussi:

(−8) − (−3) = −5 (si vous avez une dette de 8 € et que vous vous débarrassez d'une dette de 3 €, alors vous aurez encore une dette de 5 €).

Multiplication

Le produit d'un nombre négatif par un nombre positif donne un résultat négatif: (−2) · 3 = −6. La raison de cela est que ce produit peut être interprété comme une addition répétée: (−2) · 3 = (−2) + (−2) + (−2) = −6. Nous pouvons l'interpréter autrement, si vous avez une dette de 2 €, et si votre dette est triplée, alors vous terminez avec une dette de 6 €.

La multiplication de deux nombres négatifs donne un résultat positif: (−3) · (−4) = 12. Cette situation ne peut pas être interprétée comme une addition répétée, et l'analogie avec une dette n'aide pas non plus. La raison essentielle de cette règle est que nous voulons que la multiplication soit distributive :

(3 + (−3)) · (−4) = 3 · (−4) + (−3) · (−4).

Le membre de gauche de cette relation est égal à 0 · (−4) = 0. Le côté droit est une somme de −12 + (−3) · (−4); pour que les deux membres soient égaux, nous avons besoin que (−3) · (−4) = 12.

Notion de nombre
Ensembles usuels	$\mathbb{N}$ Entier naturel • $\mathbb{Z}$ Entier relatif • $\mathbb{D}$ Nombre décimal • $\mathbb{Q}$ Nombre rationnel • $\mathbb{R}$ Nombre réel • $\mathbb{C}$ Nombre complexe
Extensions	$\mathbb{H}$ Quaternion • $\mathbb{O}$ Octonion • $\mathbb{S}$ Sédénion • Nombre complexe fendu • Tessarine • Nombre bicomplexe • Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • $\mathbb{Q}_p$ Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières	Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique	π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • $i$ Unité imaginaire • $e$ Constante de Neper • ℵ₀ Aleph-zéro • Table de constantes mathématiques
Notions connexes	Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif

Portail des mathématiques

Ce document provient de « Nombre n%C3%A9gatif ».

Catégorie : Propriété numérique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Négatif de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Nombre negatif — Nombre négatif Un nombre négatif est un nombre qui est inférieur (inférieur ou égal) à zéro, tel que −3 ou −π. Ceux ci comprennent les entiers négatifs, les nombres rationnels négatifs, les nombres irrationnels négatifs, les nombres réels… … Wikipédia en Français
Nombre négatif — Un nombre négatif est un nombre réel qui est inférieur (inférieur ou égal) à zéro, tel que −3 ou −π. Sommaire 1 Généralités 1.1 Interprétation 2 Arithmétique impliquant les nombres négatifs … Wikipédia en Français
négatif — négatif, ive [ negatif, iv ] adj. et n. • 1283; lat. negativus, de negare « nier » I ♦ (Opposé à affirmatif) 1 ♦ Qui exprime une négation, un refus. Réponse négative. « Le guide fit un signe de tête négatif » (Hugo). ♢ Qui exprime la négation.… … Encyclopédie Universelle
nombre — [ nɔ̃br ] n. m. • déb. XIIe; lat. numerus I ♦ 1 ♦ Concept de base des mathématiques, une des notions fondamentales de l entendement que l on peut rapporter à d autres idées (de pluralité, d ensemble, de correspondance), mais non définir.… … Encyclopédie Universelle
Nombre Imaginaire Pur — Cet article est un complément de nombre complexe. Un nombre imaginaire pur est un nombre complexe qui s écrit sous la forme ia avec a réel. Par exemple, i, i et 0 sont des imaginaires purs. Ce sont les nombres complexes dont la partie réelle est… … Wikipédia en Français
Nombre imaginaire — pur Cet article est un complément de nombre complexe. Un nombre imaginaire pur est un nombre complexe qui s écrit sous la forme ia avec a réel. Par exemple, i, i et 0 sont des imaginaires purs. Ce sont les nombres complexes dont la partie réelle… … Wikipédia en Français
Nombre Complexe — Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels. Les nombres… … Wikipédia en Français
Nombre Hyperréel — En mathématiques, les nombres hyperréels constituent une extension des nombres réels usuels, permettant de donner un sens rigoureux aux notions de quantité infiniment petite ou infiniment grande. Sommaire 1 Introduction : pourquoi les… … Wikipédia en Français
Nombre Positif — Un nombre positif est un nombre qui est supérieur (supérieur ou égal) à zéro, comme par exemple 3 ou e. Dans le cadre des nombres complexes positif exige implicitement réel, mais pour plus de clarté nous préférons dire « nombre réel… … Wikipédia en Français
Nombre hyperreel — Nombre hyperréel En mathématiques, les nombres hyperréels constituent une extension des nombres réels usuels, permettant de donner un sens rigoureux aux notions de quantité infiniment petite ou infiniment grande. Sommaire 1 Introduction :… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Nombre Négatif

Nombre négatif