Nombre Hyperréel

En mathématiques, les nombres hyperréels constituent une extension des nombres réels usuels, permettant de donner un sens rigoureux aux notions de quantité infiniment petite ou infiniment grande.

Sommaire 1 Introduction : pourquoi les hyperréels ? 2 Historique 3 Construction 4 Définitions 5 Un exemple d'utilisation 6 Notes et références 7 Voir aussi

Introduction : pourquoi les hyperréels ?

Les "infiniments petits" de l'Analyse du 17^ème siècle avaient suscité de violentes critiques, assez semblables à celles provoquées par l'introduction de "nombres imaginaires" de carré négatif. Les problèmes techniques correspondants ne purent cependant pas être résolus, ce qui amena la disparition progressive des infinitésimaux et leur remplacement, dû à Cauchy et Weierstrass, par les notions modernes de limite, de continuité, etc.

Cependant, on pouvait encore envisager d'adjoindre aux réels de nouveaux objets permettant de rendre rigoureux les raisonnements utilisant les infiniment petits, et diverses tentatives furent faites dans ce sens (par exemple par Hadamard et Du Bois-Raymond), mais cela sans grand succès, pour des raisons que seule la logique mathématique devait rendre claires.

Les travaux de Skolem montraient cependant dès 1930 qu'une extension des réels, autorisant un véritable calcul infinitésimal, était néanmoins possible. Il existe d'ailleurs en réalité plusieurs de ces extensions, mais le choix exact de l'une d'entre elles n'a pas de grandes conséquences pratiques (bien qu'elles ne soient pas toutes isomorphes) ; on appelle en général "nombres hyperréels" l'une quelconque d'entre elles.

Un nombre hyperréel (non réel) pourra représenter ainsi, par exemple une quantité « plus grande que tout entier » (donc "infiniment grande") ou « plus petite que l'inverse de tout entier » (donc infinitésimale).

Historique

Les nombres hyperréels furent introduits par Abraham Robinson dans les années 1960 dans le cadre de ses travaux sur l'analyse non standard. Robinson rejoignait les préoccupations d'Euler (et des autres analystes du 18^ème siècle) cherchant à donner un sens aux nombres infiniment grands et infiniment petits. La construction de Robinson utilisait essentiellement la théorie des modèles. Une construction plus explicite à l'aide d'ultraproduits fut découverte quelques années plus tard, et c'est celle qui va être exposée ici. Par la suite, une approche axiomatique plus générale de l'analyse non standard, la théorie des ensembles internes (Internal Set Theory, ou IST), fut proposée par Nelson, : elle se base sur l'axiomatique de Zermelo-Fraenkel à laquelle sont ajoutés trois axiomes nouveaux ; la description détaillée de ces axiomes et de leurs conséquences est donnée dans l'article : analyse non standard. Dans cette approche (qui a d'ailleurs des applications beaucoup plus générales que la construction d'infinitésimaux), on ne crée pas à proprement parler de nouveaux réels, mais on distingue parmi les réels une collection (qui n'est pas un ensemble) de réels standards, les autres se comportant par rapport à ceux-ci comme des infiniment petits ou des infiniment grands par exemple.

Construction

L'objectif est de contruire un surcorps 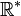de possédant des nombres infiniment grands et infiniment petits. Ce surcorps devra rester totalement ordonné et vérifier que tout nombre x non infiniment grand s'écrit x*+ε avec x* un nombre réel et ε un nombre infinitésimal.

Cette construction fait assez naturellement intervenir des suites de nombres réels ; ainsi la suite s'interprète comme un nombre infiniment petit et (n²) comme un infiniment grand. Les nombres réels sont préservés dans les suites constantes. L'addition et la multiplication des suites fournissent de bonnes bases pour obtenir une structure de corps. Malheureusement il manque l'ordre total : il n'est pas clair si le nombre hyperréel défini par la suite oscillante (1, -1, 1, -1, ...) est strictement positif ou strictement négatif. On observe ceci dit qu'étant donné 2 suites de réels, les ensembles d'indices ou l'une est supérieure à l'autre sont complémentaires. Choisir un ordre total sur les nombres hyperréels est donc équivalent à choisir une partie de N dans chaque couple de parties 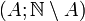. Ce dernier choix amène directement à la notion d'ultrafiltre sur N, de laquelle découle toute la construction qui suit^[1].

La construction des hyperréels se fait à partir d'un ultrafiltre U sur N qui contient toutes les parties cofinies de N. On ne peut malheureusement pas exhiber un tel ultrafiltre U, dont l'existence repose sur le raffinement du filtre des parties cofinies de N par le lemme de Zorn.

On construit l'ensemble M des suites de réels (z_n) dont l'ensemble des indices n où z_n = 0 est un élément de l'ultrafiltre. On peut écrire de manière condensée 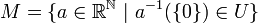. Un tel ensemble M est un idéal maximal de l'anneau commutatif des suites de réels 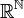. Donc l'anneau quotient 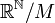est un corps ordonné commutatif qui contient .^[2] Cet ensemble (muni des lois induites par le quotient) est un surcorps de totalement ordonné. Il contient par exemple l'infiniment petit (1,1/2,1/3,...,1/n,...) (ou plus précisément la classe d'équivalence de cette suite). On perd par contre le théorème de la borne supérieure sur les nombres hyperréels.

On note que le cardinal de 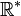est 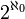et donc cet ensemble est équipotent à  ; cependant, on peut montrer que l'ensemble exact obtenu dépend de l'ultrafiltre choisi : tous les systèmes de nombres hyperréels construits ainsi ne sont pas isomorphes entre eux.

Définitions

Un nombre hyperréel x est dit

• infinitésimal, si |x| est strictement inférieur à tout réel positif

• infiniment grand si 1/x est infinitésimal.

• appréciable s'il n'est ni infiniment petit, ni infiniment grand.

Pour tout x appréciable, il existe un réel unique, la partie standard (ou l'ombre) de x (noté x*) tel que x-x* soit infinitésimal ; l'écriture en x*+ε de tout nombre hyperréel non infiniment grand provient d'une simple dichotomie (dans R) autorisée par l'ordre total sur 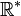. En effet un nombre hyperréel non infiniment grand est contenu dans un segment à bornes réelles ; on coupe successivement ce segment en 2 pour encadrer le nombre hyperréel de plus en plus précisément. Par le théorème des segments emboîtés, on obtient ainsi le nombre réel unique x*.

Un exemple d'utilisation

Avec les définitions précédentes, beaucoup de notions de l'analyse classique s'expriment de manière plus simple : ainsi, si est un infinitésimal non nul, la dérivée de f en a est l'ombre de l'hyperréel 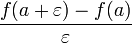 : tout se passe comme si on n'avait plus besoin de la notion de limite. On trouvera d'autres exemples (et des précisions sur la validité de ces raisonnements) dans l'article analyse non standard.

Notes et références

Voir aussi

• Analyse non-standard
• Ultrafiltre

Notion de nombre
Ensembles usuels	Entier naturel • Entier relatif • Nombre décimal • Nombre rationnel • Nombre réel • Nombre complexe
Extensions	Quaternion • Octonion • Sédénion • Nombre complexe fendu • Tessarine • Nombre bicomplexe • Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières	Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique	π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • i Unité imaginaire • e Constante de Neper • ℵ0 Aleph-zéro • Table de constantes mathématiques
Notions connexes	Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif

• Portail des mathématiques