Similitude (géométrie)

Pour les articles homonymes, voir Similitude.

Pour la similitude des triangles, voir Triangles semblables.

En géométrie euclidienne, une similitude est une transformation qui multiplie toutes les distances par une constante fixe, appelée son rapport. L'image de toute figure par une telle application est une figure semblable, c'est-à-dire intuitivement « de même forme ».

Dans ce dessin, les objets de même couleur sont semblables.

Sommaire

1 Rapports de longueurs, d'aires, ou de volumes
2 Exemples
3 Matrice de similitude
4 Similitudes planes
5 Etude générale

Rapports de longueurs, d'aires, ou de volumes

Le rapport d’une similitude est le coefficient k de proportionnalité entre les longueurs d’une première figure géométrique, et les longueurs correspondantes dans l’image de la première par la similitude. Autrement dit, la seconde figure reproduit la première à l’échelle k. Le nombre k × k ou k² est alors le coefficient de proportionnalité entre les aires correspondantes. Et k³ est le coefficient de proportionnalité entre les volumes correspondants, quand la similitude est définie dans l’espace à trois dimensions.

Par exemple, une similitude de rapport dix multiplie les longueurs par dix et les aires par cent. Si une similitude de rapport dix est définie dans l’espace à trois dimensions, elle multiplie les volumes par mille. Si une similitude de l’espace multiplie les volumes par deux, alors son rapport est le nombre positif k tel que k³ = 2. Ce nombre k est la racine cubique de 2, qui peut s’écrire 2^¹⁄₃.

Les similitudes de rapport 1 sont des isométries. Par exemple, les rotations, les translations et les symétries sont des similitudes de rapport 1.

Les homothéties sont des similitudes, et il faut noter l’ambiguïté du mot rapport. Le rapport d’une homothétie concerne des vecteurs, il peut être négatif, tandis que le rapport d’une similitude est un rapport de distances, toujours positif. Par exemple, une homothétie de rapport négatif -1 est une symétrie par rapport à son centre, ou une similitude de rapport positif 1, et d’angle 180° (un demi-tour). Dans tous les cas, une homothétie de rapport k est une similitude de rapport positif |k|.

Le propre des similitudes est d'envoyer toute figure sur une figure semblable, i.e. « de même forme » mais pas nécessairement « de même taille ». Par exemple, l'image d’un carré par une similitude est un carré. Et tout triangle rectangle isocèle est semblable à n’importe quel triangle rectangle isocèle. Si la similitude agit sur l’espace à trois dimensions, elle transforme un cube en un cube, et une sphère en une sphère. N’importe quelle figure géométrique est semblable à elle-même, car la fonction identité est une similitude particulière. Et n’importe quel cercle est semblable à n’importe quel cercle. Une similitude transforme un triangle équilatéral en un triangle équilatéral.

Exemples

Le carré CBFE reproduit le carré CTBA à l’échelle

\sqrt 2

, « parce que » son aire est double.

Exemple avec racine carrée de deux

Dans la figure de gauche, cherchons le rapport k de la similitude (directe, de centre C et d'angle 45°) qui transforme le carré CTBA en le carré CBFE, dont l'aire est double (car il est pavé par quatre triangles identiques aux deux triangles qui constituent le premier carré) :

$2AC^2=EC^2=(k~AC)^2=k^2AC^2.$

Ainsi, k²=2, donc le rapport k de la similitude est égal à la racine carrée de deux :

$\frac{FC}{BC}=\frac{EC}{AC}=k=\sqrt2$

(ce nombre est l'inverse de cos (45°) et c'est un irrationnel).

Plier en deux une feuille de papier

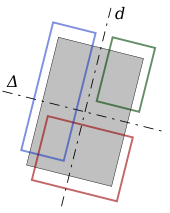
On peut plier en deux plusieurs fois de suite une feuille de papier rectangulaire. Le dessin de droite montre deux façons possibles de plier. L’opération superpose deux moitiés du rectangle, le pli est sur l’un ou l’autre axe de symétrie du rectangle. Les pointillés représentent les axes de symétrie d et Δ de la feuille grise initiale. Les rectangles obtenus par un pliage simple ou double sont dessinés avec des surfaces vides. Le rouge et le bleu résultent d’un seul pliage, soit dans un sens, soit dans l’autre (ils ont donc même aire, et sont semblables si et seulement s'ils sont isométriques c'est-à-dire si la feuille initiale est carrée) ; le vert résulte de deux pliages successifs.

Plier en deux divise par deux l’aire d’un rectangle. Par conséquent, pour que le rectangle rouge soit semblable au rectangle de la feuille grise initiale, il faut qu'il soit réduit à l'échelle $\scriptstyle\sqrt{1/2}=1/\sqrt2$ . Cette condition de similitude est remplie si, et seulement si, la feuille initiale a la forme du ratio d'aspect du papier standard international, c'est-à-dire si le rapport des deux côtés est de $\sqrt 2$ . Le rectangle vert sera alors, de même, semblable au rouge.

Le triangle HAC reproduit le triangle ABC à l’échelle

\sqrt 3 ⁄ 4

, « parce que » l’aire de HAC est égale aux trois quarts de l’aire de ABC.

Avec tan(60°) et sin(60°)

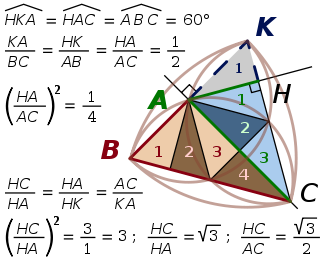
Le triangle BCK est équilatéral. Le point H est le projeté orthogonal sur (KC ) du milieu A de [BK ]. Huit triangles rectangles tous isométriques entre eux constituent un pavage de BCK, quatre de part et d’autre de la médiatrice de [BK ]. L’un des triangles du pavage est HKA. Une similitude de rapport un demi et d’angle négatif –120° transforme ABC en HKA, et divise son aire par 4 :

$\cos\,(\,60^\circ\,)\, =\, \tfrac{HA}{AC}\, =\, \tfrac{HK}{AB}\, =\, \tfrac{KA}{BC}\, =\, \tfrac{1}{2}\,;$

et $(\tfrac{HA}{AC})^2 =\, \tfrac{1}{4}.$

Une similitude de centre H et d’angle +90° transforme HKA en HAC en multipliant son aire par trois. Le rapport de cette similitude est :

$\tan\,(\,60^\circ\,)\, =\, \tfrac{HC}{HA}\, =\, \tfrac{HA}{HK}\, =\, \tfrac{AC}{KA}\, =\, \sqrt{3}.$

La composée des deux similitudes est la similitude de centre C, d’angle –30°, et de rapport sin (60°). Elle transforme deux côtés de ABC tracés en rouge en deux côtés de HAC tracés en vert. Les deux côtés correspondants de HKA sont en pointillé bleu. Ainsi les valeurs de tan (60°) et sin (60°) sont mises en évidence :

$\sin(\,60^\circ\,)\, =\, \tfrac{\tan(\,60^\circ\,)}{2}\, =\, \tfrac{\sqrt{3}}{2}.$

Le triangle STA reproduit ABC à l’échelle

\sqrt 5

, « parce que » son aire est cinq fois celle de ABC.

Avec racine carrée de cinq

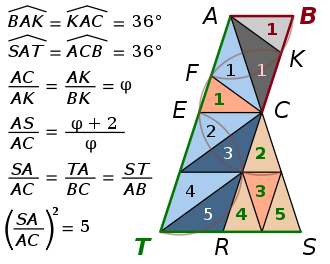
Le pentagone ABCST est pavé de douze triangles isocèles de deux sortes différentes. Deux d’entre eux pavent ABC, un de chaque sorte : BKA et AKC. Les dix autres triangles du pavage remplissent STA, cinq de chaque sorte. Cinq d’une sorte sont isométriques à AKC, ils ont deux angles égaux à 36°. Les cinq autres sont isométriques à BKA, ils ont deux angles égaux à 72°. Ainsi, l’aire de STA est cinq fois celle de ABC. Une similitude de rapport $\sqrt 5$ et d’angle 180° transforme ABC en STA. Elle transforme les deux côtés de ABC tracés en rouge en deux côtés de STA tracés en vert.

Les rapports de longueurs $\tfrac{AC}{AK}$ ou $\tfrac{AK}{BK}$ sont égaux à φ, le nombre d’or :

$2\,\cos(\,36^\circ\,)\, =\, \tfrac1{2\,\cos(\,72^\circ\,)}\, =\, \varphi.$

Le rapport de la précédente similitude peut donc s’écrire :

$\sqrt5\, =\, \tfrac{TA}{BC}\, =\, \tfrac{S\,T}{AB} =\, \tfrac{\varphi\,+\,2}{\varphi}.$

On en déduit cette valeur du nombre d’or :

$\varphi\, =\, \tfrac{1\,+\,\sqrt5}2.$

Matrice de similitude

Quand l’espace euclidien de dimension n est muni d’un repère orthonormé, une similitude correspond à une transformation de coordonnées, représentée par une matrice carrée inversible de taille n ou (n + 1), selon que l'origine des coordonnées est un point fixe ou pas. La matrice d’une similitude de rapport k a un déterminant égal en valeur absolue à k ⁿ : le coefficient de proportionnalité entre les aires d’une surface et de sa semblable si n = 2, ou entre les volumes des solides en relation par la similitude si n = 3. Si la similitude est directe, le déterminant de sa matrice est positif. Sinon il est négatif.

Afin de représenter toutes ces transformations par des multiplications matricielles de même format, le graphisme numérique utilise toujours les coordonnées homogènes. De longueur n + 1, la dernière ligne d’une telle matrice est alors toujours la même, inutile de la ranger en mémoire pour chaque transformation. Son dernier terme 1 est précédé de termes tous nuls.

Similitudes planes

Définition

Pour toute transformation f du plan euclidien, les propositions suivantes sont équivalentes.

f multiplie les distances par un réel strictement positif k ;
f conserve les rapports de distances ;
f conserve les angles géométriques (c'est-à-dire les mesures d'angles non orientés).

Une transformation du plan qui vérifie ces propositions est appelée une similitude du plan. Le nombre k est appelé le rapport de la similitude f. Une similitude qui conserve les angles orientés est appelée similitude directe

Les similitudes conservent donc les barycentres et les cercles. Réciproquement, toute transformation injective du plan qui conserve les cercles est une similitude.

Étude par les points fixes

Une similitude plane qui admet trois points fixes non alignés est l'identité du plan.
Une similitude plane qui admet deux points fixes distincts A et B est soit l'identité du plan, soit la symétrie axiale d'axe (AB).
Une similitude directe qui admet deux points fixes distincts est donc l'identité.

On peut donc classer les similitudes suivant le nombre de leurs points fixes :

l'identité, pour laquelle tous les points du plan sont fixes ;
les similitudes (indirectes) admettant une droite de points fixes : les symétries axiales (ou réflexions);
les similitudes directes avec un unique point fixe, qu'on appelle alors le centre de la similitude ;
les similitudes directes sans point fixe.

Similitudes planes directes

Mises à part les translations, toute similitude plane directe peut être décomposée en une homothétie et en une rotation de même centre.

Une isométrie qui conserve les angles orientés est appelée déplacement.

Toute similitude non directe (dite indirecte) est la composée d'une similitude directe et d'une réflexion.

Forme complexe

Les calculs sont adaptés au plan complexe. La traduction d'une similitude directe s'y exprime par $z' = a z + b$ , où a et b sont des complexes, a non nul. Le rapport de la similitude est alors $| a |$ , son angle $a r g (a)$ .

Cas spéciaux :

Dans le cas où $a = 1$ , la similitude est une translation.

Dans le cas où $a = - 1$ , la similitude est une symétrie centrale de centre $\Omega \left(\frac b2\right)$ . On peut aussi la considérer comme une rotation de centre $\Omega \left(\frac b2\right)$ et d'angle $π$ , ou encore une homothétie de centre $\Omega (\frac b2)$ et de rapport $k = - 1$ .

Dans le cas où $a \in \R^*\setminus\{ 1 \}$ , alors la similitude est une homothétie de centre $\Omega \left(\frac b{1-a}\right)$ et de rapport $a$ .

Théorème — Une transformation du plan est une similitude directe si et seulement son écriture complexe est de la forme $z' = a z + b$ , avec $a\in\C^*, b \in\C$ fixés.

Démonstration

Toute transformation qui s'écrit $z' = a z + b$ est une similitude directe.

En effet, si $a = 1$ c'est la translation dont le vecteur a pour affixe $b$ , et si $a\ne 1$ , le point $Ω$ d'affixe $\omega=\frac b{1-a}$ est fixe et la transformation s'écrit $z' - ω = k e i θ (z - ω)$ (avec $k = | a |$ et $θ = arg(a)$ ) donc c'est la composée de l'homothétie de centre $Ω$ et de rapport $k$ par la rotation de centre $Ω$ et d'angle $θ$ .

Toute similitude plane directe s'écrit $z' = a z + b$ .

Soient $O, A$ les points d'affixes respectives 0 et 1, $O', A'$ leurs images (distinctes) par cette transformation et $b, c$ leurs affixes. Soient $M\ne O$ un point quelconque, d'affixe $z$ , et $M'$ son image, d'affixe $z'$ . Alors

$\frac{O'M'}{O'A'}=\frac{OM}{OA}\qquad\text{et}\qquad\widehat{(\overrightarrow{O'A'},\overrightarrow{O'M'})}=\widehat{(\overrightarrow{OA},\overrightarrow{OM})},$ donc $\frac{z'-b}{c-b}=\frac{z-0}{1-0},$

c'est-à-dire, en notant $a$ le complexe $c - b$ (qui est non nul) :

$z'=az+b~$ (et cette équation est encore vérifiée pour

M = O, M' = O'

b = a .0 + b

Une similitude indirecte aura une écriture complexe de la forme $z' = a \bar{z} + b$ , où a et b sont complexes, a non nul.

Définition par deux points et leurs images

Soient $A, B, A^\prime, B^\prime$ quatre points du plan tels que : $A \neq B$ et $A' \neq B'$ . Il existe une unique similitude directe $S$ telle que $S(A)=A^\prime$ et $S(B)=B^\prime$

Démonstration

Soient $z A, z B, z A', z B'$ les affixes respectives de ces quatre points, et $S$ une similitude directe, qui s'écrit $z' = a z + b$ . Alors

$\begin{align}S(A)=A'\quad\text{et}\quad S(B)=B'&\Leftrightarrow z_{A'}=az_A+b\quad\text{et}\quad z_{B'}=az_B+b\\ &\Leftrightarrow z_{A'}=az_A+b\quad\text{et}\quad z_{B'}-z_{A'}=a(z_B-z_A)\\ &\Leftrightarrow a=\frac{z_{B'}-z_{A'}}{z_B-z_A}\quad\text{et}\quad b=z_{A'}-\frac{z_{B'}-z_{A'}}{z_B-z_A}z_A\\ &\Leftrightarrow a=\frac{z_{B'}-z_{A'}}{z_B-z_A}\quad\text{et}\quad b=\frac{z_{A'}z_B-z_{B'}z_A}{z_B-z_A},\end{align}$

d'où l'existence et l'unicité de la solution $(a,b)\in\C^*\times\C$ c'est-à-dire de la solution $S$ .

Le groupe des similitudes

La composée de deux similitudes f et g est une similitude, dont le rapport est le produit des rapports de f et g. Dans le cas de deux similitudes directes autres que des translations, on a : $S_{(\Omega,k,\theta)} \circ S_{(\Omega',k',\theta ')} = S_{(\Omega'',kk',\theta+\theta ')}$ lorsque $kk' \neq 1$ ou $\theta+\theta ' \neq 0$ . Dans le cas contraire, la composée est une translation.

La transformation réciproque d'une similitude f est une similitude, de rapport : l'inverse du rapport de f. Pour une similitude directe différente d'une translation, on a : $S^{-1}_{(\Omega,k,\theta)} = S_{(\Omega,\frac1 k,- \theta)}$ .

L'ensemble des similitudes du plan, muni de la loi de composition est donc un groupe, dont deux sous-groupes particuliers sont : le groupe des similitudes directes et le groupe des isométries. L'intersection des deux est le sous-groupe des déplacements.

Etude générale

Le cas des similitudes planes se généralise dans le cadre d'abord d'un espace euclidien, à savoir un espace vectoriel réel de dimension finie muni d'un produit scalaire <.|.>, puis d'un espace affine euclidien. Le produit scalaire donne un moyen de mesurer les distances. Ainsi, une application linéaire f sera une isométrie d'un tel espace si pour tous vecteurs x et y, <f(x)|f(y)>=<x|y> ; les isométries dans un espace euclidien forment un groupe appelé groupe orthogonal.

Une application linéaire f est une similitude (vectorielle) s'il existe un réel strictement positif k, appelé rapport de la similitude, tel que pour tous vecteurs x et y, <f(x)|f(y)>=k<x|y>. La transformation $f/\sqrt{k}$ est alors une isométrie : ainsi, toute similitude est la composée d'une isométrie et d'une homothétie : le groupe des similitudes est produit direct du groupe des isométries et du groupe des homothéties non nulles.

Dans un espace affine, le groupe affine est produit semi-direct du groupe linéaire par le groupe des translations. Dans un espace affine euclidien, les similitudes sont les éléments du sous-groupe produit semi-direct des similitudes vectorielles par les translations.

Portail de la géométrie

Catégorie :

Transformation géométrique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Similitude (géométrie) de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Similitude directe — Similitude (géométrie) Pour les articles homonymes, voir Similitude. Les objets de même couleur sont semblables. En géométrie, u … Wikipédia en Français
Similitude — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Similitude », sur le Wiktionnaire (dictionnaire universel) Le mot similitude possède plusieurs… … Wikipédia en Français
GÉOMÉTRIE — La géométrie est communément définie comme la science des figures de l’espace. Cette définition un peu incertaine risque de conduire à inclure dans la géométrie des questions qui ne sont géométriques que dans leur langage, mais relèvent en fait… … Encyclopédie Universelle
Geometrie synthetique — Géométrie synthétique La géométrie synthétique ou géométrie pure[1] est fondée sur une approche axiomatique (donc, « purement logique ») de la géométrie. Elle constitue une branche de la géométrie étudiant diverses propriétés et divers… … Wikipédia en Français
Géométrie Synthétique — La géométrie synthétique ou géométrie pure[1] est fondée sur une approche axiomatique (donc, « purement logique ») de la géométrie. Elle constitue une branche de la géométrie étudiant diverses propriétés et divers théorèmes uniquement… … Wikipédia en Français
Géométrie pure — Géométrie synthétique La géométrie synthétique ou géométrie pure[1] est fondée sur une approche axiomatique (donc, « purement logique ») de la géométrie. Elle constitue une branche de la géométrie étudiant diverses propriétés et divers… … Wikipédia en Français
similitude — (si mi li tu d ) s. f. 1° Ressemblance, rapport exact entre deux choses. Il n y a point de similitude entre ces deux objets. • Nous n avons d idée que de proche en proche ; nous ne concevons presque rien que par similitude, VOLT. Philos. 2e… … Dictionnaire de la Langue Française d'Émile Littré
Géométrie synthétique — La géométrie synthétique ou géométrie pure[1] est fondée sur une approche axiomatique (donc, « purement logique ») de la géométrie. Elle constitue une branche de la géométrie étudiant diverses propriétés et divers théorèmes uniquement… … Wikipédia en Français
GROUPES (mathématiques) - Groupes classiques et géométrie — Jusque vers 1800, la géométrie dite «élémentaire» est restée à peu de chose près ce qu’elle était dans l’Antiquité, tant dans sa substance que dans ses méthodes (l’invention de la «géométrie analytique» ayant à peu près exclusivement servi à… … Encyclopédie Universelle
Régulier (géométrie) — Polytope régulier Pour les articles homonymes, voir régulier. Le Dodécaèdre, un des cinq solides platoniciens. E … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Similitude (géométrie)

Sommaire

Rapports de longueurs, d'aires, ou de volumes