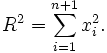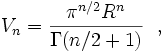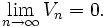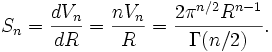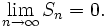Hypersphere

Hypersphere

Hypersphère

Hypersphère dans l'espace euclidien de dimension 3, c'est la sphère au sens usuel

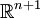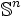En mathématiques, l'hypersphère est une généralisation de la sphère à un espace euclidien de dimension supérieure à 3. Elle constitue un des exemples les plus simples de variété et la sphère de dimension n, ou n-sphère, est plus précisément une hypersurface de l'espace euclidien \mathbb R^{n+1}, notée en général \mathbb S^n.

Sommaire

Définition

Soit E espace euclidien de dimension n+1. On appelle hypersphère de centre A et de rayon R nombre réel tel que R>0, l'ensemble des points M pour lesquels la distance AM vaut R.

Quitte à effectuer une translation, ce qui ne change rien aux propriétés géométriques, il est possible de se ramener à une hypersphère centrée en l'origine, dont l'équation s'écrit alors dans un système de coordonnées orthonormales

R^2=\sum_{i=1}^{n+1} x_i^2.\,

Par exemple

  • pour le cas n=0, l'hypersphère est constituée de deux points d'abscisses respectives R et -R.
  • pour le cas n=1, l'hypersphère est un cercle
  • pour le cas n=2, l'hypersphère est une sphère au sens usuel

Propriétés

Volume

Le volume de l'espace délimité par une hypersphère de dimension n-1 et de rayon R, qui est une boule euclidienne de dimension n, vaut :

V_n={\pi^{n/2}R^n\over\Gamma(n/2+1)}\ \ ,

où Γ désigne la fonction gamma. En particulier, on a :

n pair n impair
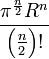
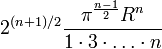
Vn \frac{\pi^{\frac{n}{2}}R^n}{\left(\frac{n}{2}\right)!} 2^{(n+1)/2}\frac{\pi^{\frac{n-1}{2}}R^n}{1\cdot 3 \cdot \dots \cdot n}

Le tableau suivant donne les valeurs du volume des 8 premières hypersphères de rayon 1 :

n Volume
Val. exacte Val. approchée
1 2 2
2 π 3,14159...
3 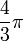\frac{4}{3}\pi 4,18879...
4 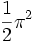\frac{1}{2}\pi^2 4,93480...
5 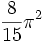\frac{8}{15}\pi^2 5,26379...
6 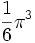\frac{1}{6}\pi^3 5,16771...
7 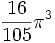\frac{16}{105}\pi^3 4,72478...
8 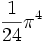\frac{1}{24}\pi^4 4,05871...

Le volume d'une telle hypersphère est maximal pour n=5. Pour n>5, le volume des hypersphères est décroissant quand n augmente. En particulier, la limite du volume à l'infini est nulle :

\lim_{n \to \infty}V_n = 0.

L'hypercube circonscrit à l'hypersphère unité possède des arêtes de longueur 2 et un volume 2n ; le rapport entre les volumes de l'hypersphère et de l'hypercube inscrit est décroissant en fonction de n.

Aire

L'aire de l'hypersphère de dimension n-1 et de rayon R peut être déterminée en prenant en compte la dérivée de son volume par rapport au rayon :

S_n=\frac{dV_n}{dR}=\frac{n V_n}{R}={2\pi^{n/2}R^{n-1}\over\Gamma(n/2)}.

Γ désigne ici aussi la fonction gamma.

Le tableau suivant donne les valeurs de l'aire des 8 premières hypersphères de rayon 1 (l'aire de l'hypersphère de dimension 1 est cependant omise) :

n Aire
Val. exacte Val. approchée
2 2π 6,28318...
3 4π 12,56637...
4 2π2 19,73920...
5 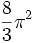\frac{8}{3}\pi^2 26,31894...
6 π3 31,00627...
7 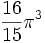\frac{16}{15}\pi^3 33,07336...
8 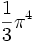\frac{1}{3}\pi^4 32,46969...

L'aire d'une telle hypersphère est maximale pour n=7. Pour n>7, l'aire des hypersphère est décroissant quand n augmente. En particulier, la limite de l'aire à l'infini est nulle :

\lim_{n \to \infty}S_n = 0.

Voir aussi

Articles connexes

Liens externes

  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Hypersph%C3%A8re ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Hypersphere de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Hypersphère — dans l espace euclidien de dimension 3, c est la sphère au sens usuel En mathématiques, l hypersphère est une généralisation de la sphère à un espace euclidien de dimension supérieure à 3. Elle constitue un des exemples les plus simples de… …   Wikipédia en Français

  • hypersphere — hy per*sphere (h[imac] p[ e]r*sf[=e]r), n. A mathematical object existing in more than three dimensions, analogous to the sphere in that all points on the surface are equidistant from the central point; a generalization of a sphere in more than… …   The Collaborative International Dictionary of English

  • hypersphere — hipersfera statusas T sritis fizika atitikmenys: angl. hypersphere vok. Hypersphäre, f rus. гиперсфера, f pranc. hypersphère, f …   Fizikos terminų žodynas

  • hypersphère — hipersfera statusas T sritis fizika atitikmenys: angl. hypersphere vok. Hypersphäre, f rus. гиперсфера, f pranc. hypersphère, f …   Fizikos terminų žodynas

  • Hypersphere (The History of the Galaxy) — Hypersphere is a spatial anomaly that exists alongside the normal space time continuum in the The History of the Galaxy series of novels by Russian science fiction writer Andrey Livadny. Similar to hyperspace in the TV series Babylon 5 ,… …   Wikipedia

  • hypersphere — hyperspherical /huy peuhr sfer i keuhl/, adj. /huy peuhr sfear , huy peuhr sfear /, n. Math. the generalization of a sphere to more than three dimensions. [1965 70; HYPER + SPHERE] * * * …   Universalium

  • hypersphere — noun a) The set of all points in a given hyperspace that are at a given distance from a given point. b) A zorb; the act of zorbing, entering a zorbing ball, strapping into a harness, and rolling down a hill …   Wiktionary

  • hypersphere — hy·per·sphere …   English syllables

  • hypersphere — ˈ ̷ ̷ ̷ ̷+ˌ noun Etymology: hyper + sphere : a sphere that is the analogue in hyperspace of the sphere in ordinary space …   Useful english dictionary

  • Calcul du volume de l'hypersphère — La dérivation suivante pour le calcul du volume de l hypersphère dépend des définitions précises de la sphère et de la boule. Le volume intérieur d une sphère est le volume de la boule délimitée par la sphère. Sommaire 1 Calcul 1.1 Formule de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”