- Nombre Bicomplexe
-
Nombre bicomplexe
En mathématiques, un nombre bicomplexe (voir l'article nombres multicomplexes) est un nombre écrit sous la forme
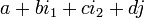 , où
, où 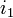 ,
, 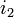 et
et 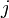 sont des unités imaginaires. Basé sur les règles de la multiplication des unités imaginaires, si
sont des unités imaginaires. Basé sur les règles de la multiplication des unités imaginaires, si 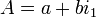 et
et 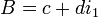 , alors le nombre bicomplexe peut être écrit
, alors le nombre bicomplexe peut être écrit 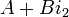 . Les nombres bicomplexes sont similaires aux nombres complexes, mais les deux parties sont complexes plutôt qu'une partie réelle. Les nombres bicomplexes se réduisent aux nombres complexes lorsque A et B sont des nombres réels.
. Les nombres bicomplexes sont similaires aux nombres complexes, mais les deux parties sont complexes plutôt qu'une partie réelle. Les nombres bicomplexes se réduisent aux nombres complexes lorsque A et B sont des nombres réels.L'ensemble de tous les nombres bicomplexes forment un anneau commutatif avec l'identité ; donc, la multiplication des nombres bicomplexes est à la fois commutative et associative et est distributive sur l'addition. Étant donné ceci et les règles pour la multiplication des unités imaginaires, deux nombres bicomplexes quelconques peuvent être multipliés. La multiplication des unités imaginaires est donnée par :
- i1 · i1 = −1
- i2 · i2 = −1
- j · j = 1
- i1 · i2 = j
- i1 · j = −i2
- i2 · j = −i1
La division n'est pas définie pour certains nombres complexes, puisque certains sont diviseurs de zéro; autrement dit, les bicomplexes ne forment pas un anneau intègre, et donc pas un anneau à division. Comme exemples de ceux-ci :
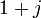 et
et 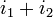 .
.Parmi les extensions des nombres complexes à des espaces vectoriels à quatre dimensions sur
 , les bicomplexes se distinguent des quaternions en « sacrifiant » l'existence des inverses et l'intégrité au profit de la commutativité de la multiplication.
, les bicomplexes se distinguent des quaternions en « sacrifiant » l'existence des inverses et l'intégrité au profit de la commutativité de la multiplication.Références
- G. Baley Price, An Introduction to Multicomplex Spaces and Functions, Marcel Dekker Inc., New York, 1991
- Dominic Rochon, A Bloch Constant for Hyperholomorphic Functions1 June, 2000
- Portail des mathématiques
Catégories : Nombre hypercomplexe | Algèbre linéaire
Wikimedia Foundation. 2010.
