Sedenion

Sedenion: Sédénion

En mathématiques, les sédénions, notés 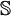$\mathbb S$ , forment une algèbre à 16 dimensions sur les réels. Leur nom provient du latin sedecim qui veut dire seize. Deux sortes sont actuellement connues :

Les sédénions obtenus par application de la construction de Cayley-Dickson

Les sédénions coniques (ou algèbre M).

Sommaire

1 Les sédénions de la construction de Cayley-Dickson

1.1 Arithmétique

2 Les sédénions coniques / algèbre M à 16-dim.

2.1 Arithmétique

3 Bibliographie

4 Articles connexes

Les sédénions de la construction de Cayley-Dickson

Arithmétique

À l'instar des octonions, la multiplication des sedénions n'est ni commutative ni associative. De plus, par rapport aux octonions, les sédénions perdent la propriété d'être alternatifs.

Les sédénions ont un élément neutre multiplicatif 1 et des inverses pour la multiplication, mais ils ne forment pas une algèbre de division. Cela parce qu'ils ont des diviseurs de zéro.

Chaque sedénion est une combinaison linéaire, à coefficients réels, des sédénions unités 1, e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀, e₁₁, e₁₂, e₁₃, e₁₄ et e₁₅, qui forment la base de l'espace vectoriel des sédénions. La table de multiplication de ces sédénions unitaires est établie comme suit :

× 1 e₁ e₂ e₃ e₄ e₅ e₆ e₇ e₈ e₉ e₁₀ e₁₁ e₁₂ e₁₃ e₁₄ e₁₅

1 1 e₁ e₂ e₃ e₄ e₅ e₆ e₇ e₈ e₉ e₁₀ e₁₁ e₁₂ e₁₃ e₁₄ e₁₅

e₁ e₁ -1 e₃ -e₂ e₅ -e₄ -e₇ e₆ e₉ -e₈ -e₁₁ e₁₀ -e₁₃ e₁₂ e₁₅ -e₁₄

e₂ e₂ -e₃ -1 e₁ e₆ e₇ -e₄ -e₅ e₁₀ e₁₁ -e₈ -e₉ -e₁₄ -e₁₅ e₁₂ e₁₃

e₃ e₃ e₂ -e₁ -1 e₇ -e₆ e₅ -e₄ e₁₁ -e₁₀ e₉ -e₈ -e₁₅ e₁₄ -e₁₃ e₁₂

e₄ e₄ -e₅ -e₆ -e₇ -1 e₁ e₂ e₃ e₁₂ e₁₃ e₁₄ e₁₅ -e₈ -e₉ -e₁₀ -e₁₁

e₅ e₅ e₄ -e₇ e₆ -e₁ -1 -e₃ e₂ e₁₃ -e₁₂ e₁₅ -e₁₄ e₉ -e₈ e₁₁ -e₁₀

e₆ e₆ e₇ e₄ -e₅ -e₂ e₃ -1 -e₁ e₁₄ -e₁₅ -e₁₂ e₁₃ e₁₀ -e₁₁ -e₈ e₉

e₇ e₇ -e₆ e₅ e₄ -e₃ -e₂ e₁ -1 e₁₅ e₁₄ -e₁₃ -e₁₂ e₁₁ e₁₀ -e₉ -e₈

e₈ e₈ -e₉ -e₁₀ -e₁₁ -e₁₂ -e₁₃ -e₁₄ -e₁₅ -1 e₁ e₂ e₃ e₄ e₅ e₆ e₇

e₉ e₉ e₈ -e₁₁ e₁₀ -e₁₃ e₁₂ e₁₅ -e₁₄ -e₁ -1 -e₃ e₂ -e₅ e₄ e₇ -e₆

e₁₀ e₁₀ e₁₁ e₈ -e₉ -e₁₄ -e₁₅ e₁₂ e₁₃ -e₂ e₃ -1 -e₁ -e₆ -e₇ e₄ e₅

e₁₁ e₁₁ -e₁₀ e₉ e₈ -e₁₅ e₁₄ -e₁₃ e₁₂ -e₃ -e₂ e₁ -1 -e₇ e₆ -e₅ e₄

e₁₂ e₁₂ e₁₃ e₁₄ e₁₅ e₈ -e₉ -e₁₀ -e₁₁ -e₄ e₅ e₆ e₇ -1 -e₁ -e₂ -e₃

e₁₃ e₁₃ -e₁₂ e₁₅ -e₁₄ e₉ e₈ e₁₁ -e₁₀ -e₅ -e₄ e₇ -e₆ e₁ -1 e₃ -e₂

e₁₄ e₁₄ -e₁₅ -e₁₂ e₁₃ e₁₀ -e₁₁ e₈ e₉ -e₆ -e₇ -e₄ e₅ e₂ -e₃ -1 e₁

e₁₅ e₁₅ e₁₄ -e₁₃ -e₁₂ e₁₁ e₁₀ -e₉ e₈ -e₇ e₆ -e₅ -e₄ e₃ e₂ -e₁ -1

Les sédénions coniques / algèbre M à 16-dim.

Arithmétique

À la différence des sédénions issus de la construction de Cayley-Dickson, qui sont construits sur l'unité (1) et 15 racines de l'unité négative (-1), les sédénions coniques sont construits sur 8 racines carrées de l'unité positive et négative. Ils partagent la non-commutativité et la non-associativité avec l'arithmétique des sédénions de Cayley-Dickson ("sédénions circulaires"), néanmoins les sédénions coniques sont modulaires, alternatifs, flexibles mais ne sont pas associatifs de puissances.

Les sédénions coniques contiennent à la fois les sous-algèbres des octonions circulaires, les octonion coniques et les octonions hyperboliques. Les octonions hyperboliques sont de manière calculatoire équivalents aux octonions fendus.

Les sédénions coniques contiennent des éléments idempotents, nilpotents et des diviseurs de zéro. Avec l'exception de leurs éléments nilpotents et zéro, l'arithmétique est close avec le respect des opérations de puissance et de logarithme.

Bibliographie

Carmody, Kevin: Circular and Hyperbolic Quaternions, Octonions and Sedenions, Applied Mathematics and Computation 28:47-72 (1988)

Carmody, Kevin: Circular and Hyperbolic Quaternions, Octonions and Sedenions - Further results, Applied Mathematics and Computation, 84:27-47 (1997)

Imaeda, K., Imaeda, M.: Sedenions: algebra and analysis, Applied Mathematics and Computation, 115:77-88 (2000)

Carmody, Kevin: Circular and Hyperbolic Quaternions, Octonions and Sedenions - Part III, Online at http://www.kevincarmody.com/math/sedenions3.pdf (2006)

Articles connexes

nombre hypercomplexe

quaternions

biquaternions

octonions

Notion de nombre

Ensembles usuels $\mathbb{N}$ Entier naturel • $\mathbb{Z}$ Entier relatif • $\mathbb{D}$ Nombre décimal • $\mathbb{Q}$ Nombre rationnel • $\mathbb{R}$ Nombre réel • $\mathbb{C}$ Nombre complexe

Extensions $\mathbb{H}$ Quaternion • $\mathbb{O}$ Octonion • $\mathbb{S}$ Sédénion • Nombre complexe fendu • Tessarine • Nombre bicomplexe • Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • $\mathbb{Q}_p$ Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel

Propriétés particulières Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand

Exemples d’importance historique π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • $i$ Unité imaginaire • $e$ Constante de Neper • ℵ₀ Aleph-zéro • Table de constantes mathématiques

Notions connexes Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif

Portail des mathématiques

Ce document provient de « S%C3%A9d%C3%A9nion ».

Catégories : Nombre hypercomplexe | Algèbre

Contenu soumis à la licence CC-BY-SA. Source : Article Sedenion de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Sedenion — In abstract algebra, sedenions form a 16 dimensional algebra over the reals. The set of sedenions is denoted as mathbb{S}. Two types are currently known: # Sedenions obtained by applying the Cayley Dickson construction # Conic sedenions ( 16… … Wikipedia
Sédénion — En mathématiques, les sédénions, notés , forment une algèbre à 16 dimensions sur les réels. Leur nom provient du latin sedecim qui veut dire seize. Deux sortes sont actuellement connues : Les sédénions obtenus par application de la… … Wikipédia en Français
Sedenion — … Deutsch Wikipedia
Hypercomplex number — The term hypercomplex number has been used in mathematics for the elements of algebras that extend or go beyond complex number arithmetic.Hypercomplex numbers have had a long lineage of devotees including Hermann Hankel, Georg Frobenius, Eduard… … Wikipedia
Hypercomplexe — Nombre hypercomplexe En mathématiques, le terme nombre hypercomplexe est utilisé pour désigner les éléments des algèbres qui sont étendues ou qui vont plus loin que l arithmétique des nombres complexes. Les nombres hypercomplexes ont eu un grand… … Wikipédia en Français
Hypercomplexes — Nombre hypercomplexe En mathématiques, le terme nombre hypercomplexe est utilisé pour désigner les éléments des algèbres qui sont étendues ou qui vont plus loin que l arithmétique des nombres complexes. Les nombres hypercomplexes ont eu un grand… … Wikipédia en Français
Nombre Hypercomplexe — En mathématiques, le terme nombre hypercomplexe est utilisé pour désigner les éléments des algèbres qui sont étendues ou qui vont plus loin que l arithmétique des nombres complexes. Les nombres hypercomplexes ont eu un grand nombre de partisans… … Wikipédia en Français
Nombre hypercomplexe — En mathématiques, le terme nombre hypercomplexe est utilisé pour désigner les éléments des algèbres qui sont étendues ou qui vont plus loin que l arithmétique des nombres complexes. Les nombres hypercomplexes ont eu un grand nombre de partisans… … Wikipédia en Français
Nombres hypercomplexes — Nombre hypercomplexe En mathématiques, le terme nombre hypercomplexe est utilisé pour désigner les éléments des algèbres qui sont étendues ou qui vont plus loin que l arithmétique des nombres complexes. Les nombres hypercomplexes ont eu un grand… … Wikipédia en Français
Alternative algebra — In abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have *x(xy) = (xx)y *(yx)x = y(xx)for all x and y in the algebra. Every associative algebra is… … Wikipedia

Dictionnaires et Encyclopédies sur 'Academic'

Sedenion

Sédénion

Sommaire

Les sédénions de la construction de Cayley-Dickson

Arithmétique

Les sédénions coniques / algèbre M à 16-dim.

Arithmétique

Bibliographie

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Notion de nombre
Ensembles usuels	$\mathbb{N}$ Entier naturel • $\mathbb{Z}$ Entier relatif • $\mathbb{D}$ Nombre décimal • $\mathbb{Q}$ Nombre rationnel • $\mathbb{R}$ Nombre réel • $\mathbb{C}$ Nombre complexe
Extensions	$\mathbb{H}$ Quaternion • $\mathbb{O}$ Octonion • $\mathbb{S}$ Sédénion • Nombre complexe fendu • Tessarine • Nombre bicomplexe • Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • $\mathbb{Q}_p$ Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières	Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique	π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • $i$ Unité imaginaire • $e$ Constante de Neper • ℵ₀ Aleph-zéro • Table de constantes mathématiques
Notions connexes	Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Sedenion

Sédénion

Sommaire

Les sédénions de la construction de Cayley-Dickson

Arithmétique

Les sédénions coniques / algèbre M à 16-dim.

Arithmétique

Bibliographie

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link