- Hexagone
-
Pour les articles homonymes, voir Hexagone (homonymie).Hexagone régulier 
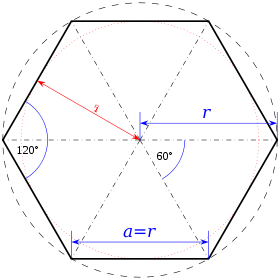
Représentation d'un hexagone régulierType Polygone régulier Symbole de Schläfli {6} Diagramme de Coxeter-Dynkin 
Groupe de symétrie Diédral (D6) Angle interne 120° Propriétés Convexe, cyclique, équilatéral, isogonal, isotoxal modifier 
Un hexagone (du grec hexi = six et gonia = angle) est un polygone à six sommets et six côtés. Les angles internes d'un hexagone régulier sont tous de 120° et ses côtés sont de même mesure. Les hexagones réguliers peuvent se juxtaposer les uns les autres sans laisser aucune lacune, comme les carrés et les triangles équilatéraux, et sont ainsi utiles pour construire des pavages. Les cellules des rayons dans une ruche d'abeilles à miel sont hexagonales pour cette raison et parce que cette forme permet une utilisation efficace de l'espace et des matériaux de construction.
Sommaire
Calcul de la surface
La surface d'un hexagone régulier de côté
estLa surface d'un hexagone régulier dont le rayon du cercle inscrit est
, alors l'aire 
estCalcul de la surface par décomposition en triangles
La surface d'un hexagone régulier isométrique peut aussi se calculer avec la formule suivante :
Déduit de la formule générale du calcul de l'aire d'un polygone régulier possédant
côtés (
) :Cette formule permet de calculer l'aire en divisant l'hexagone en 6 triangles équilatéraux. Comme r = a, l'apothème
se déduit à l'aide de la formule de Pythagore 
.On a donc pour un hexagone régulier
.On en déduit(pour un hexagone régulier)
.- : Longueur d'un des 6 côtés de l'hexagone.
- : Longueur de l'apothème (apothème : ligne droite perpendiculaire à l'un des côtés qui rejoint le centre de l'hexagone)
: Longueur du rayon (rayon : ligne droite du centre de l'hexagone à l'un des 6 sommets)- : Nombre de côté du polygone régulier (pour la formule générale).
Propriétés générales
Hexagone croisé Hexagone convexe Hexagone concave Sommets Côtés Diagonales 6 6 9 Hexagone régulier
Un hexagone régulier est un hexagone convexe inscrit dans un cercle et dont tous les côtés ont la même longueur (et les angles la même mesure). On peut considérer qu'il est constitué d'un certain assemblage de six triangles équilatéraux, égaux entre eux.
Symétrie
Un hexagone possède 6 axes de symétrie:
3 axes de symétrie passant par les sommets opposés et le centre, 3 axes de symétrie passant par les points milieux des côtés opposés et le centre.
Hexagone et triangle équilatéral
Un hexagone régulier possède 6 triangles équilatéraux.
Construction d'un hexagone régulier
Un hexagone régulier est constructible car il vérifie le théorème de Gauss-Wantzel [1]: 6 est le produit de 2 (en effet, 2 est puissance de 2) et de 3 (3 est un nombre de Fermat).
Il est possible de construire un hexagone régulier avec un compas et une règle, en suivant la méthode des éléments d'Euclide, qui consiste à construire 6 triangles équilatéraux:
On construit un cercle C de centre O et de diamètre [AD] (1 - 2) . Puis, on trace un arc de cercle de centre A et de rayon [AO]: l'arc de cercle coupe le cercle C en B et en F (3). Les diamètres de C passant par B et par F coupent le cercle en C et en E (4 - 5). En joignant les points du cercle A, B, C, D, E et F (6 - 11), on obtient un hexagone régulier.
...
Pavages
L'hexagone permet de créer un pavage périodique.
Dans la nature
Les alvéoles d'abeille, construits afin de stocker le miel et le pollen ou les œufs et les larves, sont des prismes juxtaposés d’axes horizontaux qui constituent le gâteau de cire. Ce gâteau de cire est ainsi formé de deux séries d’alvéoles hexagonaux se rejoignant en leur base. L'hexagone est une figure optimale, pour l'abeille. Non seulement elle permet de paver le plan, mais, de plus, elle correspond à un optimum isopérimétrique, c'est-à-dire que parmi les figures régulières qui permettent de paver l'espace, l'hexagone correspond à la plus grande surface possible pour un périmètre donné. Aucune autre figure permettant de paver l'espace n'utilise moins de cire que celle adoptée par les abeilles. Cette remarque est initialement l'œuvre de Pappus, un géomètre grec de l'antiquité.
La jonquille possède 6 pétales soudés en tube hexagonal autour de l'ovaire. En effet, c'est ici aussi la plus grande surface possible pour attirer les insectes en son sein.
Au niveau de la région boréale du pôle Nord de Saturne la sonde spatiale Cassini (2006) et Voyager (1980) ont observés à 78 degrés de latitude nord, via un spectromètre infrarouge, une structure hexagonale. Elle est située à 902 000 km au-dessus des nuages et est particulièrement persistante.
Dans la dynamique des fluides, les flux en rotation produisent des structures instables, telles que des vortex. Ils sont à l'origine des tornades, mais aussi des courants et autres écoulements. La figure géométrique ainsi observable est appelée « seau de Newton » ou tout simplement un hexagone.
Des bulles de savon s'organisent toutes en hexagones lorsqu'il y en a de trop dans un espace fermé. Elles prennent alors la forme d'hexagone, qui correspond ici à un optimum isopérimétrique.
Les fentes de dessiccation et les coulées de lave refroidies prennent cette même configuration géométrique.
Un autre élément dans la nature à forme hexagonale connu est le flocon de neige. Les molécules d'eau qui les composent imposent des angles réguliers à ses cristaux.
Il existe aussi de nombreuses molécules et atomes qui prennent cette forme grâce à leurs liaisons covalentes.
Usages
-
Ballon de football aux couleurs du Brésil. Normalisée, la forme d'un ballon de football est composée de 20 faces hexagonales et 12 pentagonales.
-
Vue intérieure verticale de la structure hexagonale, laissant transparaître l’étoile de David, du Mémorial de la synagogue, brûlée en 1938 durant la Nuit de cristal, sur la Platz der Synagoge (place de la Synagogue) à Göttingen (Allemagne).
Hexagramme
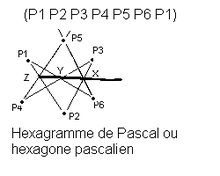
Article détaillé : hexagramme.L’hexagramme de Pascal
Hexagramme de Pascal
Un hexagramme de Pascal est un hexagone irrégulier très particulier. Il est tel que les côtés opposés se coupent en trois points alignés. Cette configuration, inventée par Blaise Pascal, est très utile pour l'étude des ellipses, hyperboles, paraboles, cercles.
Autres
De par sa forme grossièrement hexagonale, la France métropolitaine est souvent appelée "Hexagone".
Liens internes
Notes et références
- Un polygone régulier à n côtés est constructible si et seulement si n est le produit d'une puissance de 2 et de k nombres de Fermat premiers tous différents.
Wikimedia Foundation. 2010.
