Nombre Réel Calculable

Nombre Réel Calculable

Nombre réel calculable

En informatique et algorithmique, un nombre réel calculable est un réel pour lequel il existe un algorithme ou une machine de Turing permettant d'énumérer tous les chiffres de son développement décimal. Cette notion a été mise en place et développée par Turing.

L'ensemble des réels calculables est un corps (les lois d'un corps étant calculables) dénombrable (un algorithme étant une suite finie de lettres d'un alphabet fini, l'ensemble des algorithmes, et donc a fortiori des nombres calculables, est dénombrable). Cet ensemble contient, par exemple, tous les nombres algébriques, ou des constantes célèbres comme π ou γ. La plupart des réels sont donc non calculables (complémentaire d'un ensemble dénombrable), bien qu'il soit généralement difficile de les définir (puisqu'on ne peut les calculer...). Quelques exemples remarquables existent cependant, comme la constante Oméga de Chaitin ou les nombres définis par le castor affairé.

Sommaire

Construction de nombres calculables

Tout nombre réel est la limite d'une suite de nombres rationnels ; ainsi s'il est possible d'expliciter un terme général pour une telle suite, le nombre qui en est la limite est calculable.

On sait par exemple que:

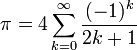
\pi =4 \sum_{k = 0}^{\infty}\frac{(-1)^{k}}{2k+1}

Il est donc possible de déterminer des rationnels approchant π avec une précision arbitraire (la théorie sur les séries alternées permet même de savoir pour quel entier m il faut calculer 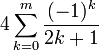4 \sum_{k = 0}^{m}\frac{(-1)^{k}}{2k+1} pour avoir un nombre donné de décimales exactes).

Mieux, tout nombre donné par une suite explicite à partir de nombres dont on a déjà montré qu'ils sont calculables l'est également. Par exemple non seulement e est calculable car 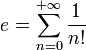e = \sum_{n = 0}^{+\infty} {1 \over n!} mais eπ l'est également car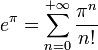 e^\pi = \sum_{n = 0}^{+\infty} {\pi^n \over n!}

Donc pour toute fonction calculable, l'image d'un nombre calculable est un nombre calculable ; par exemple le cosinus d'un rationnel donné est calculable.

En revanche, si on sait que 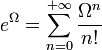e^\Omega = \sum_{n = 0}^{+\infty} {\Omega^n \over n!}, eΩ n'en est pas calculable pour autant puisque Ω ne l'est pas (d'ailleurs eΩ n'est pas calculable sinon Ω = log(eΩ) le serait).

On pourrait être tenté de dire que, s'il y a un ensemble des nombres calculables, et s'il est dénombrable, l'application du procédé diagonal de Cantor à cet ensemble fournirait bien un algorithme pour calculer un nouveau nombre, ce qui conduirait à une contradiction.

La réponse de Turing est que l'on ignore comment attribuer un numéro à chaque nombre calculable, or ceci doit être fait préalablement à la diagonalisation - voir le chapitre 8 de l'ouvrage de 1936 cité ci-dessous.

Nombre complexe calculable

Par extension, on appelle nombre complexe calculable un nombre complexe dont les parties réelle et imaginaire sont simultanément calculables.

Bibliographie

  • Alan Turing et Jean-Yves Girard, La machine de Turing, Editions du Seuil Paris, 1995
  • On computable numbers, with an application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, series 2, 1936, vol 42, pp.230-265 (version en ligne)
  • Klaus Weihrauch, Computable analysis: an introduction, Springer, Texts in theoretical computer science, ISBN 3-540-66817-9 (version en ligne)

Articles connexes

Liens externes

http://www.thocp.net/biographies/papers/turing_oncomputablenumbers_1936.pdf

Notion de nombre
Ensembles usuels \mathbb{N} Entier naturel • \mathbb{Z} Entier relatif • \mathbb{D} Nombre décimal • \mathbb{Q} Nombre rationnel • \mathbb{R} Nombre réel • \mathbb{C} Nombre complexe Mathématiques
Extensions \mathbb{H} Quaternion • \mathbb{O} Octonion • \mathbb{S} Sédénion • Nombre complexe fendu • Tessarine • Nombre bicomplexe • Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • \mathbb{Q}_p Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • i Unité imaginaire • e Constante de Neper • ℵ0 Aleph-zéro • Table de constantes mathématiques
Notions connexes Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre r%C3%A9el calculable ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Réel Calculable de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Nombre reel calculable — Nombre réel calculable En informatique et algorithmique, un nombre réel calculable est un réel pour lequel il existe un algorithme ou une machine de Turing permettant d énumérer tous les chiffres de son développement décimal. Cette notion a été… …   Wikipédia en Français

  • Nombre réel calculable — En informatique et algorithmique, un nombre réel calculable est un réel pour lequel il existe un algorithme ou une machine de Turing permettant d énumérer tous les chiffres de son développement décimal. Cette notion a été mise en place et… …   Wikipédia en Français

  • Réel calculable — Nombre réel calculable En informatique et algorithmique, un nombre réel calculable est un réel pour lequel il existe un algorithme ou une machine de Turing permettant d énumérer tous les chiffres de son développement décimal. Cette notion a été… …   Wikipédia en Français

  • Nombre Réel — Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs ou nuls,… …   Wikipédia en Français

  • Nombre reel — Nombre réel Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs… …   Wikipédia en Français

  • Nombre réel — Pour les articles homonymes, voir Réel. En mathématiques, un nombre réel est un nombre qui peut être représenté par une partie entière et une liste finie ou infinie de décimales. Cette définition s applique donc aux nombres rationnels, dont les… …   Wikipédia en Français

  • Nombre calculable — Nombre réel calculable En informatique et algorithmique, un nombre réel calculable est un réel pour lequel il existe un algorithme ou une machine de Turing permettant d énumérer tous les chiffres de son développement décimal. Cette notion a été… …   Wikipédia en Français

  • Nombre incalculable — Nombre réel calculable En informatique et algorithmique, un nombre réel calculable est un réel pour lequel il existe un algorithme ou une machine de Turing permettant d énumérer tous les chiffres de son développement décimal. Cette notion a été… …   Wikipédia en Français

  • Nombre Normal — En mathématiques, un nombre normal est un nombre réel qui a ses chiffres équidistribués dans son développement décimal, ceux ci apparaissant tous à la même fréquence. Les « chiffres » font référence aux chiffres avant la virgule (la… …   Wikipédia en Français

  • Nombre+transcendant — Nombre transcendant En mathématiques, un nombre transcendant est un nombre réel ou complexe qui n est racine d aucune équation polynomiale : où et les coefficients sont des nombres entiers (donc des rationnels), dont au moins l un an est non …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”