- Calcul Intégral
-
Calcul intégral

Cet article fait partie de la série
Mathématiques élémentairesAlgèbre Logique Arithmétique Probabilités Statistiques Le calcul intégral est la deuxième des idées du calcul infinitésimal.
Sommaire
Primitives
Soit
 une fonction définie sur un intervalle
une fonction définie sur un intervalle  . Une fonction
. Une fonction  est une primitive de
est une primitive de  sur l’intervalle
sur l’intervalle  si
si  est dérivable sur
est dérivable sur  et si pour tout
et si pour tout 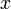 de
de  ,
, 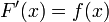 . Si
. Si  est une fonction continue sur un intervalle
est une fonction continue sur un intervalle  , alors il existe au moins une fonction
, alors il existe au moins une fonction  dérivable sur
dérivable sur  telle que
telle que  soit la dérivée de
soit la dérivée de  sur
sur  .
.  est alors une primitive de
est alors une primitive de  sur
sur  .
.Par exemple, si
 est définie sur
est définie sur  par
par 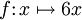 , alors la fonction
, alors la fonction  définie sur
définie sur 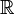 par
par 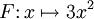 admet pour dérivée
admet pour dérivée  , et donc
, et donc  est une primitive de
est une primitive de  sur
sur 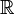 .
.Si
 est une primitive de
est une primitive de  sur
sur  , alors pour toute constante
, alors pour toute constante 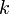 , la fonction
, la fonction 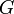 définie sur
définie sur  par
par 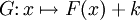 est aussi une primitive de
est aussi une primitive de  sur
sur  car la dérivée d'une application constante est la fonction nulle. Nous en déduisons que si
car la dérivée d'une application constante est la fonction nulle. Nous en déduisons que si  admet une primitive sur
admet une primitive sur  alors elle en admet une infinité.
alors elle en admet une infinité.Ensemble des primitives d’une fonction sur un intervalle
Deux primitives différentes d'une même fonction
 ne diffèrent que d'une constante. En effet si
ne diffèrent que d'une constante. En effet si  et
et 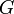 sont deux primitives de
sont deux primitives de  alors
alors 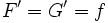 donc
donc 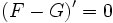 .
.  étant un intervalle, nous en déduisons qu’il existe
étant un intervalle, nous en déduisons qu’il existe 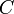 une constante définie sur telle que
une constante définie sur telle que 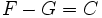 soit
soit 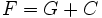
Soit
 une fonction définie sur un intervalle
une fonction définie sur un intervalle  . Si
. Si  admet une primitive
admet une primitive  sur
sur  , alors l'ensemble des primitives de
, alors l'ensemble des primitives de  sur
sur  est l'ensemble des fonctions
est l'ensemble des fonctions 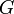 de la forme :
de la forme :où
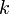 est une constante réelle. On remarque que les primitives de la fonction nulle sont les fonctions constantes.
est une constante réelle. On remarque que les primitives de la fonction nulle sont les fonctions constantes.Soit
 un intervalle,
un intervalle,  un réel de
un réel de  et
et 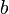 un réel quelconque. Il existe une et une seule primitive
un réel quelconque. Il existe une et une seule primitive  , d’une fonction
, d’une fonction  continue sur
continue sur  , telle que
, telle que  .
.  est appelée la primitive de
est appelée la primitive de  sur
sur  vérifiant la condition initiale :
vérifiant la condition initiale :  .
.Par exemple pour trouver la primitive de
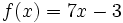 vérifiant la condition initiale
vérifiant la condition initiale 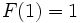 .
.On calcule d'abord la forme générale de la primitive
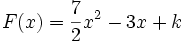 .
.Puis on résout l'équation
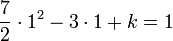 et on obtient
et on obtient 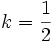 et donc la primitive recherchée est
et donc la primitive recherchée est 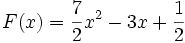 .
.Intégrale
Définition de l’intégrale à partir de la notion de primitive
Soit
 une fonction définie sur un intervalle
une fonction définie sur un intervalle  et admettant des primitives sur
et admettant des primitives sur  . Soient
. Soient  et
et 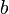 dans
dans  . Soit
. Soit  une primitive de
une primitive de  sur
sur  . Nous appelons intégrale de
. Nous appelons intégrale de  à
à 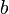 de
de  , le nombre :
, le nombre :qui ne dépend pas du choix de la primitive de
 , parce que les primitives de
, parce que les primitives de  sur l’intervalle
sur l’intervalle  diffèrent d’une fonction constante. Nous notons ce nombre :
diffèrent d’une fonction constante. Nous notons ce nombre :qui se lit « intégrale de
 à
à 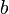 de
de  », et nous pouvons aussi le noter
», et nous pouvons aussi le noterqui se lit «
 . pris entre
. pris entre  . et
. et 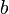 . »
. »Dans la notation avec le symbole de intégrale,
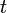 joue le rôle d’une variable muette, et nous avons
joue le rôle d’une variable muette, et nous avons-
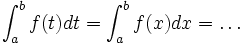 ,
,
de plus le nombre représenté par cette intégrale ne dépend pas de
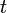 .
.Remarquons dans le cas où
 est continue sur
est continue sur  , que l’application
, que l’application 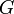 définie sur
définie sur  :
:n’est autre que la primitive de
 qui s’annule en
qui s’annule en  et cette fonction
et cette fonction 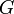 est donc la seule fonction dérivable sur
est donc la seule fonction dérivable sur  telle
telle 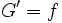 et
et 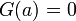 .
.Nous avons donc
Propriétés de l’intégrale
Linéarité de l'intégrale
Si
 et
et 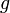 sont deux fonctions définies sur un intervalle
sont deux fonctions définies sur un intervalle  et admettant des primitives sur
et admettant des primitives sur  , alors la fonction
, alors la fonction 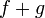 admet aussi des primitives sur
admet aussi des primitives sur  et pour tout
et pour tout  et tout
et tout 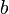 de
de  , on a :
, on a :De plus, si
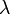 est un réel quelconque alors la fonction
est un réel quelconque alors la fonction  admet des primitives sur
admet des primitives sur  et :
et :Soient
 et
et 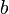 deux réels de l’intervalle
deux réels de l’intervalle  . Si
. Si  une fonction définie sur
une fonction définie sur  et admettant des primitives sur
et admettant des primitives sur  , alors pour tous
, alors pour tous  ,
, 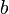 et
et  dans
dans 
 (relation de Chasles)
(relation de Chasles)
En effet si
 est une primitive de
est une primitive de  sur
sur  alors :
alors : .
.
En prenant
 dans la relation de Chasles, nous obtenons :
dans la relation de Chasles, nous obtenons :en effet
Positivité de l’intégrale
Soit
 une fonction définie sur l'intervalle
une fonction définie sur l'intervalle  qui admet des primitives sur
qui admet des primitives sur  , et si
, et si  et
et 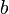 sont deux réels dans
sont deux réels dans  tels que
tels que 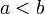 .
.Si pour tout réel
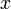 de
de ![\left [a, b \right ]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) ,
, 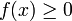 alors
alorsEn effet sous cette condition, toute primitive de
 sur l’intervalle
sur l’intervalle  est croissante.
est croissante.Conséquences :
Croissance de l’intégrale
Si
 et
et 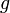 admettent des primitives sur
admettent des primitives sur  et si pour tout
et si pour tout 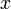 dans
dans ![\left[a, b \right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) ,
, 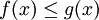 alors
alors(il suffit de poser
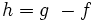 et d'utiliser la positivité et la linéarité de l’intégrale)
et d'utiliser la positivité et la linéarité de l’intégrale)Inégalité de la moyenne
S’il existe
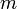 et
et  des réels tels que pour tout
des réels tels que pour tout 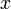 dans
dans ![\left[a, b\right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) ,
, 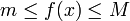 , alors
, alorsS’il existe un réel
 tel que pour tout
tel que pour tout 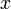 dans
dans ![\left[a, b\right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) ,
, 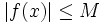 , alors
, alorsS’il existe un réel
 tel que pour tout
tel que pour tout 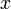 dans
dans  ,
, 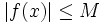 , alors pour tout
, alors pour tout  et tout
et tout 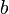 dans
dans  ,
,Forme simple du premier théorème de la moyenne
Si
 est continue sur
est continue sur  , alors pour tout
, alors pour tout  et tout
et tout 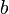 dans
dans  , il existe un réel
, il existe un réel  compris entre
compris entre  et
et 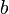 tel que :
tel que :Valeur moyenne d'une fonction
Si
 admet des primitives sur un intervalle
admet des primitives sur un intervalle  , si
, si  et
et 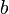 sont dans
sont dans  tels que
tels que  <
<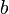 , nous appelons valeur moyenne de
, nous appelons valeur moyenne de  sur
sur ![\left[a, b\right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) , le nombre :
, le nombre :Parité
Soit
 une fonction qui admet des primitives sur un intervalle
une fonction qui admet des primitives sur un intervalle  centré en 0. Si
centré en 0. Si  est un réel, tel que
est un réel, tel que  et
et 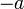 appartiennent à
appartiennent à  , alors:
, alors:- si
 est paire,
est paire, 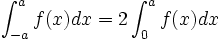
- si
 est impaire,
est impaire, 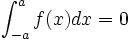
Intégrale et aire
Un cas particulier :
Soient
 et
et 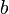 deux réels tels que
deux réels tels que 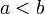 . Soit
. Soit  une fonction constante sur
une fonction constante sur ![\left[a, b\right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) et soit
et soit  tel que
tel que- pour tout réel
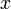 de
de ![\left[a, b\right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) ,
,  =
=
Alors l’intégrale de
 à
à 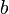 de
de  est égale à
est égale à 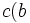 -
-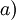 et représente l’aire algébrique du rectangle de sommets
et représente l’aire algébrique du rectangle de sommets 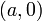 ,
, 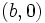 ,
, 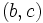 et
et 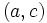 .
.Théorème :
Soient
 et
et 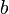 deux réels tels que
deux réels tels que 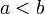 . Soit
. Soit  une fonction continue sur
une fonction continue sur ![\left[a, b\right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) . Soit
. Soit 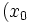 ,
, 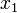 , …,
, …,  une suite strictement croissante de points partageant le segment
une suite strictement croissante de points partageant le segment ![\left[a, b\right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) en
en 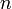 intervalles de longueur
intervalles de longueurNous avons alors pour tout
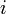 compris entre
compris entre 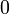 et
et 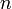 ,
,Alors la somme
tend vers
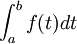 lorsque
lorsque 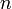 tend vers
tend vers 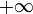 .
.Interprétation graphique :
Cette somme (appelée somme de Riemann) représente graphiquement la somme algébrique des aires des rectangles de gauche et est une valeur approchée de
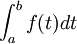 .
.Si
 est une fonction positive continue sur
est une fonction positive continue sur ![\left[a, b\right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) et si
et si  est la courbe représentative de
est la courbe représentative de  dans le plan rapporté à un repère orthogonal
dans le plan rapporté à un repère orthogonal 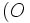 ;
; 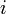 ,
,  ,
, 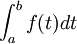 est la mesure de l’aire du plan délimité par
est la mesure de l’aire du plan délimité par 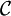 , l’axe des abscisses
, l’axe des abscisses 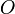
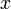 et les droites d’équations
et les droites d’équations 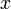 =
= et
et 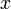 =
=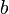 . L’unité d’aire étant l’aire du rectangle
. L’unité d’aire étant l’aire du rectangle 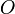

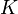
 .
.Méthodes de calcul d'une intégrale
Calcul direct à l'aide des primitives usuelles
Intégration par parties
Théorème :
Soit
 un intervalle. Soient
un intervalle. Soient  et
et 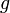 deux fonctions dérivables sur
deux fonctions dérivables sur  telles que les fonctions
telles que les fonctions 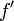
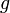 et
et 
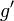 soient continues sur
soient continues sur  . Soit
. Soit  un réel dans
un réel dans  . Alors, pour tout réel
. Alors, pour tout réel 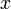 dans
dans 
En particulier :
Théorème :
Soient
 et
et 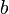 deux réels tels que
deux réels tels que 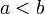 . Soient
. Soient  et
et 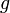 deux fonctions dérivables sur
deux fonctions dérivables sur ![\left[a, b\right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) et telles que les fonctions
et telles que les fonctions 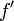 ,
, 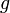 ,
,  et
et 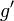 soient continues sur
soient continues sur ![\left[a, b\right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) . Alors :
. Alors :On peut généraliser cette formule aux fonctions de classe Ck + 1
Intégration par la méthode des résidus
Article détaillé : Théorème des résidus.Calcul numérique approché d'une intégrale
On considère ici le cas d'une fonction
 définie sur
définie sur ![\left [a, b \right ]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) . On définit le « pas » d'approximation
. On définit le « pas » d'approximation 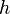 de la manière suivante :
de la manière suivante : 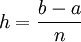 ; où
; où 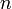 détermine la précision de l'approximation. On définit aussi
détermine la précision de l'approximation. On définit aussi 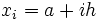 .
.Méthode des rectangles
La méthode des rectangles revient à une approximation de
 par une fonction en escalier, avec
par une fonction en escalier, avec 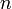 « marches » de longueur
« marches » de longueur 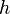 . La valeur approchée
. La valeur approchée 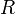 de l'intégrale vaut alors :
de l'intégrale vaut alors :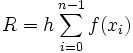 .
.Méthode des trapèzes
Article détaillé : Méthode des trapèzes.On utilise une fonction continue affine par morceaux approchant la fonction à intégrer et égale à celle-ci sur les points de la subdivision en
 sous-intervalles égaux de l'intervalle d'intégration
sous-intervalles égaux de l'intervalle d'intégration ![\left[ a , b \right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) pour obtenir une approximation de la valeur de son intégrale sur
pour obtenir une approximation de la valeur de son intégrale sur ![\left[ a , b \right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) .
.En remplaçant par des trapèzes les rectangles utilisés précédemment, on obtient :
![R = h\left[ \frac{f(a)+f(b)}{2} + \sum_{i=1}^{n-1} f(x_i) \right]\,](/pictures/frwiki/48/0ffc6152bf5247b20a232027c1e41f68.png) .
.
On peut déterminer la précision de cette approximation en utilisant la formule suivante :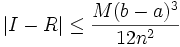 où
où  est la borne supérieure de la valeur absolue de la dérivée d'ordre 2 de
est la borne supérieure de la valeur absolue de la dérivée d'ordre 2 de  sur
sur ![[a;b]\,](/pictures/frwiki/100/d21f69511ca60f3abd84c78449fef37c.png) et
et  la valeur exacte de l'intégrale.
la valeur exacte de l'intégrale.Méthode de Simpson
Article détaillé : Méthode de Simpson.On utilise maintenant des paraboles que l'on fait passer par trois points consécutifs du découpage en
 segments de l'intervalle d'intégration de
segments de l'intervalle d'intégration de  .
.On s'appuie sur le résultat exact suivant où
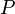 est une fonction polynomiale de degré deux :
est une fonction polynomiale de degré deux :Si
 ,
, 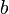 et
et  sont trois réels tels que
sont trois réels tels que 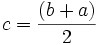 , alors
, alors 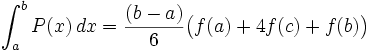 On obtient alors une valeur approchée de
On obtient alors une valeur approchée de  avec la formule suivante :
avec la formule suivante :![R = \frac{h}{6} \left[ f(a) + f(b) + 4 \sum_{i=0}^{n-1}f(x_{2i+1}) + 2 \sum_{i=1}^{n-1} f(x_{2i}) \right]\,](/pictures/frwiki/102/fe1bd66b54b764bcf17b0e3dd7211180.png) où
où 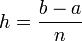 et
et 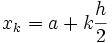
On peut ici aussi déterminer la précision de la méthode, avec la formule suivante :
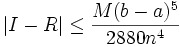 où
où  est la borne supérieure de la valeur absolue de la dérivée d'ordre 4 de
est la borne supérieure de la valeur absolue de la dérivée d'ordre 4 de  sur
sur ![[a;b]\,](/pictures/frwiki/100/d21f69511ca60f3abd84c78449fef37c.png) et
et  la valeur exacte de l'intégrale.
la valeur exacte de l'intégrale.Méthode de Gauss-Legendre
Article détaillé : Méthodes de quadrature de Gauss.On utilise aussi en analyse numérique une méthode basée sur l'orthogonalité des polynômes de Legendre. pour le produit scalaire
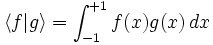
Elle est appelée méthode de Gauss-Legendre, et permet de calculer avec une grande précision les intégrales de fonctions suffisamment régulières sur un segment
![\left[ a , b \right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png)
Il suffit de réaliser une application affine de
![\left[ a , b \right]\,](/pictures/frwiki/51/306000b4d4732ac8ef6254abda3a9776.png) sur
sur ![\left[ -1 , +1 \right]\,](/pictures/frwiki/54/6033617927755bc39f68edd671632201.png) , et de remarquer que
, et de remarquer que
où
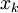 sont les racines du polynôme de Legendre de degré
sont les racines du polynôme de Legendre de degré 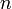
et où
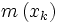 sont les poids de ces racines, qui sont tels que l'égalité
sont les poids de ces racines, qui sont tels que l'égalité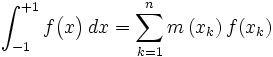 est assurée pour toute fonction polynomiale de degré inférieur ou égal à
est assurée pour toute fonction polynomiale de degré inférieur ou égal à 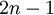
Les premiers polynômes sont
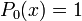
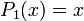
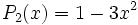
...
Une excellente précision est garantie dès que
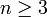 . Des tables permettent d'obtenir les valeurs des points et leurs poids.
. Des tables permettent d'obtenir les valeurs des points et leurs poids.Exemple
Tableau des valeurs pour 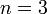
Numéro Abscisse Poids 1 
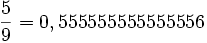
2 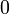
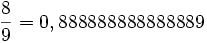
3 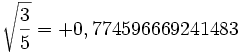
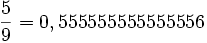
Voir aussi
- Intégrale
- Table d'intégrales
- Calcul intégral
- Calcul numérique d'une intégrale
- Primitive
- Règles de Bioche
- Portail des mathématiques
Catégories : Mathématiques élémentaires | Théorie de l'intégration
Wikimedia Foundation. 2010.


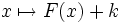
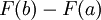
![\left[F(t)\right]_a^b\,](/pictures/frwiki/101/efb7211da49ec3eb321d68fcf9f62268.png)
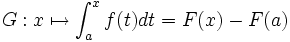
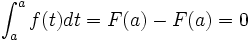
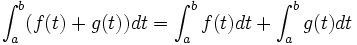
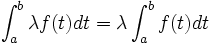
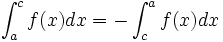
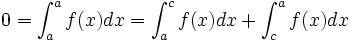

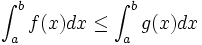
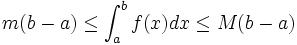
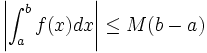
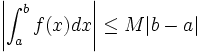
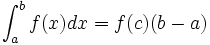
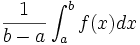
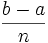
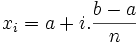
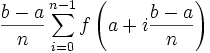
![\int_a^x f^{\prime}\left( t\right) g\left( t\right) dt=\left[f\left( t\right) g\left( t\right)\right]_a^x -\int_a^x f\left( t\right) g^{\prime }\left( t\right) dt\,](/pictures/frwiki/50/21825efec9933c343afb12a5ecb7d411.png)
![\int _{a}^{b}f^{\prime}\left( t\right) g\left( t\right) dt=\left[ f\left( t\right) g\left( t\right) \right] _{a}^{b}-\int _{a}^{b}f\left( t\right) g^{\prime }\left( t\right) dt\,](/pictures/frwiki/99/c03f613531c8737ed6b667815e26eb20.png)
![\int_{a}^{b} f^{(k+1)}(x) g(x)\,dx = \left[ \sum_{n=0}^{k}(-1)^{n} f^{(k-n)}(x) g^{(n)}(x) \right]_{a}^{b} + (-1)^{k+1} \int_{a}^{b} f(x) g^{(k+1)}(x) \,dx](/pictures/frwiki/48/05b1916578fd66de346deb9778646246.png)