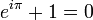Identite d'Euler
- Identite d'Euler
-
Identité d'Euler
En mathématiques, l'identité d'Euler est une relation mathématique, nommée ainsi en l'honneur du mathématicien Leonhard Euler.
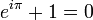
où  est la base du logarithme népérien,
est la base du logarithme népérien, 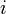 est l'unité des imaginaires purs (vérifiant
est l'unité des imaginaires purs (vérifiant 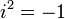 ) et
) et 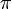 est la constante d'Archimède (le rapport de la circonférence d'un cercle à son diamètre).
est la constante d'Archimède (le rapport de la circonférence d'un cercle à son diamètre).
L'identité apparaît dans le livre Introductio de Leonhard Euler, publié à Lausanne en 1748.
Dans la préface de l'un de ses cahiers, alors qu'il avait presque quinze ans, Richard Feynman, qualifia cette identité de « formule la plus remarquable au monde ».[réf. nécessaire]
Cette formule est un cas particulier de la formule d'Euler en analyse complexe : pour tout nombre réel 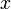 ,
, 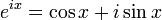 , qui est vrai en particulier pour
, qui est vrai en particulier pour  (or
(or 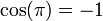 et
et 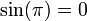 ).
).
Démonstration
|
|
|
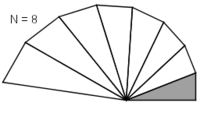
Juxtaposition de 8 triangles rectangles
|
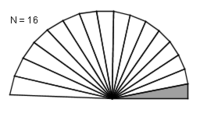
Juxtaposition de 16 triangles rectangles
|
|
|
 |
Cliquez sur une vignette pour l’agrandir |
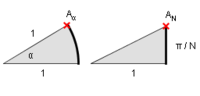
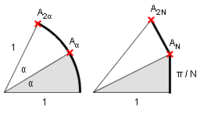
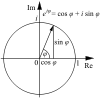
L'interprétation géométrique qui fournit une piste de démonstration par une suite est basée sur la juxtaposition de triangles rectangles.
- Pour tout
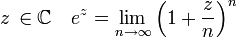
Or les multiplications complexes se traduisant par des rotations, le point de coordonnées 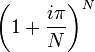 est obtenu en juxtaposant N triangles rectangles.
est obtenu en juxtaposant N triangles rectangles.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Analyse complexe | Exponentielle | Identité mathématique | Théorème de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Identite d'Euler de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Identité d'Euler — En mathématiques, l identité d Euler est une relation mathématique, nommée ainsi en l honneur du mathématicien Leonhard Euler. où est la base du logarithme népérien, est l unité des imaginaires purs (vérifiant ) et est la con … Wikipédia en Français
Identite (mathematiques) — Identité (mathématiques) Pour les articles homonymes, voir identité. Ne doit pas être confondu avec égalité (mathématiques) ou équation. En mathématiques et plus généralement dans les domaines scientifiques, une identité est la constatation … Wikipédia en Français
Euler — Leonhard Euler « Euler » redirige ici. Pour les autres significations, voir Euler (homonymie). Leonhard Euler … Wikipédia en Français
Identité (mathématiques) — Pour les articles homonymes, voir identité. Ne doit pas être confondu avec égalité (mathématiques) ni équation. En mathématiques et plus généralement dans les domaines scientifiques, une identité est la constatation que deux objets… … Wikipédia en Français
Identite remarquable (mathematiques elementaires) — Identité remarquable Pour les articles homonymes, voir Identité. En mathématiques, on appelle identités remarquables ou encore égalités remarquables certaines égalités qui s appliquent à des nombres. Elles servent en général à accélérer les… … Wikipédia en Français
Identite trigonometrique — Identité trigonométrique Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une… … Wikipédia en Français
Identité Trigonométrique — Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une expression comportant des… … Wikipédia en Français
Identité remarquable (maths élém) — Identité remarquable Pour les articles homonymes, voir Identité. En mathématiques, on appelle identités remarquables ou encore égalités remarquables certaines égalités qui s appliquent à des nombres. Elles servent en général à accélérer les… … Wikipédia en Français
Identité remarquable (mathématiques élémentaires) — Identité remarquable Pour les articles homonymes, voir Identité. En mathématiques, on appelle identités remarquables ou encore égalités remarquables certaines égalités qui s appliquent à des nombres. Elles servent en général à accélérer les… … Wikipédia en Français
Identite des quatre carres d'Euler — Identité des quatre carrés d Euler En mathématiques, l identité des quatre carrés d Euler énonce que le produit de deux nombres, chacun étant la somme de quatre carrés, est lui même une somme de quatre carrés. Précisément … Wikipédia en Français
 est la base du logarithme népérien,
est la base du logarithme népérien, 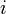 est l'unité des imaginaires purs (vérifiant
est l'unité des imaginaires purs (vérifiant 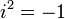 ) et
) et 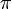 est la constante d'Archimède (le rapport de la circonférence d'un cercle à son diamètre).
est la constante d'Archimède (le rapport de la circonférence d'un cercle à son diamètre).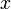 ,
, 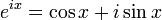 , qui est vrai en particulier pour
, qui est vrai en particulier pour  (or
(or 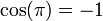 et
et 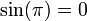 ).
).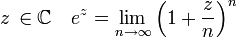
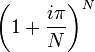 est obtenu en juxtaposant N triangles rectangles.
est obtenu en juxtaposant N triangles rectangles.