De la mesure du cercle

De la mesure du cercle

De la mesure du cercle (grec ancien : Κύκλου μέτρησις, Kuklou metrēsis) est un traité d'Archimède composé de trois propositions. Ce traité est seulement une partie de ce qui était une œuvre plus importante[1],[2].

Sommaire

Propositions

Proposition une

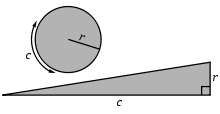
Le cercle et le triangle ont la même aire.

Tout cercle équivaut au triangle rectangle pour lequel on a le rayon égal à l'un des côtés adjacents à l'angle droit et le périmètre égal à la base.

Tout cercle de circonférence c et de rayon r est de même aire qu'un triangle rectangle de cathètes c et r. Cette proposition peut se prouver par exhaustion[3].

Proposition deux

Le rapport de la surface du cercle au carré de son diamètre est celui de 11 à 14.

Autrement dit, 22/7 est une bonne approximation du nombre pi.


Proposition trois

Exemples de la manière dont Archimède calcule π. Archimède utilise un polygone de 96 côtés pour son approximation.

Le rapport entre la circonférence d'un cercle et son diamètre est inférieur à 3 + \tfrac{10}{70} mais supérieur à 3 + \tfrac{10}{71}.

Cette proposition revient à fournir un encadrement au nombre π. Archimède a trouvé des majorants et minorants de π en inscrivant et en circonscrivant un cercle à deux polygones réguliers similaires de 96 côtés[4].

Approximation de racines carrées

Cette proposition contient aussi une approximation supérieure et inférieure de √3 et d'autres approximations supérieures de racines carrées.

\tfrac{1351}{780} > \sqrt{3} > \tfrac{265}{153}\,.[3]

Cependant Archimède ne donne pas d'explications sur la manière d'obtenir ces approximations[2].

Sources

Liens externes

Références

  1. ↑ (en) Thomas Heath, « A History of Greek Mathematics », (ISBN 0543968774). Consulté le 30 juin 2008
  2. ↑ a et b (en) Archimede, Encyclopædia Britannica, 2008. Consulté le 30 juin 2008
  3. ↑ a et b (en) Thomas Little Heath, « The Works of Archimedes », Cambridge University, 1897, p. lxxvii ; 50. Consulté le 30 juin 2008
  4. ↑ (en) Thomas Little Heath, « A Manual of Greek Mathematics », Cambridge University, 1931, (ISBN 0486432319), p. 146. Consulté le 30 juin 2008

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article De la mesure du cercle de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • MESURE (musique) — Une œuvre musicale s’inscrit dans le temps, et la musique est un art temporel; l’importance de la perception du temps en musique se comprend aisément si l’on fait une comparaison avec les arts plastiques. En regardant un tableau, on a la… …   Encyclopédie Universelle

  • cercle — [ sɛrkl ] n. m. • 1160 « objet circulaire »; lat. circulus, de circus « cercle » I ♦ 1 ♦ Courbe plane fermée dont tous les points sont à égale distance R (⇒ 1. rayon) d un centre. Circonférence d un cercle, égale à 2 π R. Diamètre d un cercle :… …   Encyclopédie Universelle

  • Cercle Trigonométrique — Dans le plan euclidien muni d un repère orthonormé, le cercle trigonométrique, ou cercle unité, est le cercle dont le rayon est égal à 1 et qui est centré sur l origine du repère. Fonctions trigonométriques sur le cercle …   Wikipédia en Français

  • Cercle Unité — Cercle trigonométrique Dans le plan euclidien muni d un repère orthonormé, le cercle trigonométrique, ou cercle unité, est le cercle dont le rayon est égal à 1 et qui est centré sur l origine du repère. Fonctions trigonométriques sur le cercle …   Wikipédia en Français

  • Cercle trigonometrique — Cercle trigonométrique Dans le plan euclidien muni d un repère orthonormé, le cercle trigonométrique, ou cercle unité, est le cercle dont le rayon est égal à 1 et qui est centré sur l origine du repère. Fonctions trigonométriques sur le cercle …   Wikipédia en Français

  • MESURE — DÈS qu’un phénomène d’apparence bien définie est justiciable d’une quantification, de manière répétable et suffisamment précise, il est considéré comme une grandeur . On peut caractériser son état ou son intensité par un nombre ou valeur et faire …   Encyclopédie Universelle

  • MESURE - Mesures électriques et électroniques — Les mesures électriques et électroniques, grâce à l’apport des semiconducteurs, des méthodes numériques et des systèmes asservis, apparaissent à l’heure actuelle comme une technique clé dans le domaine des mesures en général. L’existence de… …   Encyclopédie Universelle

  • Cercle Circassien — Le cercle circassien (en anglais Circassian Circle) est une danse originaire d Écosse (comté de Lanarkshire), apparue à la fin du XIXe siècle et que l on danse aujourd hui dans les bals folk sur un air de gigue. On ignore l origine du nom et …   Wikipédia en Français

  • MESURE - Mesures mécaniques — On rassemble généralement sous le vocable «mesures mécaniques» l’examen des moyens et des techniques de mesure des grandeurs qui interviennent dans l’étude du fonctionnement d’une machine. Ces grandeurs sont nombreuses et fort diverses, mais leur …   Encyclopédie Universelle

  • Mesure Des Distances En Astronomie — Plusieurs méthodes ont été identifiées pour mesurer des distances en astronomie. Chaque méthode n est applicable que pour une certaine échelle. Le recoupement des méthodes permet, de proche en proche, de mesurer la distance des objets les plus… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”