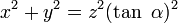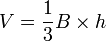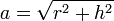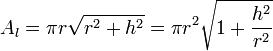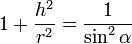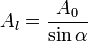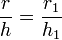Cône (Géométrie)

Cône (géométrie)

Pour les articles homonymes, voir Cône.

En géométrie, un cône désigne ou bien une surface réglée ou bien un solide

Sommaire

1 Surface
2 Solide
3 Voir aussi
- 3.1 Articles connexes
- 3.2 Liens externes

Surface

Cas général

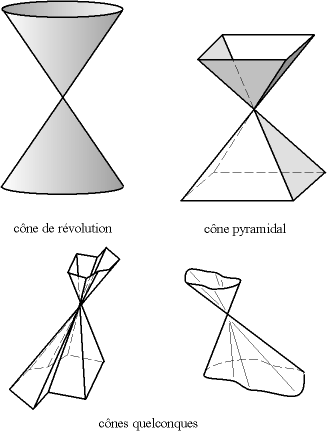
Un cône est une surface réglée définie par une droite (d), appelée génératrice, passant par un point fixe S appelé sommet et un point variable décrivant une courbe plane fermée (c), appelée courbe directrice.

On parle aussi dans ce cas de surface conique.

Cône de révolution

Parmi ces surfaces coniques, la plus étudiée est le cône de révolution dans lequel la courbe directrice est un cercle de centre O situé dans un plan perpendiculaire à (SO). Ce cône est appelé de révolution car il peut être généré simplement par la rotation d'une droite (d) passant par S autour d'un axe (Sz) différent de (d). La génératrice du cône fait alors un angle fixe $a$ avec l'axe de rotation.

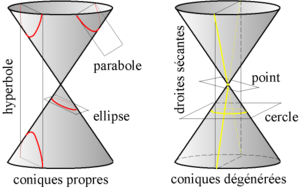
C'est à partir de ce cône de révolution que les mathématiciens (dont Apollonius de Perga) ont classifié un ensemble de courbes comme des coniques (intersection du cône et d'un plan) : cercles, ellipses, paraboles, hyperboles.

Dans le repère orthonormal (S, i, j, k), l'équation du cône de révolution d'axe (Sz) et de sommet S est donnée par :

$x^2+y^2=z^2(\tan\ \alpha)^2$

où $α$ est l'angle du cône, formé par l'axe et une génératrice.

Sections d'un cône de révolution par un plan

Intersection d'un plan et d'un cône de révolution

Dans les cas où le plan est parallèle ou perpendiculaire à l'axe de révolution du cône on obtient les courbes suivantes :

La section d'un cône de révolution par un plan perpendiculaire à l'axe de révolution est un cercle.
La section d'un cône de révolution par un plan parallèle à l'axe de révolution est
- l'union de deux droites sécantes si le plan contient l'axe de révolution
- une hyperbole dans le cas contraire

Plus généralement , la section d'un cône de révolution par un plan donne une conique. Ainsi on trouve,

une parabole (réduite éventuellement à une génératrice) lorsque le plan est strictement parallèle à une génératrice du cône
une ellipse (éventuellement réduite à un point) quand l'angle que forme le vecteur normal au plan et l'axe de rotation est inférieur à π/2 - α
une hyperbole (éventuellement réduite à deux droites sécantes) quand l'angle que forme le vecteur normal au plan et l'axe de rotation est isupérieur à π/2 - α

Solide

Cas général

cône de révolution et cône quelconque

On appelle aussi cône le solide délimité par la surface conique , le sommet S et un plan (P) ne contenant pas S et sécant à toutes les génératrices. La section du plan et de la surface s'appelle la base du cône.

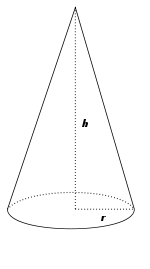
Lorsque la section est circulaire de centre O et que la droite (OS) est perpendiculaire à la section, le cône est appelé cône de révolution ou cône circulaire droit. C'est le cône le plus connu (cornet de glace, chapeau de clown). Dans ce cas, la distance séparant le sommet d'un point quelconque du cercle est constante et s'appelle l'apothème du cône.

Lorsque la courbe fermée est un polygone, on obtient une pyramide.

Quelle que soit la forme du cône, son volume est toujours

$V = \frac{1}{3}B\times h$

où $B$ est la surface de la base et $h$ la hauteur du cône, c'est-à-dire la distance séparant le sommet S et le plan (P)

Cas du cône de révolution

cône de révolution

Dans le cas particulier du cône de révolution, les formules du volume V et de l'aire A (aire de la surface enfermant le cône: aire latérale + base circulaire) sont

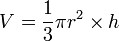
$V = \frac{1}{3}\pi r^2\times h$

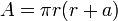$A = \pi r (r+a)\,$ ,

où r est le rayon du cercle de base, h la hauteur du cône et

$a = \sqrt{r^2 + h^2}$

l'apothème du cône.

L'aire latérale A_l (sans la base) vaut

$A_l = \pi r \sqrt{r^2 + h^2} = \pi r^2 \sqrt{1 + \frac{h^2}{r^2}}$

or, d'après les relations trigonométriques dans le triangle rectangle, on a

$1 + \frac{h^2}{r^2} = \frac{1}{\sin ^2\alpha}$

où α est le demi-angle au sommet. Si A₀ est l'aire de la base π⋅r ², on a alors

$A_l = \frac{A_0}{\sin \alpha}$

Cette formule sert par exemple à calculer l'aire du front de flamme dans le cas d'une flamme conique, donc la consommation de gaz et la puissance de cette flamme.

Section du cône de révolution par un plan

Quand on coupe un solide, cône de révolution, par un plan parallèle à la base, on obtient un cercle. Le rayon r₁ de ce cercle s'obtient en fonction du rayon r de la base, de la hauteur h du cône et de la distance h₁ entre le plan et le sommet du cône en utilisant le théorème de Thalès :

$\frac{r}{h}=\frac{r_1}{h_1}$

Quand on coupe ce même cône par un plan contenant son axe de révolution , on obtient un triangle isocèle de base 2r et de hauteur h.

Patron ou développement d'un cône de révolution

Développement du cône de révolution

Pour obtenir le patron d'un cône de révolution de rayon r et de hauteur h, il faut d'abord calculer l'apothème

$a=\sqrt{r^2+h^2}$

Il suffit alors de tracer un cercle de rayon r et une portion de cercle de rayon a dont l'angle au centre vaut 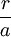$\frac{r}{a}$ de l'angle plein.

Voir aussi

Liens externes

A. Javary, Traité de géométrie descriptive, 1881 (sur Gallica) : Cônes et cylindres, sphère et surfaces du second degré

Solides géométriques
Les polyèdres
Les solides de Platon
Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre
Les solides d'Archimède
Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre
Les solides de Kepler-Poinsot
Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre
Les solides de Catalan
Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre
Les solides de Johnson
Les solides de révolution
Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution

Portail de la géométrie

Ce document provient de « C%C3%B4ne (g%C3%A9om%C3%A9trie) ».

Catégories : Surface | Surface réglée

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Cône (Géométrie) de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Cône (géométrie) — Pour les articles homonymes, voir Cône. En géométrie, un cône désigne une surface réglée ou bien un solide Sommaire 1 Surface 1.1 Cas général … Wikipédia en Français
Cône (solide) — Cône (géométrie) Pour les articles homonymes, voir Cône. En géométrie, un cône désigne ou bien une surface réglée ou bien un solide Sommaire 1 Surface 1.1 Cas général … Wikipédia en Français
Cone — Cône Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Cône (forme) — Cône Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Geometrie analytique — Géométrie analytique La géométrie analytique est une approche de la géométrie dans laquelle les objets sont représentés par des équations ou des inéquations. Elle est fondamentale pour la physique et l infographie. En géométrie analytique le… … Wikipédia en Français
Géométrie Analytique — La géométrie analytique est une approche de la géométrie dans laquelle les objets sont représentés par des équations ou des inéquations. Elle est fondamentale pour la physique et l infographie. En géométrie analytique le choix d un repère est… … Wikipédia en Français
Géométrie analytique — La géométrie analytique est une approche de la géométrie dans laquelle les objets sont représentés par des équations ou des inéquations. Elle est fondamentale pour la physique et l infographie. En géométrie analytique le choix d un repère est… … Wikipédia en Français
GÉOMÉTRIE — La géométrie est communément définie comme la science des figures de l’espace. Cette définition un peu incertaine risque de conduire à inclure dans la géométrie des questions qui ne sont géométriques que dans leur langage, mais relèvent en fait… … Encyclopédie Universelle
Geometrie euclidienne — Géométrie euclidienne Euclide. La géométrie euclidienne commence avec les Éléments d Euclide, qui est à la fois une somme des connaissances géométriques de l époque et une tentative de formalisation mathématique de ces connaissances. Les notions… … Wikipédia en Français
Géométrie Euclidienne — Euclide. La géométrie euclidienne commence avec les Éléments d Euclide, qui est à la fois une somme des connaissances géométriques de l époque et une tentative de formalisation mathématique de ces connaissances. Les notions de droite, de plan, de … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Cône (Géométrie)