Liste des polyèdres uniformes

Liste des polyèdres uniformes: Cette liste recense les polyèdres uniformes, ainsi que certaines de leurs propriétés.

Sommaire

1 Méthodologie

2 Table des polyèdres

2.1 Formes convexes (3 faces/sommet)

2.2 Formes convexes (4 faces/sommet)

2.3 Formes convexes (5 faces/sommet)

2.4 Formes non convexes avec des faces convexes

2.5 Formes prismatiques non convexes

2.6 Autres formes non convexes avec des faces non convexes

2.7 Cas particulier

3 Renvois

4 Liens externes

Méthodologie

Un polyèdre uniforme est un polygone dont les faces sont des polygones réguliers et qui est isogonal (c'est-à-dire que pour tout couple de ses sommets, il existe une isométrie du polyèdre qui transforme l'un en l'autre).

Les polyèdres uniformes suivants existent :

75 polyèdres uniformes non prismatiques :

18 polyèdres convexes :

5 solides de Platon, réguliers ;

13 solides d'Archimède :

2 polyèdres quasi-réguliers ;

11 polyèdres semi-réguliers ;

57 polyèdres étoilés :

4 solides de Kepler-Poinsot, réguliers ;

5 polyèdres étoilés quasi-réguliers ;

48 polyèdres semi-réguliers ;

le grand dirhombidodécaèdre disadouci, polyèdre particulier dont certaines paires d'arêtes coïncident ;

les ensembles infinis :

prismes uniformes, convexes et étoilés ;

antiprismes uniformes, convexes et étoilés.

La liste inclut, les 76 polyèdres précédents, ansi que quelques exemples de prismes et d'antiprismes.

Elle n'inclut par les éléments suivants :

les 40 polyèdres uniformes potentiels avec des figures de sommet dégénérées qui ont des arêtes qui se chevauchent (non comptés par Coxeter) ;

les pavages uniformes :

les 11 pavages uniformes avec des faces convexes ;

les 14 pavages uniformes avec des faces non convexes;

l'ensemble infini des pavages hyperboliques uniformes.

Table des polyèdres

Les formes convexes sont listées en ordre de degrés de configuration de sommet à partir de 3 faces/sommet et au-dessus, et en augmentant les côtés par face. Cet ordre permet de montrer des similarités topologiques.

Formes convexes (3 faces/sommet)

Nom Image Classe de solide Symbole de Wythoff Figure de sommet Acronyme de Bowers Groupe de symétrie W# U# K# Sommets Arêtes Faces χ Faces par type

Tétraèdre R 2 3
3.3.3 Tet {3}

Prisme triangulaire P 2
3.4.4 Trip D_3h — — — 6 9 5 2 2××{3}+3×{4}

Tétraèdre tronqué 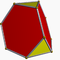A 3
3.6.6 Tut {3}+4×{6}

Cube tronqué A 4
3.8.8 Tic {3}+6×{8}

Dodécaèdre tronqué 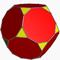A 5
3.10.10 Tid {3}+12×{10}

Cube R 2 4
4.4.4 Cube {4}

Prisme pentagonal P 2
4.4.5 Pip D_5h — U76 K01 10 15 7 2 5×{4}+2×{5}

Prisme hexagonal 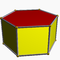P 2
4.4.6 Hip D_6h — — — 12 18 8 2 6×{4}+2×{6}

Prisme octogonal 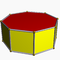P 2
4.4.8 Op D_8h — — — 16 24 10 2 8×{4}+2×{8}

Prisme décagonal 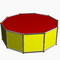P 2
4.4.10 Dip D_10h — — — 20 30 12 2 10×{4}+2×{10}

Prisme dodécagonal 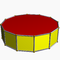P 2
4.4.12 Twip D_12h — — — 24 36 14 2 12×{4}+2×{12}

Octaèdre tronqué 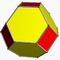A 3
4.6.6 Toe {4}+8×{6}

Cuboctaèdre tronqué A
4.6.8 Girco {4}+8×{6}+6×{8}

Icosidodécaèdre tronqué A
4.6.10 Grid {4}+20×{6}+12×{10}

Dodécaèdre 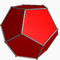R 2 5
5.5.5 Doe {5}

Icosaèdre tronqué A 3
5.6.6 Ti {5}+20×{6}

Formes convexes (4 faces/sommet)

Nom Image Classe de solide Symbole de Wythoff Figure de sommet Acronyme de Bowers Groupe de symétrie W# U# K# Sommets Arêtes Faces χ Faces par type

Octaèdre R 2 3
3.3.3.3 Oct {3}

Antiprisme carré P 2 2 4
3.3.3.4 Squap D_4d -- -- -- 8 16 10 2 8×{3}+2×{4}

Antiprisme pentagonal 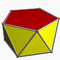P 2 2 5
3.3.3.5 Pap D_5d -- U77 K02 10 20 12 2 10×{3}+2×{5}

Antiprisme hexagonal 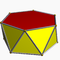P 2 2 6
3.3.3.6 Hap D_6d -- -- -- 12 24 14 2 12×{3}+2×{6}

Antiprisme octogonal 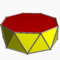P 2 2 8
3.3.3.8 Oap D_8d -- -- -- 16 32 18 2 16×{3}+2×{8}

Antiprisme décagonal 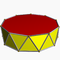P 2 2 10
3.3.3.10 Dap D_10d -- -- -- 20 40 22 2 20×{3}+2×{10}

Antiprisme dodécagonal 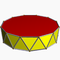P 2 2 12
3.3.3.12 Twap D_12d -- -- -- 24 48 26 2 24×{3}+2×{12}

Cuboctaèdre A 3 4
3.4.3.4 Co {3}+6×{4}

Petit rhombicuboctaèdre A 2
3.4.4.4 Sirco {3}+(6+12)×{4}

Petit rhombicosidodécaèdre A 2
3.4.5.4 Srid {3}+30×{4}+12×{5}

Icosidodécaèdre A 3 5
3.5.3.5 Id {3}+12×{5}

Formes convexes (5 faces/sommet)

Nom Image Classe de solide Symbole de Wythoff Figure de sommet Acronyme de Bowers Groupe de symétrie W# U# K# Sommets Arêtes Faces χ Faces par type

Icosaèdre R 2 3
3.3.3.3.3 Ike {3}

Cube adouci A 2 3 4
3.3.3.3.4 Snic O W017 U12 K17 24 60 38 2 (8+24)×{3}+6×{4}

Dodécaèdre adouci A 2 3 5
3.3.3.3.5 Snid I W018 U29 K34 60 150 92 2 (20+60)×{3}+12×{5}

Formes non convexes avec des faces convexes

Nom Image Classe de solide Symbole de Wythoff Figure de sommet Acronyme de Bowers Groupe de symétrie W# U# K# Sommets Arêtes Faces χ Faces par type

Tétrahémihexaèdre C+ 2
4.³/₂.4.3 Thah {3}+3×{4}

Cubohémioctaèdre C+ 3
6.⁴/₃.6.4 Cho {4}+4×{6}

Octahémioctaèdre C+ 3
6.³/₂.6.3 Oho {3}+4×{6}

Grand dodécaèdre R+ 2 5
(5.5.5.5.5)/₂ Gad {5}

Grand icosaèdre R+ 2 3
(3.3.3.3.3)/₂ Gike {3}

Grand icosidodécaèdre ditrigonal C+ 3 5
(5.3.5.3.5.3)/₂ Gidtid {3}+12×{5}

Petit rhombihexaèdre C+
4.8.⁴/₃.8 Sroh {4}+6×{8}

Petit cubicuboctaèdre C+ 4
8.³/₂.8.4 Socco {3}+6×{4}+6×{8}

Grand rhombicuboctaèdre uniforme C+ 2
4.³/₂.4.4 Querco {3}+(6+12)×{4}

Petit dodécahémidodécaèdre C+ 5
10.⁵/₄.10.5 Sidhid {5}+6×{10}

Petit icosihémidodécaèdre C+ 5
10.³/₂.10.3 Seihid {3}+6×{10}

Petit dodécicosaèdre C+
10.6.¹⁰/₉.⁶/₅ Siddy {6}+12×{10}

Petit rhombidodécaèdre C+
10.4.¹⁰/₉.⁴/₃ Sird {4}+12×{10}

Petit dodécicosidodécaèdre C+ 5
10.³/₂.10.5 Saddid {3}+12×{5}+12×{10}

Rhombicosaèdre C+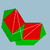
6.4.⁶/₅.⁴/₃ Ri {4}+20×{6}

Grand icosicosidodécaèdre C+ 3
6.³/₂.6.5 Giid {3}+12×{5}+20×{6}

Formes prismatiques non convexes

Nom Image Classe de solide Symbole de Wythoff Figure de sommet Acronyme de Bowers Groupe de symétrie W# U# K# Sommets Arêtes Faces χ Faces par type

Prisme pentagrammique P+ 2
⁵/₂.4.4 Stip D_5h -- U78 K03 10 15 7 2 5×{4}+2{⁵/₂}

Prisme heptagrammique (7/3) P+ 2
⁷/₃.4.4 Giship D_7h -- -- -- 14 21 9 2 7×{4}+2{⁷/₃}

Prisme heptagrammique (7/2) P+ 2
⁷/₂.4.4 Ship D_7h -- -- -- 14 21 9 2 7×{4}+2{⁷/₂}

Antiprisme pentagrammique P+ 2 2⁵/₂
⁵/₂.3.3.3 Stap D_5h -- U79 K04 10 20 12 2 10×{3}+2{⁵/₂}

Antiprisme pentagrammique croisé P+ 2 2⁵/₃
⁵/₃.3.3.3 Starp D_5d -- U80 K05 10 20 12 2 10×{3}+2{⁵/₂}

Autres formes non convexes avec des faces non convexes

Nom Image Classe de solide Symbole de Wythoff Figure de sommet Acronyme de Bowers Groupe de symétrie W# U# K# Sommets Arêtes Faces χ Faces par type

Petit dodécaèdre étoilé R+ 2⁵/₂
(⁵/₂)⁵ Sissid Grand dodécaèdre étoilé R+ 2⁵/₂
(⁵/₂)³ Gissid Dodécadodécaèdre ditrigonal S+ ⁵/₃ 5
(⁵/₃.5)³ Ditdid {5}+12{⁵/₂}

Petit icosidodécaèdre ditrigonal S+ ⁵/₂ 3
(⁵/₂.3)³ Sidtid {3}+12{⁵/₂}

Hexaèdre tronqué étoilé S+ ⁴/₃
⁸/₃.⁸/₃.3 Quith {3}+6{Grand rhombihexaèdre S+
4.⁸/₃.⁴/₃.⁸/₅ Groh {4}+6{Grand cubicuboctaèdre S+ ⁴/₃
⁸/₃.3.⁸/₃.4 Gocco {3}+6×{4}+6{Grand dodécahémidodécaèdre S+ ⁵/₃
¹⁰/₃.⁵/₃.¹⁰/₃.⁵/₂ Gidhid Petit dodécahémicosaèdre S+ 3
6.⁵/₃.6.⁵/₂ Sidhei {6}

Grand dodécahémicosaèdre S+ 3
6.⁵/₄.6.5 Gidhei {5}+10×{6}

Dodécadodécaèdre S+ ⁵/₂ 5
(⁵/₂.5)² Did {5}+12{⁵/₂}

Grand icosihémidodécaèdre S+ ⁵/₃
¹⁰/₃.³/₂.¹⁰/₃.3 Geihid {3}+6{Grand icosidodécaèdre S+ ⁵/₂ 3
(⁵/₂.3)² Gid {3}+12{⁵/₂}

Cuboctaèdre cubitronqué S+
⁸/₃.6.8 Cotco {6}+6×{8}+6{Grand cuboctaèdre tronqué S+
⁸/₃.4.6 Quitco {4}+8×{6}+6{Grand dodécaèdre tronqué 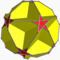S+ 5
10.10.⁵/₂ Tigid {10}

Petit dodécaèdre étoilé tronqué S+ ⁵/₃
¹⁰/₃.¹⁰/₃.5 Quitsissid {5}+12{Grand dodécaèdre étoilé tronqué S+ ⁵/₃
¹⁰/₃.¹⁰/₃.3 Quitgissid {3}+12{Grand icosaèdre tronqué S+ 3
6.6.⁵/₂ Tiggy {6}

Grand dodécicosaèdre S+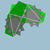
6.¹⁰/₃.⁶/₅.¹⁰/₇ Giddy {6}+12{Grand rhombidodécaèdre S+
4.¹⁰/₃.⁴/₃.¹⁰/₇ Gird {4}+12{Icosidodécadodécaèdre S+ 3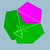
6.⁵/₃.6.5 Ided {5}+12{⁵/₂}+20×{6}

Petit dodécicosidodécaèdre ditrigonal 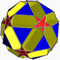S+ 5
10.⁵/₃.10.3 Sidditdid {3}+12{⁵/₂}+12×{10}

Grand dodécicosidodécaèdre ditrigonal S+ ⁵/₃
¹⁰/₃.3.¹⁰/₃.5 Gidditdid {3}+12×{5}+12{Grand dodécicosidodécaèdre S+ ⁵/₃
¹⁰/₃.⁵/₂.¹⁰/₃.3 Gaddid {3}+12{⁵/₂}+12{Petit icosicosidodécaèdre S+ 3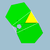
6.⁵/₂.6.3 Siid {3}+12{⁵/₂}+20×{6}

Rhombidodécadodécaèdre S+ 2
4.⁵/₂.4.5 Raded {4}+12×{5}+12{⁵/₂}

Grand rhombicosidodécaèdre uniforme S+ 2
4.⁵/₃.4.3 Qrid {3}+30×{4}+12{⁵/₂}

Dodécadodécaèdre adouci S+ 2⁵/₂ 5
3.3.⁵/₂.3.5 Siddid I W111 U40 K45 60 150 84 -6 60×{3}+12×{5}+12{⁵/₂}

Dodécadodécaèdre adouci inversé S+ ⁵/₃ 2 5
3.⁵/₃.3.3.5 Isdid I W114 U60 K65 60 150 84 -6 60×{3}+12×{5}+12{⁵/₂}

Grand icosidodécaèdre adouci S+ 2⁵/₂ 3
3.⁴.⁵/₂ Gosid I W116 U57 K62 60 150 92 2 (20+60)×{3}+12{⁵/₂}

Grand icosidodécaèdre adouci inversé S+ ⁵/₃ 2 3
3.³.⁵/₃ Gisid I W113 U69 K74 60 150 92 2 (20+60)×{3}+12{⁵/₂}

Grand icosidodécaèdre rétroadouci S+ ³/₂⁵/₃ 2
(3⁴.⁵/₂)/₂ Girsid I W117 U74 K79 60 150 92 2 (20+60)×{3}+12{⁵/₂}

Grand dodécicosidodécaèdre adouci S+ ⁵/₃⁵/₂ 3
3³.⁵/₃.3.⁵/₂ Gisdid I W115 U64 K69 60 180 104 -16 (20+60)×{3}+(12+12){⁵/₂}

Icosidodécadodécaèdre adouci S+ ⁵/₃ 3 5
3.³.5.⁵/₃ Sided I W112 U46 K51 60 180 104 -16 (20+60)×{3}+12×{5}+12{⁵/₂}

Petit icosicosidodécaèdre adouci S+ ⁵/₂ 3 3
3⁵.⁵/₂ Seside {3}+12{⁵/₂}

Petit icosicosidodécaèdre rétroadouci S+ ³/₂³/₂⁵/₂
(3⁵.⁵/₃)/₂ Sirsid {3}+12{⁵/₂}

Grand dirhombicosidodécaèdre S+ ³/₂⁵/₃ 3
⁵/₂

(4.⁵/₃.4.3.
4.⁵/₂.4.³/₂)/₂ Gidrid {3}+60×{4}+24{⁵/₂}

Dodécadodécaèdre icositronqué 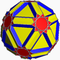S+
¹⁰/₃.6.10 Idtid {6}+12×{10}+12{Dodécadodécaèdre tronqué S+
¹⁰/₃.4.10 Quitdid {4}+12×{10}+12{Grand icosidodécaèdre tronqué S+
¹⁰/₃.4.6 Gaquatid {4}+20×{6}+12{modifier] Cas particulier

Nom Image Classe de solide Symbole de Wythoff Figure de sommet Acronyme de Bowers Groupe de symétrie W# U# K# Sommets Arêtes Faces χ Faces par type

Grand dirhombidodécaèdre disadouci
Polyèdre de Skilling S++ (3/2) 5/3 (3) 5/2
(⁵/₂.4.3.3.3.4.⁵/₃.4.³/₂.³/₂.³/₂.4)/₂ -- {3}+60×{4}+24{⁵/₂}

(*1) : Le grand dirhombidodécaèdre disadouci possède 120 arêtes partagées par quatre faces. Si elles sont comptées comme deux paires, alors il existe au total 360 arêtes. À cause de cette dégénérescence des arêtes, il n'est pas toujours considéré comme un polyèdre uniforme.

Renvois

Classes de solides

R = 5 solides de Platon

R+= 4 solides de Kepler-Poinsot

A = 13 solides d'Archimède

C+= 14 polyèdres non convexes avec des faces convexes (tous ces polyèdres uniformes ont les faces qui se coupent les unes les autres)

S+= 39 polyèdres non convexes avec des faces complexes (étoilées)

P = Série infinie des prismes réguliers convexes et des antiprismes

P+= Série infinie des prisme et des antiprismes uniformes non convexes (ceux-ci contiennent tous des faces complexes (étoiles))

T = 11 pavages planaires

Acronyme de Bowers - Un nom unique abrégé prononçable basé sur l'anglais créé par le mathématicien Jonathan Bowers

Indexation uniforme : U01-U80 (d'abord le tétraèdre, les prisme à 76+)

Indexation Kaleido : K01-K80 <K(n)=U(n-5) pour n=6..80> (prismes 1-5, Tétraèdre 6+)

Magnus Wenninger Patrons de polyèdre : W001-W119

1-18 - 5 convexes réguliers et 13 convexes semi-réguliers

20-22, 41 - 4 non convexes réguliers

19-66 48 stellations/composés spéciaux (Non réguliers non données sur cette liste)

67-119 - 53 non convexes uniformes

Chi: la caractéristique d'Euler, $χ$ . Les pavages uniformes sur le plan correspondent à une topologie torique, avec une caractéristique d'Euler égale à zéro.

Pour les pavages du plan, les nombres donnés de sommets, d'arêtes et de faces montrent le ratio de tels éléments dans une période du motif, qui, dans chaque cas, est un losange (quelquefois un losange à angle droit, i.e. un carré).

Note sur les images de figure de sommet :

Les droites blanches de polygone représentent la "figure de sommet" du polygone. Les faces colorées incluses sur les images des figures de sommet aident à voir leurs relations.

Liens externes

Stella: Polyhedron Navigator - Logiciel pour générer et imprimer des patrons pour tous les polyèdres uniformes.

Patrons en papiers

Indexation uniforme : U1-U80, (le tétraèdre en premier)

Les polyèdres uniformes (80), Paul Bourke

http://mathworld.wolfram.com/UniformPolyhedron.html

http://www.mathconsult.ch/showroom/unipoly

Tous les polyèdres uniformes par groupe de rotation

http://gratrix.net/polyhedra/uniform/summary

http://www.it-c.dk/edu/documentation/mathworks/math/math/u/u034.htm

http://www.buddenbooks.com/jb/uniform/

Indexation par Kaleido : K1-K80 (Prisme triangulaire en premier)

http://www.math.technion.ac.il/~rl/kaleido

http://www.math.technion.ac.il/~rl/docs/uniform.pdf Solution uniforme pour les polyèdres uniformes

http://bulatov.org/polyhedra/uniform

http://web.ukonline.co.uk/polyhedra/uniform/uniform.html

Aussi

http://www.polyedergarten.de/polyhedrix/f_klintro.htm

v · d · m

Solides géométriques

Solides de Platon Tétraèdre régulier · Cube · Octaèdre régulier · Icosaèdre régulier · Dodécaèdre régulier

Solides d'Archimède Tétraèdre tronqué · Cube tronqué · Octaèdre tronqué · Dodécaèdre tronqué · Icosaèdre tronqué · Cuboctaèdre · Cube adouci · Icosidodécaèdre · Dodécaèdre adouci · Petit rhombicuboctaèdre · Grand rhombicuboctaèdre · Petit rhombicosidodécaèdre · Grand rhombicosidodécaèdre

Solides de Kepler-Poinsot Petit dodécaèdre étoilé · Grand dodécaèdre étoilé · Grand dodécaèdre · Grand icosaèdre

Solides de Catalan Triakioctaèdre · Tétrakihexaèdre · Triakitétraèdre · Pentakidodécaèdre · Triaki-icosaèdre · Dodécaèdre rhombique · Icositétraèdre pentagonal · Triacontaèdre rhombique · Hexacontaèdre pentagonal · Icositétraèdre trapézoïdal · Hexakioctaèdre · Hexacontaèdre trapézoïdal · Hexaki icosaèdre

Solides de Johnson Gyrobicoupole octogonale allongée · Disphénoïde adouci

Solides de révolution Boule · Cône de révolution · Cylindre de révolution · Tore · Paraboloïde de révolution

Portail de la géométrie

Catégorie :
Polyèdre uniforme

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Liste des polyèdres uniformes de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Liste des polytechniciens célèbres par promotion

Liste des ponts

Regardez d'autres dictionnaires:

Liste Des Polyèdres Uniformes — Les polyèdres uniformes et les pavages forment un groupe bien étudié. Ils sont listés ici pour une comparaison rapide de leurs propriétés et de leurs noms de schéma variés ainsi que de leurs symboles. Cette liste inclut : tous les 75… … Wikipédia en Français

Liste des polyedres uniformes — Liste des polyèdres uniformes Les polyèdres uniformes et les pavages forment un groupe bien étudié. Ils sont listés ici pour une comparaison rapide de leurs propriétés et de leurs noms de schéma variés ainsi que de leurs symboles. Cette liste… … Wikipédia en Français

Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français

Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français

Polyèdre uniforme — Un polyèdre uniforme (en) est un polyèdre qui a pour faces des polygones réguliers et tel qu il existe une isométrie qui applique un sommet quelconque sur un autre. Il en découle que tous les sommets sont congruents, et que le polyèdre… … Wikipédia en Français

Polyedre uniforme — Polyèdre uniforme Un polyèdre uniforme est un polyèdre qui a pour faces des polygones réguliers et peut passer d un sommet à l autre (i.e. il existe une isométrie qui applique un sommet quelconque sur un autre. Il en découle que tous les sommets… … Wikipédia en Français

Symbole de wythoff — Exemple des triangles de construction de Wythoff avec les 7 points générateurs. Les droites des miroirs actifs sont colorés en rouge, jaune et bleu avec les 3 noeuds qui leur sont opposés associés par le symbole de Wythoff. En géométrie, un… … Wikipédia en Français

Symbole de Wythoff — Exemple des triangles de construction de Wythoff avec les 7 points générateurs. Les droites des miroirs actifs sont colorés en rouge, jaune et bleu avec les 3 noeuds qui leur sont opposés associés par le symbole de Wythoff. En géométrie, un… … Wikipédia en Français

Diagramme de Coxeter-Dynkin — Les groupes de Coxeter dans le plan avec les diagrammes équivalents. Les miroirs du domaine sont nommés par les arêtes m1, m2, etc. Les sommets sont colorés par leur ordre de réflexion. Le groupe prismatique [W2xW2] est montré comme un doublement … Wikipédia en Français

Solide d'Archimede — Solide d Archimède En géométrie, un solide d Archimède est un polyèdre convexe semi régulier, fortement symétrique composé de deux sortes (ou davantage) de polygones réguliers se rencontrant à des sommets identiques. Ils sont distincts des… … Wikipédia en Français

18+
© Academic, 2000-2024

Contactez-nous: Support technique, RÉCLAME

Dictionnaires exportation, créé sur PHP,
Joomla,
Drupal,
WordPress, MODx.

Mark and share

Search through all dictionaries

Translate…

Search Internet

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”