Triacontaedre rhombique

Triacontaedre rhombique

Triacontaèdre rhombique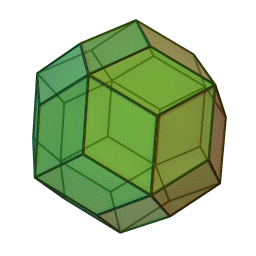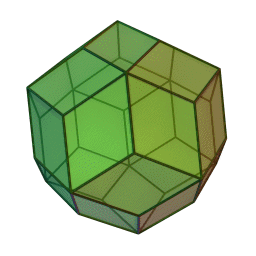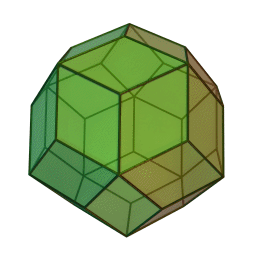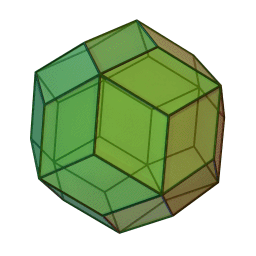

Triacontaèdre rhombique
Triacontaèdre rhombique
Type Solide de Catalan
Faces Losanges
Éléments :
 · Faces
 · Arêtes
 · Sommets
 · Caractéristique		  
30
60
32
2
Faces par sommet 3 et 5
Sommets par face 4
Isométries Icosaédrique
Dual Icosidodécaèdre
Propriétés {{{propriétés}}}

En géométrie, le triacontaèdre rhombique est un polyèdre convexe avec 30 faces en forme de losanges. C'est le dual d'un solide d'Archimède ou solide de Catalan. C'est le dual de l'icosidodécaèdre et un zonoèdre.

Le rapport de la grande diagonale sur la petite diagonale de chaque face est exactement égal au nombre d'or, φ, c’est-à-dire que les angle aigus sur chaque faces mesurent 2 tan-1(1/φ) = tan-1(2), ou approximativement 63,43°. Un losange ainsi obtenu est appelé un losange d'or.

Étant le dual d'un solide d'Archimède, le triacontaèdre rhombique est de faces uniformes, ce qui signifie que le groupe de symétrie du solide agit sur l'ensemble des faces transitivement. En termes élémentaires, ceci signifie que pour deux faces quelconques A et B, il existe une rotation ou une réflexion du solide qui le laisse occuper la même région d'espace lors du déplacement de la face A vers la face B. Le triacontaèdre rhombique est aussi quelque peu spécial en étant un des neuf polyèdres convexes d'arêtes uniformes, les autres étant les cinq solides de Platon, le cuboctaèdre, l'icosidodécaèdre et le dodécaèdre rhombique.

Sommaire

Usages du triacontaèdre rhombique

Le concepteur danois Holger Strøm a utilisé le triacontaèdre rhombique comme une base pour la conception de sa lampe constructible IQ-light™. (IQ pour "Interlocking Quadrilaterals" (quadrilatères interbloquants))

Dans certains jeux de rôle, même s'il y est peu utilisé, et pour l'utilisation en école élémentaire, le triacontaèdre rhombique est utilisé comme dé à trente faces "d30".

Surface et volume

Si son arête est de longueur "a",

  • Son volume vaut :

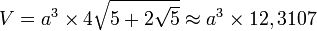
V = a^3 \times 4\sqrt{5+2\sqrt{5}} \approx a^3 \times 12,3107

  • Sa surface vaut :

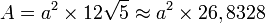
A = a^2 \times 12\sqrt{5} \approx a^2 \times 26,8328

Voir aussi

Références

  • Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979, ISBN 0-486-23729-X

Liens externes


Solides géométriques
Les polyèdres
Les solides de Platon
Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre
Les solides d'Archimède
Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre
Les solides de Kepler-Poinsot
Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre
Les solides de Catalan
Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre
Les solides de Johnson
Les solides de révolution
Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Triaconta%C3%A8dre rhombique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Triacontaedre rhombique de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Triacontaèdre rhombique — Type Solide de Catalan Faces Losanges Éléments :  · Faces  · Arêtes  · Somm …   Wikipédia en Français

  • Triacontaèdre rhombique tronqué — Type Quasi polyèdre de Johnson Faces 12 pentagones 30 hexagones Arêtes 120 (2 types) …   Wikipédia en Français

  • Dodecaedre rhombique — Dodécaèdre rhombique Dodécaèdre rhombique Type Solide de Catalan Faces Losanges Éléments :  · Faces  · Arêtes  · Sommets  · Caractéristique   12 24 14 2 Faces par sommet 3 et 4 …   Wikipédia en Français

  • Dodécaèdre Rhombique — Type Solide de Catalan Faces Losanges Éléments :  · Faces  · Arêtes  · Sommets  · Caractéristique   12 24 14 2 Faces par sommet 3 et 4 …   Wikipédia en Français

  • Dodécaèdre rhombique —  Ne pas confondre avec les autres dodécaèdres. Dodécaèdre rhombique Type …   Wikipédia en Français

  • Dodécaèdre rhombique tronqué — Type Quasi polyèdre de Johnson Faces 6 carrés 12 hexagones Arêtes 48 (2 types) Sommets …   Wikipédia en Français

  • Solide de Catalan — Un dodécaèdre rhombique En mathématiques, un solide de Catalan ou dual archimédien, est un polyèdre dual d un solide d Archimède. Les solides de Catalan ont été nommés ainsi en l honneur du mathématicien belge Eugène Catalan qui fut le premier à… …   Wikipédia en Français

  • Zonoedre — Zonoèdre Un zonoèdre est un polyèdre convexe où chaque face est un polygone avec un centre de symétrie ou, de manière équivalente, une symétrie avec des rotations à 180°. Tout zonoèdre peut être décrit de manière équivalente comme la somme de… …   Wikipédia en Français

  • Zonoèdre — Un zonoèdre est un polyèdre convexe où chaque face est un polygone avec un centre de symétrie ou, de manière équivalente, une symétrie avec des rotations à 180°. Tout zonoèdre peut être décrit de manière équivalente comme la somme de Minkowski d… …   Wikipédia en Français

  • Solide de catalan — Un dodécaèdre rhombique En mathématiques, un solide de Catalan ou dual archimédien, est un polyèdre dual d un solide d Archimède. Les solides de Catalan ont été nommés ainsi en l honneur du mathématicien belge Eugène Catalan qui fut le premier à… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”