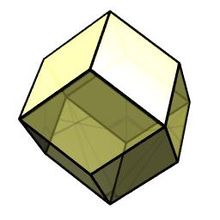
Solide de Catalan
- Solide de Catalan
-
En mathématiques, un solide de Catalan ou dual archimédien, est un polyèdre dual d'un solide d'Archimède. Les solides de Catalan ont été nommés ainsi en l'honneur du mathématicien belge Eugène Catalan qui fut le premier à les décrire en 1865.
Les solides de Catalan sont tous convexes. Ils sont de faces uniformes mais non de sommets uniformes, en raison du fait que les duaux archimédiens sont de sommets uniformes et non de faces uniformes. À la différence des solides de Platon et des solides d'Archimède, les faces des solides de Catalan ne sont pas des polygones réguliers. Par contre, les figures de sommets des solides de Catalan sont régulières, et ont des angles diédraux. De plus, deux des solides de Catalan ont des arêtes uniformes : le dodécaèdre rhombique et le triacontaèdre rhombique. Ceux-ci sont les duaux des deux solides d'Archimède quasi-réguliers.
Comme leurs partenaires duaux archimédiens, il existe deux solides de Catalan chiraux : l'icositétraèdre pentagonal et l'hexacontaèdre pentagonal. Chacun d'eux a deux formes énantiomorphes. Sans compter ces versions énantiomorphes, il existe 13 solides de Catalan au total.
| Nom(s) |
Image |
Dual (solide d'Archimède) |
Faces |
Arêtes |
Sommets |
Polygone de face |
Symétrie |
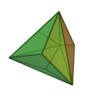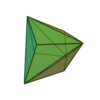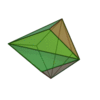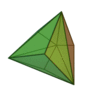
| Triakitétraèdre |
|
Tétraèdre tronqué |
12 |
18 |
8 |
Triangle isocèle
V3,6,6 |
Td |
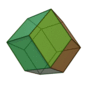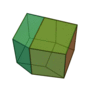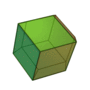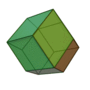
| Dodécaèdre rhombique |
|
Cuboctaèdre |
12 |
24 |
14 |
Losange
V3,4,3,4 |
Oh |
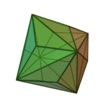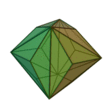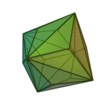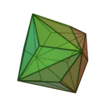
| Triakioctaèdre |
|
Cube tronqué |
24 |
36 |
14 |
Triangle isocèle
V3,8,8 |
Oh |
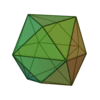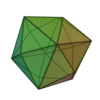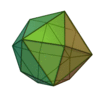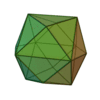
| Tétrakihexaèdre |
|
Octaèdre tronqué |
24 |
36 |
14 |
Triangle isocèle
V4,6,6 |
Oh |
| Icositétraèdre trapézoïdal |
 |
Petit rhombicuboctaèdre |
24 |
48 |
26 |
Trapèze
V3,4,4,4 |
Oh |
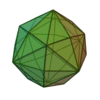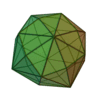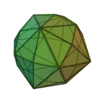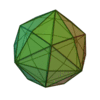
Hexakioctaèdre
|
|
Grand rhombicuboctaèdre |
48 |
72 |
26 |
Triangle scalène
V4,6,8 |
Oh |
Icositétraèdre pentagonal
(deux formes chirales) |
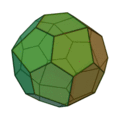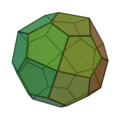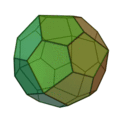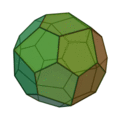
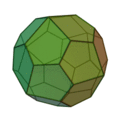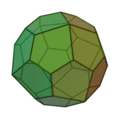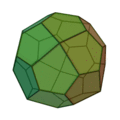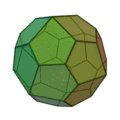 |
Cube adouci |
24 |
60 |
38 |
Pentagone irrégulier
V3,3,3,3,4 |
O |
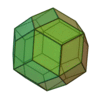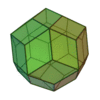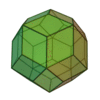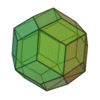
| Triacontaèdre rhombique |
|
Icosidodécaèdre |
30 |
60 |
32 |
Losange
V3,5,3,5 |
Ih |
| Triaki-icosaèdre |
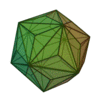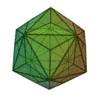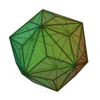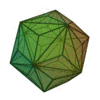
|
Dodécaèdre tronqué |
60 |
90 |
32 |
Triangle isocèle
V3,10,10 |
Ih |
| Pentakidodécaèdre |

|
Icosaèdre tronqué |
60 |
90 |
32 |
Triangle isocèle
V5,6,6 |
Ih |
| Hexacontaèdre trapézoïdal |

|
Petit rhombicosidodécaèdre |
60 |
120 |
62 |
Trapèze
V3,4,5,4 |
Ih |
Hexaki icosaèdre
|

|
Grand rhombicosidodécaèdre |
120 |
180 |
62 |
Triangle scalène
V4,6,10 |
Ih |
Hexacontaèdre pentagonal
(deux formes chirales) |

 |
Dodécaèdre adouci |
60 |
150 |
92 |
Pentagone irrégulier
V3,3,3,3,5 |
I |
Références
- Eugène Catalan Mémoire sur la Théorie des Polyèdres. J. l'École Polytechnique (Paris) 41, 1-71, 1865.
- Alan Holden Shapes, Space, and Symmetry. New York: Dover, 1991.
- Magnus Wenninger Dual Models Cambridge, England: Cambridge University Press, 1983.
- Robert Williams The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc, 1979, (ISBN 0-486-23729-X)
Liens externes
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Solide de Catalan de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Solide de catalan — Un dodécaèdre rhombique En mathématiques, un solide de Catalan ou dual archimédien, est un polyèdre dual d un solide d Archimède. Les solides de Catalan ont été nommés ainsi en l honneur du mathématicien belge Eugène Catalan qui fut le premier à… … Wikipédia en Français
Solide de Johnson — La gyrobicoupole octogonale allongée (J37), un solide de Johnson … Wikipédia en Français
Solide d'Archimede — Solide d Archimède En géométrie, un solide d Archimède est un polyèdre convexe semi régulier, fortement symétrique composé de deux sortes (ou davantage) de polygones réguliers se rencontrant à des sommets identiques. Ils sont distincts des… … Wikipédia en Français
Solide (géométrie) — Solide géométrique En géométrie dans l espace, on définit en général le solide comme l ensemble des points situés à l intérieur d une partie fermée de l espace. On souhaite aussi, naturellement, que la surface délimitant le solide soit d aire… … Wikipédia en Français
Solide de johnson — La gyrobicoupole octogonale allongée (J37), un solide de Johnson … Wikipédia en Français
Solide de platon — En géométrie, un solide de Platon est un polyèdre régulier convexe. Ce sont les analogues tridimensionnels des polygones réguliers convexes. Il y a précisément cinq figures de cette sorte (montrées ci dessous). Elles sont uniques dans le fait que … Wikipédia en Français
Solide geometrique — Solide géométrique En géométrie dans l espace, on définit en général le solide comme l ensemble des points situés à l intérieur d une partie fermée de l espace. On souhaite aussi, naturellement, que la surface délimitant le solide soit d aire… … Wikipédia en Français
Solide platonicien — Solide de Platon En géométrie, un solide de Platon est un polyèdre régulier convexe. Ce sont les analogues tridimensionnels des polygones réguliers convexes. Il y a précisément cinq figures de cette sorte (montrées ci dessous). Elles sont uniques … Wikipédia en Français
Solide de kepler-poinsot — Une face unique est colorée en jaune et entourée de rouge pour aider à identifier les faces. Les solides de Kepler Poinsot sont les polyèdres étoilés réguliers. Chacun possède des faces qui sont des polygones convexes réguliers congruents ou des… … Wikipédia en Français
Solide de revolution — Solide de révolution Un solide de révolution est engendré par une surface plane fermée tournant autour d un axe situé dans la même plan qu elle et ne possédant en commun avec elle aucun point ou seulement des points de sa frontière. Parmi les… … Wikipédia en Français