Polyèdre uniforme

Un polyèdre uniforme (en) est un polyèdre qui a pour faces des polygones réguliers et tel qu'il existe une isométrie qui applique un sommet quelconque sur un autre. Il en découle que tous les sommets sont congruents, et que le polyèdre possède un haut degré de symétrie axiale et rotationnelle.

Les polyèdres uniformes peuvent être réguliers, quasi-réguliers ou semi-réguliers. Les faces n'ont pas besoin d'être convexes, beaucoup de polyèdres uniformes sont aussi des polyèdres étoilés.

En excluant les ensembles infinis, il existe 75 polyèdres uniformes (ou 76 si les arêtes sont autorisées à coïncider).

Les catégories incluent :

L'ensemble infini des prismes uniformes (incluant les prismes étoilés)
L'ensemble infini des antiprismes uniformes (incluant les antiprismes étoilés)
Les 5 solides de Platon - les polyèdres réguliers convexes
Les 4 solides de Kepler-Poinsot - les polyèdres réguliers non-convexes
Les 13 solides d'Archimède - les polyèdres quasi-réguliers convexes et les polyèdres semi-réguliers
Les 14 polyèdres non-convexes à faces convexes
Les 39 polyèdres non-convexes à faces non-convexes
1 polyèdre trouvé par John Skilling (en) avec les paires d'arêtes qui coïncident.

Ils peuvent aussi être groupés par leur groupe de symétrie, ce qui est fait ci-dessous.

Sommaire

1 Histoire
- 1.1 Indexation
2 Formes convexes et arrangements de sommet fondamentaux
- 2.1 Définition des opérations
3 Formes non-convexes listées par groupes de symétrie et par arrangements de sommet
4 Voir aussi
5 Liens externes

Histoire

Les solides de Platon sont connus depuis l'Antiquité par les Grecs classiques et ont été étudiés par Platon, Théétète et Euclide.
Johannes Kepler (1571-1630) fut le premier à publier la liste complète des solides d'Archimède après la perte du travail original d'Archimède.
Kepler (1619) a découvert deux des solides de Kepler-Poinsot réguliers et Louis Poinsot (1809) a découvert les deux autres.
Des 66 qui restaient, 37 furent découverts par Albert Badoureau (1881). Edmund Hess (en) (1878) en découvrit 2 de plus et Pitsch (1881) en découvrit 18 indépendamment, dont 15 nouveaux.
Le célèbre géomètre Coxeter découvrit les 12 restants en collaboration avec J. C. P. Miller (en) (1930-1932) mais ne le publia pas. M.S. (en) et H.C. Longuet-Higgins ont indépendamment découvert 11 d'entre eux.
En 1954, Coxeter, M.S. Longuet-Higgins et Miller publièrent la liste des polyèdres uniformes.
En 1970 S. P. Sopov démontra leur conjecture établissant que la liste était complète.
En 1974, Magnus Wenninger (en) publia son livre, Polyhedron models (en) (patrons de polyèdres), qui est la première liste entière publiée des 75 polyèdres uniformes non prismatiques, dont beaucoup, auparavant sans nom publié, avaient été baptisés par Norman Johnson.
En 1975, John Skilling prouva indépendamment la complétude de cette liste, et montra que si la définition du polyèdre uniforme est assouplie pour autoriser la coïncidence des arêtes alors seule une possibilité supplémentaire est offerte.
En 1993, Zvi Har'El produisit une construction informatique complète des polyèdres uniformes et de leurs duaux via leurs construction kaleïdoscopiques via un programme informatique appelé Kaleido, et résumé dans un article intitulé Uniform Solution for Uniform Polyhedra., comptant les solides 1-80.
En 1993 aussi, R. Mäder porta cette solution Kaleido vers Mathematica avec un système d'indexation légèrement différent.

Indexation

Il existe quatre efforts d'indexation majeurs publiés à partir des travaux ci-dessus. Pour les distinguer, ils sont donnés par différentes lettres d'indexation, C pour la première énumération des solides par Coxeter en 1954, W pour le livre de 1974 sur les patrons de polyèdres par Wenninger, K pour la solution Kaleido de 1993, et U pour la solution de Maeder utilisée par Mathematica et reproduite extensivement ailleurs.

[C] 1954 : cet article listait les polyèdres uniformes par solides de 15 à 92. En démarrant avec 15-32 pour les formes convexes, 33-35 pour les 3 ensembles prismatiques infinis et finissant avec 36-92 pour les formes non-convexes.
[W] 1974 : le livre de Wenninger Polyhedron model énumérait les solides de 1 à 119 : 1-5 pour les solides de Platon, 6-18 pour les solides d'Archimède, 19-66 pour les formes étoilées incluant les 4 polyèdres réguliers non-convexes et finissait avec 67-119 pour les polyèdres uniformes non-convexes.
[K] 1993 Kaleido : les 80 solides donnés dans la solution Kaleido étaient groupés par symétrie, énumérés de 1 à 80 : 1-5 comme représentatifs des familles infinies des formes prismatiques avec la symétrie diédrale, 6-9 avec la symétrie tétraédrique (en), 10-26 avec la symétrie octaédrique (en), 46-80 avec la symétrie icosaédrique (en).
[U] 1993 Mathematica : ce listing suivit celui de Kaleido, mais déplaça les 5 formes prismatiques vers la fin, décalant les formes non-prismatiques de 5, de 1 à 75.

Formes convexes et arrangements de sommet fondamentaux

Les polyèdres uniformes convexes peuvent être nommés par les opérations de construction de Wythoff sur une forme parent.

Note : les dièdres font partie d'un ensemble infini de polyèdres à deux côtés (2 polygones identiques) qui engendre les prismes comme formes tronquées.

Chacune de ces formes convexes définit un ensemble de sommets qui peut être identifié pour les formes non-convexes dans la prochaine section.

	Parent	Tronqué	Rectifié	Bitronqué (dual tronqué)	Birectifié (dual)	Biseauté	Omnitronqué (Biseauté-tronqué)	Adouci
Symbole de Schläfli Étendu	$\begin{Bmatrix} p , q \end{Bmatrix}$	$t\begin{Bmatrix} p , q \end{Bmatrix}$	$\begin{Bmatrix} p \\ q \end{Bmatrix}$	$t\begin{Bmatrix} q , p \end{Bmatrix}$	$\begin{Bmatrix} q , p \end{Bmatrix}$	$r\begin{Bmatrix} p \\ q \end{Bmatrix}$	$t\begin{Bmatrix} p \\ q \end{Bmatrix}$	$s\begin{Bmatrix} p \\ q \end{Bmatrix}$
Symbole de Schläfli Étendu	t₀{p,q}	t_0,1{p,q}	t₁{p,q}	t_1,2{p,q}	t₂{p,q}	t_0,2{p,q}	t_0,1,2{p,q}	s{p,q}
Symbole de Wythoff p-q-2	q \| p 2	2 q \| p	2 \| p q	2 p \| q	p \| q 2	p q \| 2	p q 2 \|	\| p q 2
Diagramme de Coxeter-Dynkin (variations)

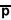
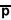
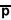
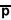
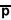
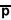
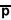
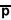
	(o)-p-o-q-o	(o)-p-(o)-q-o	o-p-(o)-q-o	o-p-(o)-q-(o)	o-p-o-q-(o)	(o)-p-o-q-(o)	(o)-p-(o)-q-(o)	( )-p-( )-q-( )
	xPoQo	xPxQo	oPxQo	oPxQx	oPoQx	xPoQx	xPxQx	sPsQs
	[p,q]:001	[p,q]:011	[p,q]:010	[p,q]:110	[p,q]:100	[p,q]:101	[p,q]:111	[p,q]:111s
Figure de sommet	p^q	(q.2p.2p)	(p.q.p.q)	(p.2q.2q)	q^p	(p.4.q.4)	(4.2p.2q)	(3.3.p.3.q)
Tétraédrique 3-3-2	{3,3}	(3.6.6)	(3.3.3.3)	(3.6.6)	{3,3}	(3.4.3.4)	(4.6.6)	(3.3.3.3.3)
Octaédrique 4-3-2	{4,3}	(3.8.8)	(3.4.3.4)	(4.6.6)	{3,4}	(3.4.4.4)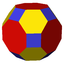	(4.6.8)	(3.3.3.3.4)
Icosaédrique 5-3-2	{5,3}	(3.10.10)	(3.5.3.5)	(5.6.6)	{3,5}	(3.4.5.4)	(4.6.10)	(3.3.3.3.5)
Diédrique p-2-2 Exemple p=5	{5,2}	2.10.10	2.5.2.5	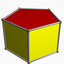4.4.5	{2,5}	2.4.5.4	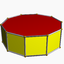4.4.10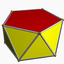	3.3.3.5

Définition des opérations

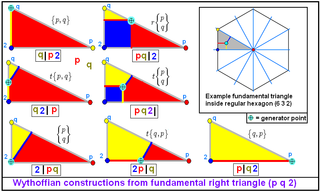
Opération	Étendu Symboles de Schläfli		Description
Parent	t₀{p,q}	$\begin{Bmatrix} p , q \end{Bmatrix}$	Polyèdre régulier quelconque ou pavage
Rectifié	t₁{p,q}	$\begin{Bmatrix} p \\ q \end{Bmatrix}$	Les arêtes sont pleinement tronquées en points uniques. Le polyèdre maintenant possède les faces combinées du parent et du dual.
Birectifié Dual	t₂{p,q}	$\begin{Bmatrix} q , p \end{Bmatrix}$	Le birectifié (dual) est une troncature plus poussée c’est-à-dire que les faces originales sont réduites à des points. Les nouvelles faces sont formées sous chaque sommet du parent. Le nombre d'arêtes est inchangé et est tourné à 90 degrés. Le dual d'un polyèdre régulier {p, q} est aussi un polyèdre régulier {q, p}.
Tronqué	t_0,1{p,q}	$t\begin{Bmatrix} p , q \end{Bmatrix}$	Chaque sommet original est découpé, avec de nouvelles faces remplissant le trou. La troncature possède un degré de liberté, qui a une solution qui créée un polyèdre uniforme tronqué. Le polyèdre a ses faces originales doublées par côtés, et contient les faces du dual.
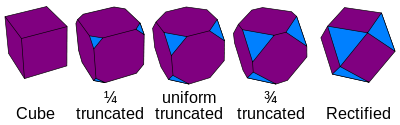
Bitronqué	t_1,2{p,q}	$t\begin{Bmatrix} q , p \end{Bmatrix}$	Identique au dual tronqué.
Biseauté (ou rhombé) (développé)	t_0,2{p,q}	$r\begin{Bmatrix} p \\ q \end{Bmatrix}$	En ajout à la troncature des sommets, chaque arête originale est rabotée faisant apparaître à la place de nouvelles faces rectangulaires. Un biseautage uniforme est à mi-chemin entre le parent et les formes duales.
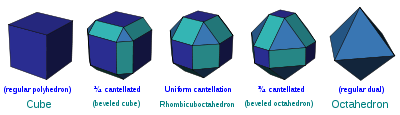
Omnitroncature (ou biseautage-troncature) (ou rhombi-tronqué)	t_0,1,2{p,q}	$t\begin{Bmatrix} p \\ q \end{Bmatrix}$	Les opérations de troncature et de biseautage sont appliquées ensemble, créant une forme omnitronquée qui a les faces du parent doublées sur les côtés, les faces du dual doublées sur les côtés et des carrés où les arêtes originales existaient.
Adouci	s{p,q}	$s\begin{Bmatrix} p \\ q \end{Bmatrix}$	L'adoucissement prend la forme omnitronquée et rectifie les sommets alternativement (cette opération est seulement possible pour les polyèdres avec toutes les faces sur les côtés paires). Toutes les faces originales finissent avec la moitié des côtés, et le carré dégénère en arêtes. Puisque les formes omnitronquées ont 3 faces/sommet, de nouveaux triangles sont formés.

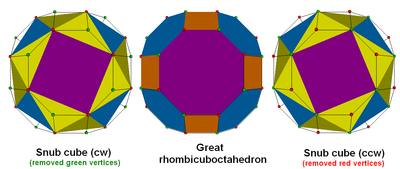
Formes non-convexes listées par groupes de symétrie et par arrangements de sommet

Tous les polyèdres uniformes sont listés ci-dessous par leurs groupes de symétrie et sous-groupés par leurs arrangements de sommet.

Les polyèdres réguliers sont marqués par leurs symboles de Schläfli. Les autres polyèdres non-réguliers uniformes sont listés par leur configuration de sommet ou par l'index des polyèdre uniforme U(1-80).

Note : Pour les formes non-convexes, un descripteur supplémentaire Non-uniforme est utilisé lorsque l'enveloppe convexe de l'arrangement de sommet possède la même topologie que l'un d'entre-eux, mais possède des faces non-régulières. Par exemple, une forme biseautée non-uniforme peut avoir des rectangles créés à la place d'arêtes plutôt que des carrés.

Symétrie tétraédrique

Il existe deux polyèdres uniformes convexes, le tétraèdre et le tétraèdre tronqué, et une forme non-convexe, le tétrahémihexaèdre qui possède une symétrie tétraédrique. Le tétraèdre est un polyèdre autodual.

En plus, l'octaèdre, l'octaèdre tronqué, le cuboctaèdre et l'icosaèdre ont une symétrie tétraédrique de même qu'une symétrie plus élevée. Ils sont ajoutés pour l'exhaustivité ci-dessous, bien que leurs formes non-convexes avec la symétrie octaédrique ne soient pas incluses ici.

Groupe de sommet	Convexe	Non-convexe
(Tétraèdre)	{3,3}
Tronqué (*)	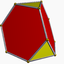(3.6.6)
Rectifié (*)	64px {3,4}	(4.3/2.4.3)
Biseauté (*)	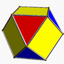(3.4.3.4)
Omnitronqué (*)	64px (4.6.6)
Adouci (*)	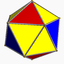{3,5}

Symétrie octaédrique

Il existe 8 formes convexes et 10 formes non-convexes avec la symétrie octaédrique.

Groupe de sommet	Convexe	Non-convexe
(Octaédrique)	{3,4}
Tronqué (*)	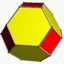(4.6.6)
Rectifié (*)	(3.4.3.4)	(6.4/3.6.4)	(6.3/2.6.3)
Dual tronqué (*)	(3.8.8)	(4.8/3.4/3.8/5)	(8/3.3.8/3.4)	(4.3/2.4.4)
Dual (*)	{4,3}
Biseauté (*)	(3.4.4.4)	(4.8.4/3.8)	(8.3/2.8.4)	(8/3.8/3.3)
Omnitronqué (*)	(4.6.8)
Omnitronqué non-uniforme (*)	(4.6.8)	(8/3.4.6)	(8/3.6.8)
Adouci (*)	(3.3.3.3.4)

Symétrie icosaédrique

Il existe 8 formes convexes et 46 formes non-convexes avec la symétrie icosaédrique (ou 47 formes non-convexes si le polyèdre de Skilling est inclus). Certaines formes adoucies non-convexes ont une symétrie chirale non-uniforme, et certaines ont une symétrie achirale.

Il existe beaucoup de formes non-uniformes de degrés variés de troncature et de biseautage.

Groupe de sommet	Convexe	Non-convexe
(Icosaédrique)	{3,5}	{5/2,5}	{5,5/2}	{3,5/2}
Tronqué (*)	(5.6.6)
Tronqué non-uniforme (*)	(5.6.6)	U32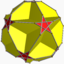	U37	U61	U38	U44	U56	U67	U73
Rectifié (*)	(3.5.3.5)	U49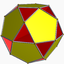	U51	U54	U70	U71	U36	U62	U65
Dual tronqué (*)	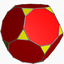(3.10.10)	U42	U48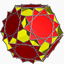	U63
Dual tronqué non-uniforme (*)	(3.10.10)	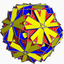U68	U72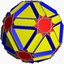	U45
Dual (*)	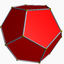{5,3}	{5/2,3}	U30	U41	U47
Biseauté (*)	(3.4.5.4)	U33	U39
Biseauté non-uniforme (*)	(3.4.5.4)	U31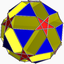	U43	U50	U55	U58	U75	U64	U66
Omnitronqué (*)	(4.6.10)
Omnitronqué non-uniforme (*)	(4.6.10)	U59
Adouci (*)	(3.3.3.3.5)
Adouci non-uniforme (*)	(3.3.3.3.5)	U40	U46	U57	U69	U60	U74

Polyèdre de Skilling

Un polyèdre non-convexe supplémentaire s'appelle le Grand dirhombidodécaèdre disadouci, aussi connu sous le nom polyèdre de Skilling, qui est de sommet uniforme, mais dont les paires d'arêtes coïncident dans l'espace telles que quatre faces se rencontrent à certains sommets. Il est quelquefois, mais pas toujours, compté comme un polyèdre uniforme. Il possède une symétrie I_h.

Symétrie diédrique

Il existe deux ensembles infinis de polyèdres uniformes avec la symétrie diédrique :

Les prismes, pour chaque nombre rationnel p/q > 2, avec le groupe de symétrie D_ph;
Les antiprismes, pour chaque nombre rationnel p/q > 3/2, avec le groupe de symétrie D_pd si q est impair, D_ph si q est pair.

Si p/q est un nombre entier, i.e. si q = 1, le prisme ou l'antiprisme est convexe (la fraction est toujours supposée irréductible).

La différence entre les groupes de symétrie prismatiques et antiprismatique réside dans le fait que D_ph possède un plan de réflexion parallèle au polygone {p/q}, alors que D_pd n'en possède pas.

Un antiprisme avec p/q < 2 est croisé; sa figure de sommet ressemble à un nœud papillon. Si p/q ≤ 3/2, aucun antiprisme ne peut exister, comme sa figure de sommet violerait l'inégalité triangulaire.

Note : le cube et l'octaèdre sont listés ici avec la symétrie diédrique (en tant que prisme tétragonal et antiprisme trigonal respectivement), bien qu'étant uniformément coloré, ils ont aussi une symétrie octaédrique.

Groupe de symétrie	Convexe	Non-convexe
d_3h	3.3.4
d_3d	3.3.3.3
d_4h	64px 4.4.4
d_4d	3.3.3.4
d_5h	4.4.5	4.4.5/2	3.3.3.5/2
d_5d	3.3.3.5	3.3.3.5/3
d_6h	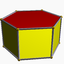4.4.6
d_6d	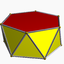3.3.3.6
d_7h	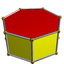4.4.7	4.4.7/2	4.4.7/3	3.3.3.7/2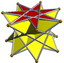	3.3.3.7/4
d_7d	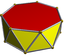3.3.3.7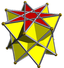	3.3.3.7/3
d_8h	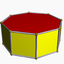4.4.8	64px 4.4.4.8/3
d_8d	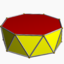3.3.3.8	3.3.3.8/3 3.3.3.8/5
d_9h	64px 4.4.9	4.4.9/2	3.3.3.9/2	3.3.3.9/4
d_9d	3.3.3.9	3.3.3.9/5
d_10h	4.4.10	4.4.10/3
d_10d	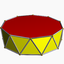3.3.3.10	3.3.3.10/3
d_11h	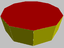4.4.11	4.4.11/2 4.4.11/3 4.4.11/4 4.4.11/5	3.3.3.11/2 3.3.3.11/4 3.3.3.11/6
d_11d	3.3.3.11	3.3.3.11/3 3.3.3.11/5 3.3.3.11/7
d_12h	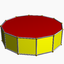4.4.12	4.4.12/5	3.3.3.12/7
d_12d	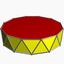3.3.3.12	3.3.3.12/5
...

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Uniform polyhedron » (voir la liste des auteurs)
Brückner, M. Vielecke und vielflache. Theorie und geschichte.. Leipzig, Germany: Teubner, 1900. [1]
H.S.M. Coxeter, M.S. Longuet-Higgins, J.C.P. Miller, Uniform polyhedra, Phil. Trans. 1954, 246 A, 401-50 [2]
S. P. Sopov A proof of the completeness on the list of elementary homogeneous polyhedra. (Russian) Ukrain. Geometr. Sb. No. 8, (1970), 139-156
John Skilling (en), The complete set of uniform polyhedra., Philos. Trans. Roy. Soc. London Ser. A 278 (1975), 111-135 [3]
Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57-110, 1993. Zvi Har’El [4], Kaleido software, Images, dual images
Mäder, R. E. Uniform Polyhedra. Mathematica J. 3, 48-57, 1993. [5]

Voir aussi

Liens externes

(en) Stella: Polyhedron Navigator - Logiciel pour générer et imprimer les patrons de tous les polyèdres uniformes
(en) Patrons en papier
(en) Solution uniforme pour polyèdre uniforme
(en) Les polyèdres uniformes
(en) Virtual Polyhedra Les polyèdres uniformes
(en) Eric W. Weisstein. "Uniform Polyhedron." À partir de MathWorld--A Wolfram Web Resource.
(de) Patrons en papier des polyèdres uniformes (et les autres)

v · liste détaillée)^a
Réguliers convexes 5 solides de Platon	tétraèdre • cube • octaèdre • dodécaèdre • icosaèdre
Réguliers étoilés 4 solides de Kepler-Poinsot	petit dodécaèdre étoilé • grand dodécaèdre étoilé • grand dodécaèdre • grand icosaèdre
Quasi-réguliers convexes 2 solides d'Archimède	cuboctaèdre • icosidodécaèdre
Quasi-réguliers étoilés 5 non nommés	dodécadodécaèdre • grand icosidodécaèdre • petit icosidodécaèdre ditrigonal • dodécadodécaèdre ditrigonal • grand icosidodécaèdre ditrigonal
Semi-réguliers convexes non prismatiques 11 solides d'Archimède	tétraèdre tronqué • cube tronqué • octaèdre tronqué • dodécaèdre tronqué • icosaèdre tronqué • cube adouci • dodécaèdre adouci • petit rhombicuboctaèdre • grand rhombicuboctaèdre • petit rhombicosidodécaèdre • grand rhombicosidodécaèdre
Semi-réguliers convexes prismatiques infinité	antiprisme carré • prisme pentagonal • antiprisme pentagonal • prisme hexagonal • antiprisme hexagonal • prisme heptagonal • antiprisme heptagonal • prisme octogonal • antiprisme octogonal • …
Semi-réguliers étoilés non prismatiques à faces convexes 13 non nommès^b	tétrahémihexaèdre • cubohémioctaèdre • octahémioctaèdre • petit rhombihexaèdre • petit cubicuboctaèdre • grand rhombicuboctaèdre uniforme • petit dodécahémidodécaèdre • petit icosihémidodécaèdre • petit dodécicosaèdre • petit rhombidodécaèdre • petit dodécicosidodécaèdre • rhombicosaèdre • grand icosicosidodécaèdre
Semi-réguliers étoilés non prismatiques à faces étoilées 35 non nommés^b	hexaèdre tronqué étoilé • grand rhombihexaèdre • grand cubicuboctaèdre • grand dodécahémidodécaèdre • petit dodécahémicosaèdre • grand dodécahémicosaèdre • grand icosihémidodécaèdre • cuboctaèdre cubitronqué • grand cuboctaèdre tronqué • grand dodécaèdre tronqué • petit dodécaèdre étoilé tronqué • grand dodécaèdre étoilé tronqué • grand icosaèdre tronqué • grand dodécicosaèdre • grand rhombidodécaèdre • icosidodécadodécaèdre • petit dodécicosidodécaèdre ditrigonal • grand dodécicosidodécaèdre ditrigonal • grand dodécicosidodécaèdre • petit icosicosidodécaèdre • rhombidodécadodécaèdre • grand rhombicosidodécaèdre uniforme • dodécadodécaèdre adouci • dodécadodécaèdre adouci inversé • grand icosidodécaèdre adouci • grand icosidodécaèdre adouci inversé • grand icosidodécaèdre rétroadouci • grand dodécicosidodécaèdre adouci • icosidodécadodécaèdre adouci • petit icosicosidodécaèdre adouci • petit icosicosidodécaèdre rétroadouci • grand dirhombicosidodécaèdre • dodécadodécaèdre icositronqué • dodécadodécaèdre tronqué • grand icosidodécaèdre tronqué
Semi-réguliers étoilés prismatiques infinité	prisme pentagrammique • antiprisme pentagrammique • prisme heptagrammique (7/3) • prisme heptagrammique (7/2) • antiprisme pentagrammique croisé • antiprisme heptagrammique (7/2) • antiprisme heptagrammique (7/4) • antiprisme heptagrammique (7/2) croisé • antiprisme heptagrammique (7/4) croisé • …
Polyèdre de Skilling^c	grand dirhombidodécaèdre disadouci
Autres classes de polyèdres notables : solides de Catalan • bipyramides • trapèzoèdres • solides de Johnson Notes : ^aListe de H.S.M. Coxeter plus le solide de Skilling. Selon l'acceptation ou non de polyèdres particuliers (à faces passant par le centre, à arêtes dégénérées, à faces dont les deux côtés sont visibles, etc.), le nombre de polyèdres étoilés uniformes non réguliers (hors séries prismatiques) peut varier de 20 à 94 (54 dans la présente liste). ^bInclut les polyèdres dont les faces passent par le centre (leur nom comprend l'affixe « hémi »).^cParfois exclu des polyèdres uniformes car certaines de ses arêtes coïncident.

Portail de la géométrie

Catégorie :

Polyèdre uniforme

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Polyèdre uniforme de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Polyedre uniforme — Polyèdre uniforme Un polyèdre uniforme est un polyèdre qui a pour faces des polygones réguliers et peut passer d un sommet à l autre (i.e. il existe une isométrie qui applique un sommet quelconque sur un autre. Il en découle que tous les sommets… … Wikipédia en Français
Polyedre etoile non-convexe — Polyèdre étoilé non convexe Un prisme pentagrammique, avec une figure de sommet 4.4.5/2 En géométrie, un polyèdre uniforme non convexe, ou polyèdre étoilé uniforme, est un polyèdre uniforme auto coupant. Il peut contenir soit des faces… … Wikipédia en Français
Polyèdre étoilé non-convexe — Un prisme pentagrammique, avec une figure de sommet 4.4.5/2 En géométrie, un polyèdre uniforme non convexe, ou polyèdre étoilé uniforme, est un polyèdre uniforme auto coupant. Il peut contenir soit des faces polygonales non convexes, des figures… … Wikipédia en Français
Polyedre etoile — Polyèdre étoilé En géométrie, le terme polyèdre étoilé ne semble pas avoir été défini proprement, même si l objet est pensé dans le sens commun. Nous pouvons dire qu un polyèdre étoilé est un polyèdre qui possède une certaine qualité répétitive… … Wikipédia en Français
Polyèdre étoilé non convexe — Un prisme pentagrammique, avec une figure de sommet 4.4.5/2 En géométrie, un polyèdre uniforme non convexe, ou polyèdre étoilé uniforme, est un polyèdre uniforme auto coupant. Il peut contenir soit des faces polygonales non convexes, des figures… … Wikipédia en Français
Polyèdre étoilé — En géométrie, le terme polyèdre étoilé ne semble pas avoir été défini proprement, même si l objet est pensé dans le sens commun. Nous pouvons dire qu un polyèdre étoilé est un polyèdre qui possède une certaine qualité répétitive de non convexité… … Wikipédia en Français
Polyedre — Polyèdre Un polyèdre particulier en dimension 3 : le dodécaèdre Un polyèdre est une forme géométrique à trois dimensions ayant des faces planes qui se rencontrent le long d arêtes droites. Le mot polyèdre provient du grec classique πολυεδρον … Wikipédia en Français
Polyedre semi-regulier — Polyèdre semi régulier Un polyèdre semi régulier est un polyèdre avec des faces régulières et un groupe de symétrie qui est transitif sur ses sommets. Ou au moins, c est ce qui découle de la définition de 1900 de Gossett sur le polytope semi… … Wikipédia en Français
Polyèdre semi régulier — Un polyèdre semi régulier est un polyèdre avec des faces régulières et un groupe de symétrie qui est transitif sur ses sommets. Ou au moins, c est ce qui découle de la définition de 1900 de Gossett sur le polytope semi régulier le plus… … Wikipédia en Français
Polyedre oblique infini — Polyèdre oblique infini En géométrie, les polyèdres obliques infinis sont une définition étendue des polyèdres, créés par des faces polygonales régulières, et des figures de sommet non planaires. Beaucoup sont directement reliés aux nids d… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Polyèdre uniforme

Sommaire

Histoire

Indexation

Formes convexes et arrangements de sommet fondamentaux

Définition des opérations

Formes non-convexes listées par groupes de symétrie et par arrangements de sommet

Symétrie tétraédrique

Symétrie octaédrique

Symétrie icosaédrique

Polyèdre de Skilling

Symétrie diédrique

Références

Voir aussi

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Polyèdre uniforme

Sommaire

Histoire

Indexation

Formes convexes et arrangements de sommet fondamentaux

Définition des opérations

Formes non-convexes listées par groupes de symétrie et par arrangements de sommet

Symétrie tétraédrique

Symétrie octaédrique

Symétrie icosaédrique

Polyèdre de Skilling

Symétrie diédrique

Références

Voir aussi

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link