- Hexacontaedre trapezoidal
-
Hexacontaèdre trapézoïdal
Hexacontaèdre trapézoïdal 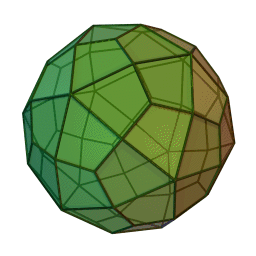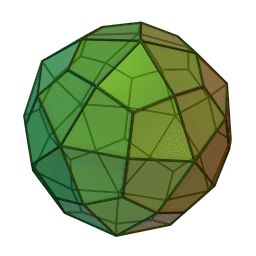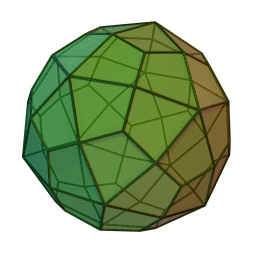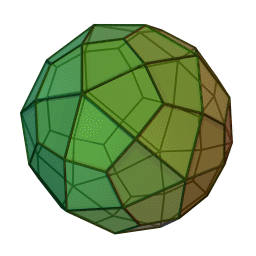
Type Solide de Catalan Faces Cerfs-volants Éléments :
· Faces
· Arêtes
· Sommets
· Caractéristique
60
120
62
2Faces par sommet 3, 4 et 5 Sommets par face 4 Isométries Icosaédrique Dual Petit rhombicuboctaèdre Propriétés Convexe, uniformité des faces Un hexacontaèdre trapézoïdal est un solide de Catalan qui ressemble un peu à un dodécaèdre enflé. Il est quelquefois appelé un hexacontaèdre deltoïdal ou hexacontaèdre strombique. Il est composé de 60 faces en forme de cerfs-volants. Son dual est le petit rhombicuboctaèdre, c'est le seul dual d'un solide d'Archimède qui n'a pas de cycle hamiltonien à travers ses sommets.
Voir aussi
- Deltoèdre
Références
- Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications, 1979, ISBN 0-486-23729-X
Liens externes
Solides géométriques Les polyèdres Les solides de Platon Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre Les solides d'Archimède Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre Les solides de Kepler-Poinsot Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre Les solides de Catalan Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre Les solides de Johnson Les solides de révolution Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution - Portail de la géométrie
Catégorie : Polyèdre
Wikimedia Foundation. 2010.
