Liste Des Polyèdres Uniformes

Liste Des Polyèdres Uniformes

Liste des polyèdres uniformes

Les polyèdres uniformes et les pavages forment un groupe bien étudié. Ils sont listés ici pour une comparaison rapide de leurs propriétés et de leurs noms de schéma variés ainsi que de leurs symboles.

Cette liste inclut :

Ce qui n'est pas inclus :

  • 40 polyèdres uniformes potentiels avec des figures de sommet dégénérées qui ont des arêtes qui se chevauchent (non comptés par Coxeter);
  • 14 pavages uniformes avec des faces non-convexes;
  • l'ensemble infini des pavages hyperboliques uniformes.

Sommaire

Table des polyèdres

Les formes convexes sont listées en ordre de degrés de configuration de sommet à partir de 3 faces/sommet et au-dessus, et en augmentant les cotés par face. Cet ordre permet de montrer des similarités topologiques.

Formes convexes (3 faces/sommet)

Nom Image Classe de
solide		 Symbole de
Wythoff		 Figure de sommet Acronyme
de Bowers		 Groupe de
symétrie		 W# U# K# Sommets Arêtes Faces Chi Faces par type
Tétraèdre Tetrahedron.png R 3|2 3 Tetrahedron vertfig.png
3.3.3		 Tet Td W001 U01 K06 4 6 4 2 4{3}
Prisme triangulaire Triangular prism.png P 2 3|2 Fichier:Triangular prism vertfig.svg
3.4.4		 Trip D3h -- -- -- 6 9 5 2 2{3}+3{4}
Tétraèdre tronqué 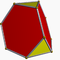Truncated tetrahedron.png A 2 3|3 Truncated tetrahedron vertfig.png
3.6.6		 Tut Td W006 U02 K07 12 18 8 2 4{3}+4{6}
Cube tronqué Truncated hexahedron.png A 2 3|4 Truncated cube vertfig.png
3.8.8		 Tic Oh W008 U09 K14 24 36 14 2 8{3}+6{8}
Dodécaèdre tronqué 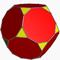Truncated dodecahedron.png A 2 3|5 Truncated dodecahedron vertfig.png
3.10.10		 Tid Ih W010 U26 K31 60 90 32 2 20{3}+12{10}
Pavage hexagonal tronqué Uniform tiling 63-t01.png T 2 3|6 Truncated hexagonal tiling vertfig.png
3.12.12		 Toxat P6m -- -- -- 6n 9n 3n 0 n{12}+2n{3}
Pavage heptagonal tronqué T 2 3|7 3.14.14 -- *732 -- -- -- 0
Cube Hexahedron.png R 3|2 4 Cube vertfig.png
4.4.4		 Cube Oh W003 U06 K11 8 12 6 2 6{4}
Prisme pentagonal Pentagonal prism.png P 2 5|2 Pentagonal prism vertfig.png
4.4.5		 Pip D5h -- U76 K01 10 15 7 2 5{4}+2{5}
Prisme hexagonal 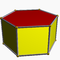Hexagonal prism.png P 2 6|2 Hexagonal prism vertfig.png
4.4.6		 Hip D6h -- -- -- 12 18 8 2 6{4}+2{6}
Prisme octogonal 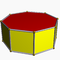Octagonal prism.png P 2 8|2 Octagonal prism vertfig.png
4.4.8		 Op D8h -- -- -- 16 24 10 2 8{4}+2{8}
Prisme décagonal 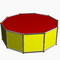Decagonal prism.png P 2 10|2 Decagonal prism vf.png
4.4.10		 Dip D10h -- -- -- 20 30 12 2 10{4}+2{10}
Prisme dodécagonal 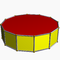Dodecagonal prism.png P 2 12|2 Fichier:Dodecagonal prism vf.png
4.4.12		 Twip D12h -- -- -- 24 36 14 2 12{4}+2{12}
Octaèdre tronqué 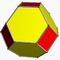Truncated octahedron.png A 2 4|3 Truncated octahedron vertfig.png
4.6.6		 Toe Oh W007 U08 K13 24 36 14 2 6{4}+8{6}
Grand rhombicuboctaèdre Great rhombicuboctahedron.png A 2 3 4| Great rhombicuboctahedron vertfig.png
4.6.8		 Girco Oh W015 U11 K16 48 72 26 2 12{4}+8{6}+6{8}
Grand rhombicosidodécaèdre Great rhombicosidodecahedron.png A 2 3 5| Great rhombicosidodecahedron vertfig.png
4.6.10		 Grid Ih W016 U28 K33 120 180 62 2 30{4}+20{6}+12{10}
Pavage grand rhombitrihexagonal Uniform tiling 63-t012.png T 2 3 6| Great rhombitrihexagonal tiling vertfig.png
4.6.12		 Othat p6m -- -- -- 12n 18n 6n 0 3n{4}+2n{6}+n{12}
Pavage grand rhombitriheptagonal Uniform tiling 73-t012.png T 2 3 7| 4.6.14 -- *732 -- -- -- 14n 21n 7n 0 3n{4}+2n{7}+n{14}
Pavage carré tronqué Uniform tiling 44-t01.png T 2 4|4 Truncated square tiling vertfig.png
4.8.8		 Tosquat p4m -- -- -- 4n 6n 2n 0 n{4}+n{8}
Dodécaèdre 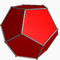Dodecahedron.png R 3|2 5 Dodecahedron vertfig.png
5.5.5		 Doe Ih W005 U23 K28 20 30 12 2 12{5}
Icosaèdre tronqué Truncated icosahedron.png A 2 5|3 Truncated icosahedron vertfig.png
5.6.6		 Ti Ih W009 U25 K30 60 90 32 2 12{5}+20{6}
Pavage triangulaire tronqué d'ordre 7 T 2 7|3 7.6.6 -- *732 -- -- -- 0
Pavage hexagonal Uniform tiling 63-t0.png T 3|2 6 Hexagonal tiling vertfig.png
6.6.6		 Hexat p6m -- -- -- 2n 3n n 0 n{6}
Pavage heptagonal d'ordre 3 Uniform tiling 73-t0.png T 3|2 7 7.7.7 - *732 -- -- -- 2n 3n n 0 n{7}

Formes convexes (4 faces/sommet)

Nom Image Classe de
solide		 Symbole de
Wythoff		 Figure de sommet Acronyme
de Bowers		 Groupe de
symétrie		 W# U# K# Sommets Arêtes Faces Chi Faces par type
Octaèdre Octahedron.png R 4|2 3 Octahedron vertfig.png
3.3.3.3		 Oct Oh W002 U05 K10 6 12 8 2 8{3}
Antiprisme carré Square antiprism.png P |2 2 4 Square antiprism vertfig.png
3.3.3.4		 Squap D4d -- -- -- 8 16 10 2 8{3}+2{4}
Antiprisme pentagonal 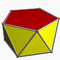Pentagonal antiprism.png P |2 2 5 Pentagonal antiprism vertfig.png
3.3.3.5		 Pap D5d -- U77 K02 10 20 12 2 10{3}+2{5}
Antiprisme hexagonal 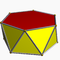Hexagonal antiprism.png P |2 2 6 Hexagonal antiprism vertfig.png
3.3.3.6		 Hap D6d -- -- -- 12 24 14 2 12{3}+2{6}
Antiprisme octogonal 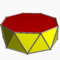Octagonal antiprism.png P |2 2 8 Octagonal antiprism vertfig.png
3.3.3.8		 Oap D8d -- -- -- 16 32 18 2 16{3}+2{8}
Antiprisme décagonal 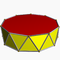Decagonal antiprism.png P |2 2 10 Decagonal antiprism vf.png
3.3.3.10		 Dap D10d -- -- -- 20 40 22 2 20{3}+2{10}
Antiprisme dodécagonal Dodecagonal antiprism.png P |2 2 12 Dodecagonal antiprism vf.png
3.3.3.12		 Twap D12d -- -- -- 24 48 26 2 24{3}+2{12}
Cuboctaèdre Cuboctahedron.png A 2|3 4 Cuboctahedron vertfig.png
3.4.3.4		 Co Oh W011 U07 K12 12 24 14 2 8{3}+6{4}
Petit rhombicuboctaèdre Small rhombicuboctahedron.png A 3 4|2 Small rhombicuboctahedron vertfig.png
3.4.4.4		 Sirco Oh W013 U10 K15 24 48 26 2 8{3}+(6+12){4}
Petit rhombicosidodécaèdre Small rhombicosidodecahedron.png A 3 5|2 Small rhombicosidodecahedron vertfig.png
3.4.5.4		 Srid Ih W014 U27 K32 60 120 62 2 20{3}+30{4}+12{5}
Petit pavage rhombitrihexagonal Uniform tiling 63-t02.png T 3 6|2 Small rhombitrihexagonal tiling vertfig.png
3.4.6.4		 Rothat p6m -- -- -- 6n 12n 6n 0 2n{3}+3n{4}+n{6}
Icosidodécaèdre Icosidodecahedron1.png A 2|3 5 Icosidodecahedron vertfig.png
3.5.3.5		 Id Ih W012 U24 K29 30 60 32 2 20{3}+12{5}
Pavage trihexagonal Uniform tiling 63-t1.png T 2|3 6 Trihexagonal tiling vertfig.png
3.6.3.6		 That p6m -- -- -- 3n 6n 3n 0 2n{3}+n{6}
Pavage triheptagonal Uniform tiling 73-t1.png T 2|3 6 3.7.3.7 -- *732 -- -- -- 3n 6n 3n 0 2n{3}+n{7}
Pavage carré Uniform tiling 44-t0.png T 4|2 4 Square tiling vertfig.png
4.4.4.4		 Squat p4m -- -- -- n 2n n 0 n{4}

Formes convexes (5 faces/sommet)

Nom Image Classe de
solide		 Symbole de
Wythoff		 Figure de sommet Acronyme
de Bowers		 Groupe de
symétrie		 W# U# K# Sommets Arêtes Faces Chi Faces par type
Icosaèdre Icosahedron.png R 5|2 3 Icosahedron vertfig.png
3.3.3.3.3		 Ike Ih W004 U22 K27 12 30 20 2 20{3}
Cube adouci Snub hexahedron.png A |2 3 4 Snub cube vertfig.png
3.3.3.3.4		 Snic O W017 U12 K17 24 60 38 2 (8+24){3}+6{4}
Dodécaèdre adouci Snub dodecahedron ccw.png A |2 3 5 Snub dodecahedron vertfig.png
3.3.3.3.5		 Snid I W018 U29 K34 60 150 92 2 (20+60){3}+12{5}
Pavage hexagonal adouci Uniform tiling 63-snub.png T |2 3 6 Snub hexagonal tiling vertfig.png
3.3.3.3.6		 Snathat p6 -- -- -- 6n 15n 9n 0 8n{3}+n{6}
Pavage triangulaire allongé Tile 33344.svg T |2 2 (2|2) Tiling 33344-vertfig.png
3.3.3.4.4		 Etrat cmm -- -- -- 2n 5n 3n 0 2n{3}+n{4}
Pavage carré adouci Uniform tiling 44-snub.png T |2 4 4 Snub square tiling vertfig.png
3.3.4.3.4		 Snasquat p4g -- -- -- 4n 10n 6n 0 4n{3}+2n{4}

Formes convexes (6 faces/sommet)

Nom Image Classe de
solide		 Symbole de
Wythoff		 Figure de sommet Acronyme
de Bowers		 Groupe de
symétrie		 W# U# K# Sommets Arêtes Faces Chi Faces par type
Pavage triangulaire Uniform tiling 63-t2.png T 6|2 3 Triangular tiling vertfig.png
3.3.3.3.3.3		 Trat p6m -- -- -- n 3n 2n 0 2n{3}

Formes convexes (7 faces/sommet)

Nom Image Classe de
solide		 Symbole de
Wythoff		 Figure de sommet Acronyme
de Bowers		 Groupe de
symétrie		 W# U# K# Sommets Arêtes Faces Chi Faces par type
Pavage triangulaire d'ordre 7 Uniform tiling 73-t2.png T 7|2 3 3.3.3.3.3.3.3 -- *732 -- -- -- n 3n 2n 0 2n{3}

Formes non-convexes avec des faces convexes

Nom Image Classe de
solide		 Symbole de
Wythoff		 Figure de sommet Acronyme
de Bowers		 Groupe de
symétrie		 W# U# K# Sommets Arêtes Faces Chi Faces par type
Tétrahémihexaèdre Tetrahemihexahedron.png C+ 3/2 3|2 Tetrahemihexahedron vertfig.png
4.3/2.4.3		 Thah Td W067 U04 K09 6 12 7 1 4{3}+3{4}
Cubohémioctaèdre Cubohemioctahedron.png C+ 4/3 4|3 Cubohemioctahedron vertfig.png
6.4/3.6.4		 Cho Oh W078 U15 K20 12 24 10 -2 6{4}+4{6}
Octahémioctaèdre Octahemioctahedron.png C+ 3/2 3|3 Octahemioctahedron vertfig.png
6.3/2.6.3		 Oho Oh W068 U03 K08 12 24 12 0 8{3}+4{6}
Grand dodécaèdre Great dodecahedron.png R+ 5/2|2 5 Great dodecahedron vertfig.png
(5.5.5.5.5)/2		 Gad Ih W021 U35 K40 12 30 12 -6 12{5}
Grand icosaèdre Great icosahedron.png R+ 5/2|2 3 Great icosahedron vertfig.png
(3.3.3.3.3)/2		 Gike Ih W041 U53 K58 12 30 20 2 20{3}
Grand icosidodécaèdre ditrigonal Great ditrigonal icosidodecahedron.png C+ 3/2|3 5 Great ditrigonal icosidodecahedron vertfig.png
(5.3.5.3.5.3)/2		 Gidtid Ih W087 U47 K52 20 60 32 -8 20{3}+12{5}
Petit rhombihexaèdre Small rhombihexahedron.png C+ 3/2 2 4| Small rhombihexahedron vertfig.png
4.8.4/3.8		 Sroh Oh W086 U18 K23 24 48 18 -6 12{4}+6{8}
Petit cubicuboctaèdre Small cubicuboctahedron.png C+ 3/2 4|4 Small cubicuboctahedron vertfig.png
8.3/2.8.4		 Socco Oh W069 U13 K18 24 48 20 -4 8{3}+6{4}+6{8}
Grand rhombicuboctaèdre uniforme Uniform great rhombicuboctahedron.png C+ 3/2 4|2 Uniform great rhombicuboctahedron vertfig.png
4.3/2.4.4		 Querco Oh W085 U17 K22 24 48 26 2 8{3}+(6+12){4}
Petit dodécahémidodécaèdre Small dodecahemidodecahedron.png C+ 5/4 5|5 Small dodecahemidodecahedron vertfig.png
10.5/4.10.5		 Sidhid Ih W091 U51 K56 30 60 18 -12 12{5}+6{10}
Petit icosihémidodécaèdre Small icosihemidodecahedron.png C+ 3/2 3|5 Small icosihemidodecahedron vertfig.png
10.3/2.10.3		 Seihid Ih W089 U49 K54 30 60 26 -4 20{3}+6{10}
Petit dodécicosaèdre Small dodecicosahedron.png C+ 3/2 3 5| Small dodecicosahedron vertfig.png
10.6.10/9.6/5		 Siddy Ih W090 U50 K55 60 120 32 -28 20{6}+12{10}
Petit rhombidodécaèdre Small rhombidodecahedron.png C+ 2 5/2 5| Small rhombidodecahedron vertfig.png
10.4.10/9.4/3		 Sird Ih W074 U39 K44 60 120 42 -18 30{4}+12{10}
Petit dodécicosidodécaèdre Small dodecicosidodecahedron.png C+ 3/2 5|5 Small dodecicosidodecahedron vertfig.png
10.3/2.10.5		 Saddid Ih W072 U33 K38 60 120 44 -16 20{3}+12{5}+12{10}
Rhombicosaèdre Rhombicosahedron.png C+ 2 5/2 3| Rhombicosahedron vertfig.png
6.4.6/5.4/3		 Ri Ih W096 U56 K61 60 120 50 -10 30{4}+20{6}
Grand icosicosidodécaèdre Great icosicosidodecahedron.png C+ 3/2 5|3 Great icosicosidodecahedron vertfig.png
6.3/2.6.5		 Giid Ih W088 U48 K53 60 120 52 -8 20{3}+12{5}+20{6}

Formes prismatiques non-convexes

Nom Image Classe de
solide		 Symbole de
Wythoff		 Figure de sommet Acronyme
de Bowers		 Groupe de
symétrie		 W# U# K# Sommets Arêtes Faces Chi Faces par type
Prisme pentagrammique Pentagrammic prism.png P+ 2 5/2|2 Pentagrammic prism vertfig.png
5/2.4.4		 Stip D5h -- U78 K03 10 15 7 2 5{4}+2{5/2}
Prisme heptagrammique (7/3) Heptagrammic prism 7-3.png P+ 2 7/3|2 Septagrammic prism-3-7 vertfig.png
7/3.4.4		 Giship D7h -- -- -- 14 21 9 2 7{4}+2{7/3}
Prisme heptagrammique (7/2) Heptagrammic prism 7-2.png P+ 2 7/2|2 Septagrammic prism vertfig.png
7/2.4.4		 Ship D7h -- -- -- 14 21 9 2 7{4}+2{7/2}
Antiprisme pentagrammique Pentagrammic antiprism.png P+ |2 2 5/2 Pentagrammic antiprism vertfig.png
5/2.3.3.3		 Stap D5h -- U79 K04 10 20 12 2 10{3}+2{5/2}
Antiprisme pentagrammique croisé Pentagrammic crossed antiprism.png P+ |2 2 5/3 Pentagrammic crossed-antiprism vertfig.png
5/3.3.3.3		 Starp D5d -- U80 K05 10 20 12 2 10{3}+2{5/2}

Autres formes non-convexes avec des faces non-convexes

Nom Image Classe de
solide		 Symbole de
Wythoff		 Figure de sommet Acronyme
de Bowers		 Groupe de
symétrie		 W# U# K# Sommets Arêtes Faces Chi Faces par type
Petit dodécaèdre étoilé Small stellated dodecahedron.png R+ 5|2 5/2 Small stellated dodecahedron vertfig.png
(5/2)5		 Sissid Ih W020 U34 K39 12 30 12 -6 12{5/2}
Grand dodécaèdre étoilé Great stellated dodecahedron.png R+ 3|2 5/2 Great stellated dodecahedron vertfig.png
(5/2)3		 Gissid Ih W022 U52 K57 20 30 12 2 12{5/2}
Dodécadodécaèdre ditrigonal Ditrigonal dodecadodecahedron.png S+ 3|5/3 5 Ditrigonal dodecadodecahedron vertfig.png
(5/3.5)3		 Ditdid Ih W080 U41 K46 20 60 24 -16 12{5}+12{5/2}
Petit icosidodécaèdre ditrigonal Small ditrigonal icosidodecahedron.png S+ 3|5/2 3 Small ditrigonal icosidodecahedron vertfig.png
(5/2.3)3		 Sidtid Ih W070 U30 K35 20 60 32 -8 20{3}+12{5/2}
Hexaèdre tronqué étoilé Stellated truncated hexahedron.png S+ 2 3|4/3 Stellated truncated hexahedron vertfig.png
8/3.8/3.3		 Quith Oh W092 U19 K24 24 36 14 2 8{3}+6{8/3}
Grand rhombihexaèdre Great rhombihexahedron.png S+ 4/33/2 2| Great rhombihexahedron vertfig.png
4.8/3.4/3.8/5		 Groh Oh W103 U21 K26 24 48 18 -6 12{4}+6{8/3}
Grand cubicuboctaèdre Great cubicuboctahedron.png S+ 3 4|4/3 Great cubicuboctahedron vertfig.png
8/3.3.8/3.4		 Gocco Oh W077 U14 K19 24 48 20 -4 8{3}+6{4}+6{8/3}
Grand dodécahémidodécaèdre Great dodecahemidodecahedron.png S+ 5/35/2|5/3 Great dodecahemidodecahedron vertfig.png
10/3.5/3.10/3.5/2		 Gidhid Ih W107 U70 K75 30 60 18 -12 12{5/2}+6{10/3}
Petit dodécahémicosaèdre Small dodecahemicosahedron.png S+ 5/35/2|3 Small dodecahemicosahedron vertfig.png
6.5/3.6.5/2		 Sidhei Ih W100 U62 K67 30 60 22 -8 12{5/2}+10{6}
Grand dodécahémicosaèdre Great dodecahemicosahedron.png S+ 5/4 5|3 Great dodecahemicosahedron vertfig.png
6.5/4.6.5		 Gidhei Ih W102 U65 K70 30 60 22 -8 12{5}+10{6}
Dodécadodécaèdre Dodecadodecahedron.png S+ 2|5/2 5 Dodecadodecahedron vertfig.png
(5/2.5)2		 Did Ih W073 U36 K41 30 60 24 -6 12{5}+12{5/2}
Grand icosihémidodécaèdre Great icosihemidodecahedron.png S+ 3/2 3|5/3 Great icosihemidodecahedron vertfig.png
10/3.3/2.10/3.3		 Geihid Ih W106 U71 K76 30 60 26 -4 20{3}+6{10/3}
Grand icosidodécaèdre Great icosidodecahedron.png S+ 2|5/2 3 Great icosidodecahedron vertfig.png
(5/2.3)2		 Gid Ih W094 U54 K59 30 60 32 2 20{3}+12{5/2}
Cuboctaèdre cubitronqué Cubitruncated cuboctahedron.png S+ 4/3 3 4| Cubitruncated cuboctahedron vertfig.png
8/3.6.8		 Cotco Oh W079 U16 K21 48 72 20 -4 8{6}+6{8}+6{8/3}
Grand cuboctaèdre tronqué Great truncated cuboctahedron.png S+ 4/3 2 3| Great truncated cuboctahedron vertfig.png
8/3.4.6		 Quitco Oh W093 U20 K25 48 72 26 2 12{4}+8{6}+6{8/3}
Grand dodécaèdre tronqué Great truncated dodecahedron.png S+ 2 5/2|5 Truncated great dodecahedron vertfig.png
10.10.5/2		 Tigid Ih W075 U37 K42 60 90 24 -6 12{5/2}+12{10}
Petit dodécaèdre étoilé tronqué Small stellated truncated dodecahedron.png S+ 2 5|5/3 Small stellated truncated dodecahedron vertfig.png
10/3.10/3.5		 Quitsissid Ih W097 U58 K63 60 90 24 -6 12{5}+12{10/3}
Grand dodécaèdre étoilé tronqué Great stellated truncated dodecahedron.png S+ 2 3|5/3 Great stellated truncated dodecahedron vertfig.png
10/3.10/3.3		 Quitgissid Ih W104 U66 K71 60 90 32 2 20{3}+12{10/3}
Grand icosaèdre tronqué Great truncated icosahedron.png S+ 2 5/2|3 Great truncated icosahedron vertfig.png
6.6.5/2		 Tiggy Ih W095 U55 K60 60 90 32 2 12{5/2}+20{6}
Grand dodécicosaèdre Great dodecicosahedron.png S+ 5/35/2 3| Great dodecicosahedron vertfig.png
6.10/3.6/5.10/7		 Giddy Ih W101 U63 K68 60 120 32 -28 20{6}+12{10/3}
Grand rhombidodécaèdre Great rhombidodecahedron.png S+ 3/25/3 2| Great rhombidodecahedron vertfig.png
4.10/3.4/3.10/7		 Gird Ih W109 U73 K78 60 120 42 -18 30{4}+12{10/3}
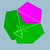
Icosidodécadodécaèdre Icosidodecadodecahedron.png S+ 5/3 5|3 Icosidodecadodecahedron vertfig.png
6.5/3.6.5		 Ided Ih W083 U44 K49 60 120 44 -16 12{5}+12{5/2}+20{6}
Petit dodécicosidodécaèdre ditrigonal 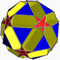Small ditrigonal dodecicosidodecahedron.png S+ 5/3 3|5 Small ditrigonal dodecicosidodecahedron vertfig.png
10.5/3.10.3		 Sidditdid Ih W082 U43 K48 60 120 44 -16 20{3}+12{;5/2}+12{10}
Grand dodécicosidodécaèdre ditrigonal Great ditrigonal dodecicosidodecahedron.png S+ 3 5|5/3 Great ditrigonal dodecicosidodecahedron vertfig.png
10/3.3.10/3.5		 Gidditdid Ih W081 U42 K47 60 120 44 -16 20{3}+12{5}+12{10/3}
Grand dodécicosidodécaèdre Great dodecicosidodecahedron.png S+ 5/2 3|5/3 Great dodecicosidodecahedron vertfig.png
10/3.5/2.10/3.3		 Gaddid Ih W099 U61 K66 60 120 44 -16 20{3}+12{5/2}+12{10/3}
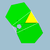
Petit icosicosidodécaèdre Small icosicosidodecahedron.png S+ 5/2 3|3 Small icosicosidodecahedron vertfig.png
6.5/2.6.3		 Siid Ih W071 U31 K36 60 120 52 -8 20{3}+12{5/2}+20{6}
Rhombidodécadodécaèdre Rhombidodecadodecahedron.png S+ 5/2 5|2 Rhombidodecadodecahedron vertfig.png
4.5/2.4.5		 Raded Ih W076 U38 K43 60 120 54 -6 30{4}+12{5}+12{5/2}
Grand rhombicosidodécaèdre uniforme Uniform great rhombicosidodecahedron.png S+ 5/3 3|2 Uniform great rhombicosidodecahedron vertfig.png
4.5/3.4.3		 Qrid Ih W105 U67 K72 60 120 62 2 20{3}+30{4}+12{5/2}
Dodécadodécaèdre adouci Snub dodecadodecahedron.png S+ |2 5/2 5 Snub dodecadodecahedron vertfig.png
3.3.5/2.3.5		 Siddid I W111 U40 K45 60 150 84 -6 60{3}+12{5}+12{5/2}
Dodécadodécaèdre adouci inversé Inverted snub dodecadodecahedron.png S+ |5/3 2 5 Inverted snub dodecadodecahedron vertfig.png
3.5/3.3.3.5		 Isdid I W114 U60 K65 60 150 84 -6 60{3}+12{5}+12{5/2}
Grand icosidodécaèdre adouci Great snub icosidodecahedron.png S+ |2 5/2 3 Great snub icosidodecahedron vertfig.png
3.4.5/2		 Gosid I W116 U57 K62 60 150 92 2 (20+60){3}+12{5/2}
Grand icosidodécaèdre adouci inversé Great inverted snub icosidodecahedron.png S+ |5/3 2 3 Great inverted snub icosidodecahedron vertfig.png
3.3.5/3		 Gisid I W113 U69 K74 60 150 92 2 (20+60){3}+12{5/2}
Grand icosidodécaèdre rétroadouci Great retrosnub icosidodecahedron.png S+ |3/25/3 2 Great retrosnub icosidodecahedron vertfig.png
(34.5/2)/2		 Girsid I W117 U74 K79 60 150 92 2 (20+60){3}+12{5/2}
Grand dodécicosidodécaèdre adouci Great snub dodecicosidodecahedron.png S+ |5/35/2 3 Great snub dodecicosidodecahedron vertfig.png
33.5/3.3.5/2		 Gisdid I W115 U64 K69 60 180 104 -16 (20+60){3}+(12+12){5/2}
Icosidodécadodécaèdre adouci Snub icosidodecadodecahedron.png S+ |5/3 3 5 Snub icosidodecadodecahedron vertfig.png
3.3.5.5/3		 Sided I W112 U46 K51 60 180 104 -16 (20+60){3}+12{5}+12{5/2}
Petit icosicosidodécaèdre adouci Small snub icosicosidodecahedron.png S+ |5/2 3 3 Small snub icosicosidodecahedron vertfig.png
35.5/2		 Seside Ih W110 U32 K37 60 180 112 -8 (40+60){3}+12{5/2}
Petit icosicosidodécaèdre rétroadouci Small retrosnub icosicosidodecahedron.png S+ |3/23/25/2 Small retrosnub icosicosidodecahedron vertfig.png
(35.5/3)/2		 Sirsid Ih W118 U72 K77 60 180 112 -8 (40+60){3}+12{5/2}
Grand dirhombicosidodécaèdre Great dirhombicosidodecahedron.png S+ |3/25/3 3

5/2

 Great dirhombicosidodecahedron vertfig.png
(4.5/3.4.3.
4.5/2.4.3/2)/2		 Gidrid Ih W119 U75 K80 60 240 124 -56 40{3}+60{4}+24{5/2}
Dodécadodécaèdre icositronqué 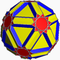Icositruncated dodecadodecahedron.png S+ 5/3 3 5| Icositruncated dodecadodecahedron vertfig.png
10/3.6.10		 Idtid Ih W084 U45 K50 120 180 44 -16 20{6}+12{10}+12{10/3}
Dodécadodécaèdre tronqué Truncated dodecadodecahedron.png S+ 5/3 2 5| Truncated dodecadodecahedron vertfig.png
10/3.4.10		 Quitdid Ih W098 U59 K64 120 180 54 -6 30{4}+12{10}+12{10/3}
Grand icosidodécaèdre tronqué Great truncated icosidodecahedron.png S+ 5/3 2 3| Great truncated icosidodecahedron vertfig.png
10/3.4.6		 Gaquatid Ih W108 U68 K73 120 180 62 2 30{4}+20{6}+12{10/3}

Cas particulier

Nom Image Classe de
solide		 Symbole de
Wythoff		 Figure de sommet Acronyme
de Bowers		 Groupe de
symétrie		 W# U# K# Sommets Arêtes Faces Chi Faces par type
Grand dirhombidodécaèdre disadouci
Polyèdre de Skilling		 Great disnub dirhombidodecahedron.png S++ | (3/2) 5/3 (3) 5/2 Great disnub dirhombidodecahedron vertfig.png
(5/2.4.3.3.3.4. 5/3.4.3/2.3/2.3/2.4)/2		 -- Ih -- -- -- 60 240 (*1) 204 24 120{3}+60{4}+24{5/2}

(*1) : Le grand dirhombidodécaèdre disadouci possède 120 arêtes partagées par quatre faces. Si elles sont comptées comme deux paires, alors il existe au total 360 arêtes. À cause de cette dégénérescence des arêtes, il n'est pas toujours considéré comme un polyèdre uniforme.

Renvois

  • Classes de solides
    • R = 5 solides de Platon
    • R+= 4 solides de Kepler-Poinsot
    • A = 13 solides d'Archimède
    • C+= 14 polyèdres non-convexes avec des faces convexes (tous ces polyèdres uniformes ont les faces qui se coupent les unes les autres)
    • S+= 39 polyèdres non-convexes avec des faces complexes (étoilées)
    • P = Série infinie des prismes réguliers convexes et des antiprismes
    • P+= Série infinie des prisme et des antiprismes uniformes non-convexes (ceux-ci contiennent tous des faces complexes (étoiles))
    • T = 11 pavages planaires
  • Acronyme de Bowers - Un nom unique abrégé prononçable basé sur l'anglais créé par le mathématicien Jonathan Bowers
  • Indexation uniforme : U01-U80 (d'abord le tétraèdre, les prisme à 76+)
  • Indexation Kaleido : K01-K80 <K(n)=U(n-5) pour n=6..80> (prismes 1-5, Tétraèdre 6+)
  • Magnus Wenninger Patrons de polyèdre : W001-W119
    • 1-18 - 5 convexes réguliers et 13 convexes semi-réguliers
    • 20-22, 41 - 4 non-convexes réguliers
    • 19-66 48 stellations/composés spéciaux (Non-réguliers non données sur cette liste)
    • 67-119 - 53 non-convexes uniformes
  • Chi: la caractéristique d'Euler, χ. Les pavages uniformes sur le plan correspondent à une topologie torique, avec une caractéristique d'Euler égale à zéro.
  • Pour les pavages du plan, les nombres donnés de sommets, d'arêtes et de faces montrent le ratio de tels éléments dans une période du motif, qui, dans chaque cas, est un losange (quelquefois un losange à angle droit, i.e. un carré).
  • Note sur les images de figure de sommet :
    • Les droites blanches de polygone représentent la "figure de sommet" du polygone. Les faces colorées incluses sur les images des figures de sommet aident à voir leurs relations.

Liens externes


Solides géométriques
Les polyèdres
Les solides de Platon
Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre
Les solides d'Archimède
Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre
Les solides de Kepler-Poinsot
Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre
Les solides de Catalan
Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre
Les solides de Johnson
Les solides de révolution
Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Liste des poly%C3%A8dres uniformes ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Liste Des Polyèdres Uniformes de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Liste des polyedres uniformes — Liste des polyèdres uniformes Les polyèdres uniformes et les pavages forment un groupe bien étudié. Ils sont listés ici pour une comparaison rapide de leurs propriétés et de leurs noms de schéma variés ainsi que de leurs symboles. Cette liste… …   Wikipédia en Français

  • Liste des polyèdres uniformes — Cette liste recense les polyèdres uniformes, ainsi que certaines de leurs propriétés. Sommaire 1 Méthodologie 2 Table des polyèdres 2.1 Formes convexes (3 faces/sommet) …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Polyèdre uniforme — Un polyèdre uniforme (en) est un polyèdre qui a pour faces des polygones réguliers et tel qu il existe une isométrie qui applique un sommet quelconque sur un autre. Il en découle que tous les sommets sont congruents, et que le polyèdre… …   Wikipédia en Français

  • Polyedre uniforme — Polyèdre uniforme Un polyèdre uniforme est un polyèdre qui a pour faces des polygones réguliers et peut passer d un sommet à l autre (i.e. il existe une isométrie qui applique un sommet quelconque sur un autre. Il en découle que tous les sommets… …   Wikipédia en Français

  • Symbole de wythoff — Exemple des triangles de construction de Wythoff avec les 7 points générateurs. Les droites des miroirs actifs sont colorés en rouge, jaune et bleu avec les 3 noeuds qui leur sont opposés associés par le symbole de Wythoff. En géométrie, un… …   Wikipédia en Français

  • Symbole de Wythoff — Exemple des triangles de construction de Wythoff avec les 7 points générateurs. Les droites des miroirs actifs sont colorés en rouge, jaune et bleu avec les 3 noeuds qui leur sont opposés associés par le symbole de Wythoff. En géométrie, un… …   Wikipédia en Français

  • Diagramme de Coxeter-Dynkin — Les groupes de Coxeter dans le plan avec les diagrammes équivalents. Les miroirs du domaine sont nommés par les arêtes m1, m2, etc. Les sommets sont colorés par leur ordre de réflexion. Le groupe prismatique [W2xW2] est montré comme un doublement …   Wikipédia en Français

  • Solide d'Archimede — Solide d Archimède En géométrie, un solide d Archimède est un polyèdre convexe semi régulier, fortement symétrique composé de deux sortes (ou davantage) de polygones réguliers se rencontrant à des sommets identiques. Ils sont distincts des… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”