- Icositetraedre trapezoidal
-
Icositétraèdre trapézoïdal
Icositétraèdre trapézoïdal 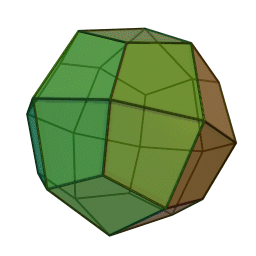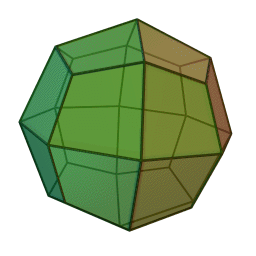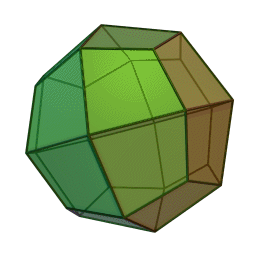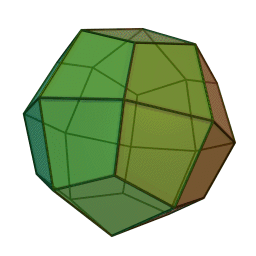
Type Solide de Catalan Faces Cerf-volants Éléments :
· Faces
· Arêtes
· Sommets
· Caractéristique
24
48
26
2Faces par sommet 3 et 5 Sommets par face 4 Isométries Octaédrique Dual Petit rhombicuboctaèdre Propriétés Convexe, uniformité des faces Un icositétraèdre trapézoïdal est un solide de Catalan qui ressemble un peu à un cube gonflé de l'intérieur. Son polyèdre dual est le petit rhombicuboctaèdre.
Les 24 faces sont des cerf-volants, pas des trapèzes; le trapèzoèdre est mal nommé de manière similaire.
L'icositétraèdre trapézoïdal est une structure cristalline souvent formée par le minéral analcime et occasionnellement par le grenat. La forme est souvent appelée un trapèzoèdre dans les contextes minéralogiques, bien qu'en géométrie du solide, ce nom fait référence à une classe particulière de polyèdres.
Le Trapézoèdre brillant du mythe de fiction de Lovecraft a été probablement prévu pour se référer à un cristal de cette forme.
Voir aussi
Références
- Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979, ISBN 0-486-23729-X
Solides géométriques Les polyèdres Les solides de Platon Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre Les solides d'Archimède Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre Les solides de Kepler-Poinsot Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre Les solides de Catalan Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre Les solides de Johnson Les solides de révolution Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution - Portail de la géométrie
Catégorie : Polyèdre
Wikimedia Foundation. 2010.
