Tetrakihexaedre

Tetrakihexaedre

Tétrakihexaèdre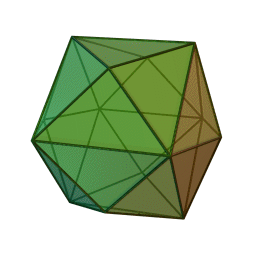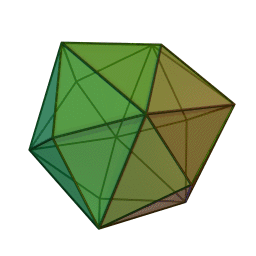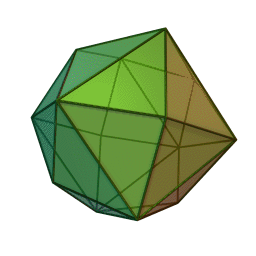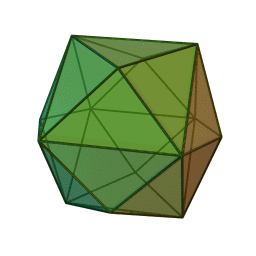

Tétrakihexaèdre
Tétrakihexaèdre
Type Solide de Catalan
Faces Triangles isocèles
Éléments :
 · Faces
 · Arêtes
 · Sommets
 · Caractéristique		  
24
36
14
2
Faces par sommet 4 et 6
Sommets par face 3
Isométries Octaédrique
Dual Octaèdre tronqué
Propriétés Convexe, uniformité des faces

Un tétrakihexaèdre est un dual de solide d'Archimède, ou un solide de Catalan. Son dual est l'octaèdre tronqué.

Il peut être vu comme un cube avec des pyramides carrées (de hauteur 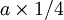a \times 1/4) couvrant chaque face. Cette interprétation est exprimée dans le nom (hexaèdre=cube tétraki=faces partagées en 4 triangles).


Sommaire

Longueurs, surface et volume

Le rapport entre les longueurs des deux types d'arêtes est de 3 / 4.

Si la grande arête (celle du squelette cubique) a pour longueur "a" :

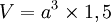
Son volume vaut : V = a^3 \times 1,5

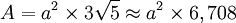
Sa surface vaut : A = a^2 \times 3\sqrt{5} \approx a^2 \times 6,708


Si jamais on agrandit les pyramides, de sorte à ce que tous les triangles deviennent équilatéraux, la polyèdre n'est plus convexe ni inscriptible dans une sphère, mais est régulier ; toutes ses arêtes sont de longueur "a", on a alors :

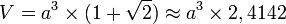
Son volume qui vaut : V = a^3 \times (1+\sqrt{2}) \approx a^3 \times 2,4142

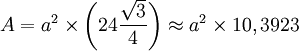
Sa surface qui vaut : A = a^2 \times \biggl(24 \frac{\sqrt{3}}{4} \biggl) \approx a^2 \times 10,3923

Applications humaines et naturelles

Des dés polyédriques ayant la forme de tétrakihexaèdres sont occasionnellement utilisés par des joueurs.

Des formations cristallines naturelles de tétrakihexaèdres sont observées dans le cuivre et la fluorine.


Références

  • Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979, ISBN 0-486-23729-X
  • Sur le site Mathworld

Voir aussi

Articles connexes

Liens externes


Solides géométriques
Les polyèdres
Les solides de Platon
Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre
Les solides d'Archimède
Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre
Les solides de Kepler-Poinsot
Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre
Les solides de Catalan
Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre
Les solides de Johnson
Les solides de révolution
Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « T%C3%A9trakihexa%C3%A8dre ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Tetrakihexaedre de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Tétrakihexaèdre — Type Solide de Catalan Faces Triangles isocèles Éléments :  · Faces  · Arêtes  · Sommets  …   Wikipédia en Français

  • Dé à vingt-quatre faces — 4 dé à 24 faces. Les dés à 24 faces sont très rarement utilisés, mais ils sont désignés par « D24 » lorsqu ils sont utilisés au sein d un jeu. Description du dé …   Wikipédia en Français

  • Solide de Catalan — Un dodécaèdre rhombique En mathématiques, un solide de Catalan ou dual archimédien, est un polyèdre dual d un solide d Archimède. Les solides de Catalan ont été nommés ainsi en l honneur du mathématicien belge Eugène Catalan qui fut le premier à… …   Wikipédia en Français

  • Solide de catalan — Un dodécaèdre rhombique En mathématiques, un solide de Catalan ou dual archimédien, est un polyèdre dual d un solide d Archimède. Les solides de Catalan ont été nommés ainsi en l honneur du mathématicien belge Eugène Catalan qui fut le premier à… …   Wikipédia en Français

  • Deltaedre — Deltaèdre Le tétraèdre tronqué avec des hexagones remplacés par des triangles n est pas un deltaèdre convexe parce qu il n est pas strictement convexe. Un deltaèdre est un polyèdre dont toutes les faces sont des triangles équilatéraux. Le nom est …   Wikipédia en Français

  • Deltaèdre — Le tétraèdre tronqué avec des hexagones remplacés par des triangles n est pas un deltaèdre convexe parce qu il n est pas strictement convexe. Un deltaèdre est un polyèdre dont toutes les faces sont des triangles équilatéraux. Le nom est issu de… …   Wikipédia en Français

  • Dual D'un Polyèdre — En géométrie, il existe plusieurs façons (géométrique, combinatoire) de mettre les polyèdres en dualité. Dans chaque cas, à tout polyèdre est associé un polyèdre appelé dual du premier, de telle sorte que le dual du polyèdre dual est le polyèdre… …   Wikipédia en Français

  • Dual d'un polyedre — Dual d un polyèdre En géométrie, il existe plusieurs façons (géométrique, combinatoire) de mettre les polyèdres en dualité. Dans chaque cas, à tout polyèdre est associé un polyèdre appelé dual du premier, de telle sorte que le dual du polyèdre… …   Wikipédia en Français

  • Dual d'un polyèdre — Pour les articles homonymes, voir Dualité (mathématiques) et Dualité. En géométrie, il existe plusieurs façons (géométrique, combinatoire) de mettre les polyèdres en dualité. Dans chaque cas, à tout polyèdre est associé un polyèdre appelé dual du …   Wikipédia en Français

  • Octaedre tronque — Octaèdre tronqué Octaèdre tronqué Type Solide d Archimède Faces Carrés et hexagones Éléments :  · Faces  · Arêtes  · Sommets  · Caractéristique   14 36 24 2 Faces par sommet …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”