- Triaki-icosaedre
-
Triaki-icosaèdre
Triaki-icosaèdre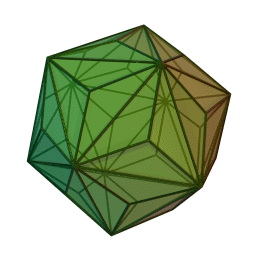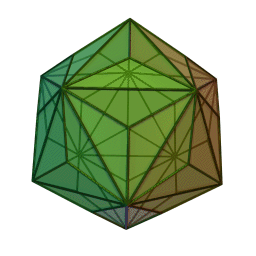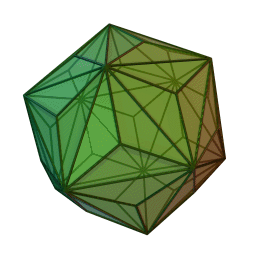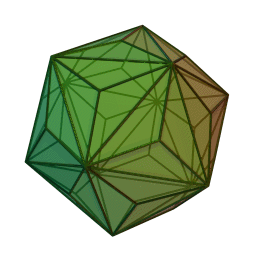 
Type Solide de Catalan Faces Triangles isocèles Éléments :
· Faces
· Arêtes
· Sommets
· Caractéristique
60
90
32
2Faces par sommet 3 et 10 Sommets par face 3 Isométries Icosaédrique Dual Dodécaèdre tronqué Propriétés Convexe, uniformité des faces Un triaki-icosaèdre est un polyèdre dual d'un solide d'Archimède, ou un solide de Catalan. Son dual est le dodécaèdre tronqué.
Il peut être vu comme un icosaèdre avec des pyramides triangulaires ajoutées sur chaque face. Cette interprétation est exprimée dans le nom.
Cette interprétation peut aussi être associée avec d'autres polyèdres non-convexes similaires avec des pyramides de différentes hauteurs :
Première stellation de l'icosaèdre (quelquefois appelé un triaki-icosaèdre)
Grand dodécaèdre étoilé (avec de très grandes pyramides)
Grand dodécaèdre (avec des pyramides inversées)
Voir aussi
- Pavage triakitriangulaire pour d'autres formes polyédriques "triakis".
Références
- Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979, ISBN 0-486-23729-X
- Magnus Wenninger, Polyhedron Models, Cambridge University Press, 1974, ISBN 0-521-09859-9
Solides géométriques Les polyèdres Les solides de Platon Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre Les solides d'Archimède Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre Les solides de Kepler-Poinsot Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre Les solides de Catalan Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre Les solides de Johnson Les solides de révolution Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution 
Portail de la géométrie
Catégorie : Polyèdre
Wikimedia Foundation. 2010.
