Hexakioctaedre

Hexakioctaedre

Hexakioctaèdre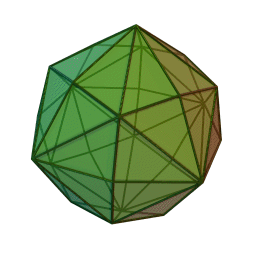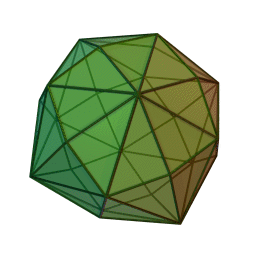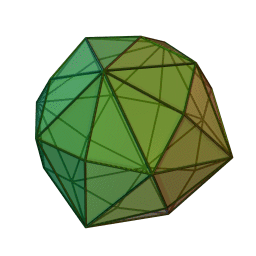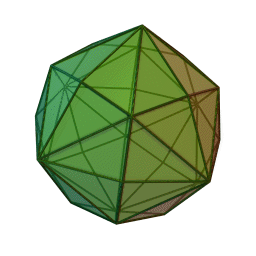

Hexakioctaèdre
Hexakioctaèdre trapézoïdal
Type Solide de Catalan
Faces Triangles scalènes
Éléments :
 · Faces
 · Arêtes
 · Sommets
 · Caractéristique		  
48
72
26
2
Faces par sommet 4 et 6
Sommets par face 3
Isométries Octaédrique
Dual Grand rhombicuboctaèdre
Propriétés Convexe, uniformité des faces

Un hexakioctaèdre est un solide de Catalan et le dual du solide d'Archimède, le grand rhombicuboctaèdre. Comme tel, il est de faces uniformes mais avec des faces polygonales irrégulières. Il ressemble un peu à un dodécaèdre rhombique gonflé— si on remplace chaque face d'un dodécaèdre rhombique avec un sommet unique et quatre triangles d'une manière régulière, on a pour résultat un hexakioctaèdre.

Voir aussi

Références

  • Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979, ISBN 0-486-23729-X

Lien externe


Solides géométriques
Les polyèdres
Les solides de Platon
Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre
Les solides d'Archimède
Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre
Les solides de Kepler-Poinsot
Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre
Les solides de Catalan
Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre
Les solides de Johnson
Les solides de révolution
Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Hexakiocta%C3%A8dre ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Hexakioctaedre de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Hexakioctaèdre — Type Solide de Catalan Faces Triangles scalènes Éléments :  · Faces  · Arêtes  · So …   Wikipédia en Français

  • Solide de Catalan — Un dodécaèdre rhombique En mathématiques, un solide de Catalan ou dual archimédien, est un polyèdre dual d un solide d Archimède. Les solides de Catalan ont été nommés ainsi en l honneur du mathématicien belge Eugène Catalan qui fut le premier à… …   Wikipédia en Français

  • Solide de catalan — Un dodécaèdre rhombique En mathématiques, un solide de Catalan ou dual archimédien, est un polyèdre dual d un solide d Archimède. Les solides de Catalan ont été nommés ainsi en l honneur du mathématicien belge Eugène Catalan qui fut le premier à… …   Wikipédia en Français

  • Cuboctaèdre Tronqué — Type Solide d Archimède Faces Hexagones, Octogones et Carrés Éléments :  · Faces  · Arêtes  · Sommets  · Caractéristique   26 72 48 2 …   Wikipédia en Français

  • Cuboctaèdre tronqué — Type Solide d Archimède Faces Hexagones, Octogones et Carrés Éléments  …   Wikipédia en Français

  • Dual D'un Polyèdre — En géométrie, il existe plusieurs façons (géométrique, combinatoire) de mettre les polyèdres en dualité. Dans chaque cas, à tout polyèdre est associé un polyèdre appelé dual du premier, de telle sorte que le dual du polyèdre dual est le polyèdre… …   Wikipédia en Français

  • Dual d'un polyedre — Dual d un polyèdre En géométrie, il existe plusieurs façons (géométrique, combinatoire) de mettre les polyèdres en dualité. Dans chaque cas, à tout polyèdre est associé un polyèdre appelé dual du premier, de telle sorte que le dual du polyèdre… …   Wikipédia en Français

  • Dual d'un polyèdre — Pour les articles homonymes, voir Dualité (mathématiques) et Dualité. En géométrie, il existe plusieurs façons (géométrique, combinatoire) de mettre les polyèdres en dualité. Dans chaque cas, à tout polyèdre est associé un polyèdre appelé dual du …   Wikipédia en Français

  • Grand Rhombicuboctaèdre — Cuboctaèdre tronqué Cuboctaèdre Tronqué Type Solide d Archimède Faces Hexagones, Octogones et Carrés Éléments :  · Faces  · Arêtes  · Sommets  · Caractéristique   26 72 48 2 …   Wikipédia en Français

  • Grand rhombicuboctaedre — Cuboctaèdre tronqué Cuboctaèdre Tronqué Type Solide d Archimède Faces Hexagones, Octogones et Carrés Éléments :  · Faces  · Arêtes  · Sommets  · Caractéristique   26 72 48 2 …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”