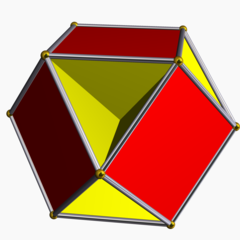
Cubohemioctaedre
- Cubohemioctaedre
-
Cubohémioctaèdre
En géométrie, le Cubohémioctaèdre est un polyèdre uniforme non-convexe, indexé sous le nom U15.
Un polyèdre non-convexe a des faces qui se coupent qui ne représentent pas de nouvelles arêtes ou de nouvelles faces. Les 4 hexagones dans ce modèle passent tous à travers le centre du modèle. Les hexagones se coupent les uns les autres et seules des portions triangulaires sont visibles.
Les 12 sommets et les 24 arêtes, le long desquelles se trouvent les 6 faces carrées, coïncident avec le cuboctaèdre convexe.
Liens externes
Site mathcurve
 Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Cubohemioctaedre de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Cubohémioctaèdre — Type Polyèdre uniforme Éléments F=10, A=24, S=12 (χ= 2) Faces par côtés 6{4}+4{6} Configuration de sommet 4.6.4/3 … Wikipédia en Français
Liste Des Polyèdres Uniformes — Les polyèdres uniformes et les pavages forment un groupe bien étudié. Ils sont listés ici pour une comparaison rapide de leurs propriétés et de leurs noms de schéma variés ainsi que de leurs symboles. Cette liste inclut : tous les 75… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Liste des polyedres uniformes — Liste des polyèdres uniformes Les polyèdres uniformes et les pavages forment un groupe bien étudié. Ils sont listés ici pour une comparaison rapide de leurs propriétés et de leurs noms de schéma variés ainsi que de leurs symboles. Cette liste… … Wikipédia en Français
Liste des polyèdres uniformes — Cette liste recense les polyèdres uniformes, ainsi que certaines de leurs propriétés. Sommaire 1 Méthodologie 2 Table des polyèdres 2.1 Formes convexes (3 faces/sommet) … Wikipédia en Français
Polyèdre uniforme — Un polyèdre uniforme (en) est un polyèdre qui a pour faces des polygones réguliers et tel qu il existe une isométrie qui applique un sommet quelconque sur un autre. Il en découle que tous les sommets sont congruents, et que le polyèdre… … Wikipédia en Français
Relation d'Euler — Théorème de Descartes Euler Le théorème de Descartes Euler (ou relation d Euler), formulé par Leonhard Euler en 1752, énonce une formule mathématique qui relie le nombre de côtés, de sommets, et de faces dans un polyèdre du genre 0. Un polyèdre… … Wikipédia en Français
Theoreme de Descartes-Euler — Théorème de Descartes Euler Le théorème de Descartes Euler (ou relation d Euler), formulé par Leonhard Euler en 1752, énonce une formule mathématique qui relie le nombre de côtés, de sommets, et de faces dans un polyèdre du genre 0. Un polyèdre… … Wikipédia en Français
Théorème de Descartes-Euler — Le théorème de Descartes Euler (ou relation d Euler), formulé par Leonhard Euler en 1752, énonce une formule mathématique qui relie le nombre de côtés, de sommets, et de faces dans un polyèdre de genre 0 (c est à dire, intuitivement, un polyèdre… … Wikipédia en Français
Théorème de descartes-euler — Le théorème de Descartes Euler (ou relation d Euler), formulé par Leonhard Euler en 1752, énonce une formule mathématique qui relie le nombre de côtés, de sommets, et de faces dans un polyèdre du genre 0. Un polyèdre de genre 0 est un polyèdre… … Wikipédia en Français