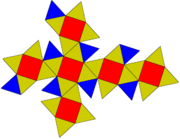
- Cube Adouci
-
Cube adouci
Cube adouci 
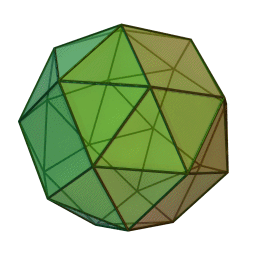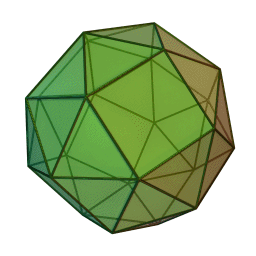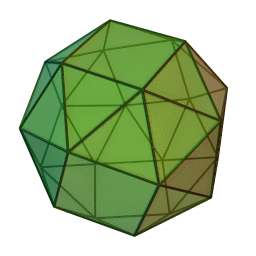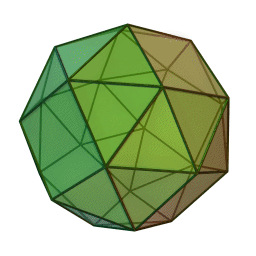
Type Solide d'Archimède Faces Triangles et carrés Éléments :
· Faces
· Arêtes
· Sommets
· Caractéristique
38
60
24
2Faces par sommet 5 Sommets par face 3 et 4 Isométries O Dual Icositétraèdre pentagonal Propriétés Semi-régulier et convexe, chiral Le cube adouci ou cuboctaèdre adouci est un solide d'Archimède.
Le cube adouci possède 38 faces dont 6 sont des carrés et les 32 autres sont des triangles équilatéraux. Il possède 60 arêtes et 24 sommets. Il a deux formes distinctes, qui sont leurs images dans un miroir (ou "énantiomorphes") l'un de l'autre.
Sommaire
Coordonnées cartésiennes
Les coordonnées cartésiennes pour un cube adouci sont toutes les permutations paires de
avec un nombre pair de signes plus, avec toutes les permutations impaires avec un nombre impair de signes plus, où ξ est la solution réelle de
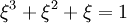 ,
,
qui peut être écrit
où approximativement 0,543689. En prenant les permutations paires avec un nombre impair de signes plus, et les permutations impaires avec un nombre pair de signes plus, on obtient un cube adouci différent, l'image miroir.
Relations géométriques
Le cube adouci peut être engendré en prenant les six faces du cube, en les tirant vers l'extérieur ainsi, elles ne se touchent plus. Puis, en leur donnant une petite rotation sur leur centres (toutes dans le sens horaire (Sh) ou antihoraire (Sah)) jusqu'à ce que les espaces entre elles puissent être remplis par des triangles équilatéraux.
Le cube adouci ne doit pas être confondu avec le cube tronqué.
Voir aussi
Références
- Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979, ISBN 0-486-23729-X
Liens externes
- (en) Les polyèdres uniformes
- (en) Les polyèdres en réalité virtuelle L'encyclopédie des Polyèdres
Solides géométriques Les polyèdres Les solides de Platon Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre Les solides d'Archimède Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre Les solides de Kepler-Poinsot Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre Les solides de Catalan Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre Les solides de Johnson Les solides de révolution Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution - Portail de la géométrie
Catégorie : Polyèdre
Wikimedia Foundation. 2010.

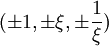
![\xi = \frac{1}{3}\left(\sqrt[3]{17+\sqrt{297}} - \sqrt[3]{-17+\sqrt{297}} - 1\right)](/pictures/frwiki/56/832fa68469f91dbf778028386c8c002e.png)