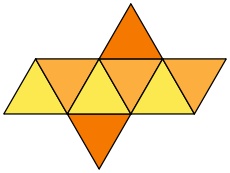
- Octaèdre régulier
-
Octaèdre 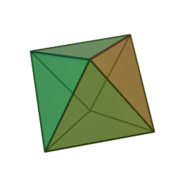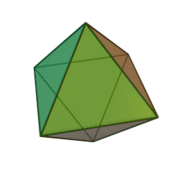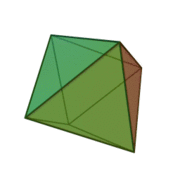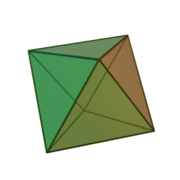
Type Polyèdre régulier Faces Triangle Éléments :
· Faces
· Arêtes
· Sommets
· Caractéristique
8
12
6
2Faces par sommet 4 Sommets par face 3 Isométries Dual Cube Propriétés Deltaèdre régulier et convexe modifier 
Un octaèdre régulier est un solide de Platon composé de huit faces dont chacune est un triangle équilatéral, se joignant quatre à quatre à chaque sommet. Platon, dans ses travaux, a voulu expliquer la matière par cinq éléments, et a utilisé des polyèdres réguliers pour les symboliser, l'octaèdre représentait l'élément « air »[1].
L'aire A et le volume V de l'octaèdre régulier d'arête a valent respectivement :
L'octaèdre régulier est un genre spécial d'antiprisme triangulaire et de bipyramide carrée.
C'est aussi le dual du cube, c'est-à-dire que c'est le polyèdre obtenu en prenant pour sommets les centres des faces d'un cube, et en joignant les sommets qui correspondent à des faces adjacentes. En conséquence, on peut faire correspondre aux sommets et aux faces de l'octaèdre les faces et les sommets du cube.
Les coordonnées canoniques pour les sommets d'un octaèdre centré à l'origine sont (±1,0,0), (0, ±1, 0), (0,0,±1).
Comme il a trois sommets par face, et quatre faces par sommet, son symbole de Schläfli est {3,4}.
Le squelette de l'octaèdre régulier, l'ensemble de ses sommets reliés par ses arêtes, forme un graphe appelé graphe octaédrique.
Sommaire
L'octaèdre dans la vie courante
Dans les jeux
Article détaillé : dé à 8 faces.L'octaèdre régulier est utilisé comme dé à jouer, particulièrement dans les jeux de rôle
En cristallographie
Certains cristaux comme la fluorine forment un octaèdre régulier
Notes et références
- Les cinq éléments de Platon : Histoire du solide de Platon
Lien externe
Wikimedia Foundation. 2010.