- Solide de revolution
-
Solide de révolution
Un solide de révolution est engendré par une surface plane fermée tournant autour d'un axe situé dans la même plan qu'elle et ne possédant en commun avec elle aucun point ou seulement des points de sa frontière.
Parmi les solides de révolution, on peut citer :
- la boule
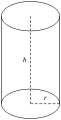
- le cylindre circulaire droit
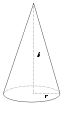
- le cône circulaire droit
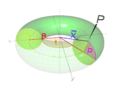
- le tore
- l'ellipsoïde (de révolution)
Tout plan contenant l'axe de rotation découpe sur la surface de révolution un méridien. Tout plan perpendiculaire à l'axe de rotation découpe sur la surface de révolution un cercle parallèle.
Les droites normales à la surface et s'appuyant sur un même cercle parallèle engendre en général une surface conique sauf si le cercle est de rayon maximal, auquel cas la surface est un plan, et sauf si le cercle est obtenu par un plan tangent à la surface de révolution, auquel cas la surface générée est cylindrique.
La règle de Pappus (ou théorème de Guldin) permet de calculer le volume d'un solide de révolution connaissant le barycentre de la surface plane génératrice.
Solides géométriques Les polyèdres Les solides de Platon Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre Les solides d'Archimède Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre Les solides de Kepler-Poinsot Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre Les solides de Catalan Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre Les solides de Johnson Les solides de révolution Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution - Portail de la géométrie
Catégories : Forme géométrique | Cercle et sphère
Wikimedia Foundation. 2010.