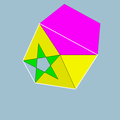
Dodecadodecaedre adouci
- Dodecadodecaedre adouci
-
Dodécadodécaèdre adouci
En géométrie, le dodécadodécaèdre adouci est un polyèdre uniforme non-convexe, indexé sous le nom U40.
Ce polyèdre peut être considéré comme un grand dodécaèdre adouci.
Coordonnées cartésiennes
Les coordonnées cartésiennes pour les sommets d'un dodécadodécaèdre adouci centré à l'origine sont toutes les permutations paires de
- (±2α, ±2, ±2β),
- (±(α+β/τ+τ), ±(-ατ+β+1/τ), ±(α/τ+βτ-1)),
- (±(-α/τ+βτ+1), ±(-α+β/τ-τ), ±(ατ+β-1/τ)),
- (±(-α/τ+βτ-1), ±(α-β/τ-τ), ±(ατ+β+1/τ)) et
- (±(α+β/τ-τ), ±(ατ-β+1/τ), ±(α/τ+βτ+1)),
avec un nombre pair de signes plus, où
- β = (α2/τ+τ)/(ατ−1/τ),
où τ = (1+√5)/2 est le nombre d'or (quelquefois écrit φ) et α est la solution réelle positive de τα4−α³+2α²−α−1/τ, ou approximativement 0,7964421. En prenant les permutations impaires des coordonnées ci-dessus avec un nombre impair de signes plus, cela donne une autre forme, l'énantiomorphe de ce polyèdre.
Voir aussi
Lien externe
 Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Dodecadodecaedre adouci de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Dodécadodécaèdre Adouci — Type Polyèdre uniforme Éléments F=84, A=150, S=60 (χ= 6) Faces par cotés 60{3}+12{5}+12{5/2} … Wikipédia en Français
Dodécadodécaèdre adouci — Type Polyèdre uniforme Éléments F=84, A=150, S=60 (χ= 6) Faces par côtés 60{3}+12{5}+12{5/2} Configuration de sommet … Wikipédia en Français
Dodecadodecaedre adouci inverse — Dodécadodécaèdre adouci inversé Dodécadodécaèdre inversé adouci Type Polyèdre uniforme Éléments F=84, A=150, S=60 (χ= 6) Faces par cotés 60{3}+12{5}+12{5/ … Wikipédia en Français
Dodécadodécaèdre Adouci Inversé — Dodécadodécaèdre inversé adouci Type Polyèdre uniforme Éléments F=84, A=150, S=60 (χ= 6) Faces par cotés 60{3}+12{5}+12{5/ … Wikipédia en Français
Dodécadodécaèdre adouci inversé — Dodécadodécaèdre inversé adouci Type Polyèdre uniforme Éléments F=84, A=150, S=60 (χ= 6) Faces par côtés 60{3}+12{5}+12{5/2} … Wikipédia en Français
Dodécadodécaèdre icositronqué — Type Polyèdre uniforme Éléments F=44, A=180, S=120 (χ= 16) Faces par côtés 20{6}+12{10}+12{10/3} … Wikipédia en Français
Dodécadodécaèdre tronqué — Dodécadodécaèdre icositronqué Type Polyèdre uniforme Éléments F=44, A=180, S=120 (χ= 16) Faces par côtés 20{6}+12{10}+12{10/3} … Wikipédia en Français
Dodécadodécaèdre — Type Polyèdre uniforme Éléments F=24, A=60, S=30 (χ= 6) Faces par côtés 12{5}+12{5/2} Configuration de sommet … Wikipédia en Français
Dodécadodécaèdre ditrigonal — Type Polyèdre uniforme Éléments F=24, A=60, S=20 (χ= 16) Faces par côtés 12{5}+12{5/2} Configurati … Wikipédia en Français
Dodecadodecaedre icositronque — Dodécadodécaèdre icositronqué Dodécadodécaèdre icositronqué Type Polyèdre uniforme Éléments F=44, A=180, S=120 (χ= 16) Faces par cotés 20{6}+12{10}+12{10/ … Wikipédia en Français