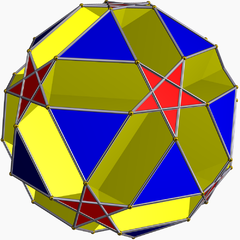
Petit dodecicosidodecaedre ditrigonal
Contenu soumis à la licence CC-BY-SA. Source : Article Petit dodecicosidodecaedre ditrigonal de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Petit dodécicosidodécaèdre ditrigonal — Type Polyèdre uniforme Éléments F=44, A=120, S=60 (χ= 16) Faces par côtés 20{3}+12{5/2}+12{10} … Wikipédia en Français
Grand Dodécicosidodécaèdre Ditrigonal — Type Polyèdre uniforme Éléments F=44, A=120, S=60 (χ= 16) Faces par cotés … Wikipédia en Français
Grand dodecicosidodecaedre ditrigonal — Grand dodécicosidodécaèdre ditrigonal Grand dodécicosidodécaèdre ditrigonal Type Polyèdre uniforme Éléments F=44, A=120, S=60 (χ= 16) Faces par cotés … Wikipédia en Français
Grand dodécicosidodécaèdre ditrigonal — Type Polyèdre uniforme Éléments F=44, A=120, S=60 (χ= 16) Faces par côtés 20{3}+12{5}+12{10/3} … Wikipédia en Français
Petit dodecicosaedre — Petit dodécicosaèdre Petit dodécicosaèdre Type Polyèdre uniforme Éléments F=32, A=120, S=60 (χ= 28) Faces par cotés 20{6}+12{10} Configuration de sommet … Wikipédia en Français
Petit icosicosidodecaedre — Petit icosicosidodécaèdre Petit icosicosidodécaèdre Type Polyèdre uniforme Éléments F=52, A=120, S=60 (χ= 8) Faces par cotés 20{3}+12{5/2}+20{6} … Wikipédia en Français
Petit dodécicosaèdre — Type Polyèdre uniforme Éléments F=32, A=120, S=60 (χ= 28) Faces par côtés 20{6}+12{10} Configuration de sommet 6 … Wikipédia en Français
Petit icosicosidodécaèdre — Type Polyèdre uniforme Éléments F=52, A=120, S=60 (χ= 8) Faces par côtés 20{3}+12{5/2}+20{6} Configuration … Wikipédia en Français
Liste Des Polyèdres Uniformes — Les polyèdres uniformes et les pavages forment un groupe bien étudié. Ils sont listés ici pour une comparaison rapide de leurs propriétés et de leurs noms de schéma variés ainsi que de leurs symboles. Cette liste inclut : tous les 75… … Wikipédia en Français
Liste des polyedres uniformes — Liste des polyèdres uniformes Les polyèdres uniformes et les pavages forment un groupe bien étudié. Ils sont listés ici pour une comparaison rapide de leurs propriétés et de leurs noms de schéma variés ainsi que de leurs symboles. Cette liste… … Wikipédia en Français