- Grand Dirhombidodécaèdre Disadouci
-
Grand dirhombidodécaèdre disadouci
Grand dirhombidodécaèdre disadouci 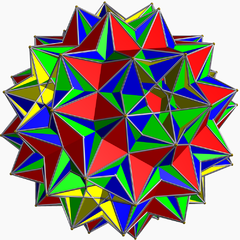
Type Polyèdre uniforme Éléments F=204, A=240, S=60 (χ=32) Faces par cotés 120{3}+60{4}+24{5/2} Configuration de sommet (5/2.4.3.3.3.4. 5/3.4.3/2.3/2.3/2.4)/2 Symbole de Wythoff | (3/2) 5/3 (3) 5/2 Groupe de symétrie Ih Références d'indexation U-, C-, W- 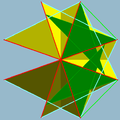
(5/2.4.3.3.3.4. 5/3.4.3/2.3/2.3/2.4)/2
(Figure de sommet)Fichier:Wideblank.png
Grand dirhombidodécacron disadouci
(Polyèdre dual)
En géométrie, le grand dirhombidodécaèdre disadouci, aussi appelé le polyèdre de Skilling, est un polyèdre uniforme non-convexe.John Skilling a découvert ce polyèdre uniforme supplémentaire, en assouplissant la condition que seules deux faces peuvent se rencontrer sur une arête. Certains auteurs ne le comptent pas comme un polyèdre uniforme, parce que certaines paires d'arêtes coïncident.
Il a 120 arêtes avec 2 faces et 120 arêtes avec 4 faces. Si les arêtes à 4 faces sont comptées deux fois, comme deux arêtes topologiquement disjointes, ce polyèdre peut être considéré comme ayant 360 arêtes au total, la caractéristique d'Euler devient -88.
Il partage les mêmes sommets et arêtes que le grand dirhombicosidodécaèdre, mais a un ensemble différent de faces triangulaires. Les sommets et les arêtes sont aussi partagées avec les composés uniformes de 20 octaèdres ou tétrahémihexaèdres. 180 arêtes sont partagées avec le grand dodécicosidodécaèdre adouci.
La figure de sommet a 4 faces carrées passant à travers le centre du modèle.
Références
- John Skilling, The complete set of uniform polyhedra. Philosophical Transactions of the Royal Society, Ser. A, 278, pp. 111-135, 1975
Voir aussi
Lien externe
- http://web.ukonline.co.uk/polyhedra/uniform/skilling.htm
- http://www.georgehart.com/virtual-polyhedra/great_disnub_dirhombidodecahedron.html
- Portail de la géométrie
Catégorie : Polyèdre
Wikimedia Foundation. 2010.
