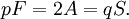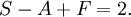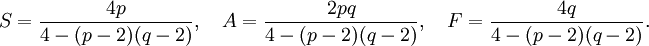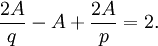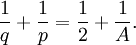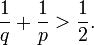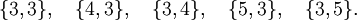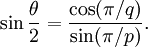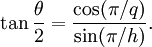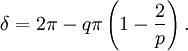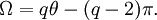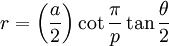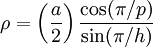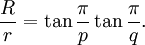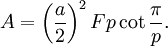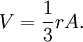Solide platonicien

Solide de Platon

En géométrie, un solide de Platon est un polyèdre régulier convexe. Ce sont les analogues tridimensionnels des polygones réguliers convexes. Il y a précisément cinq figures de cette sorte (montrées ci-dessous). Elles sont uniques dans le fait que les bords, les arêtes et les angles sont tous congrus.

Les cinq polyèdres réguliers convexes (solides de Platon)
Tétraèdre	Hexaèdre ou Cube	Octaèdre	Dodécaèdre	Icosaèdre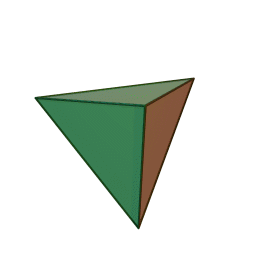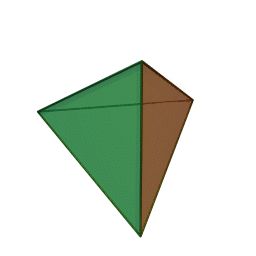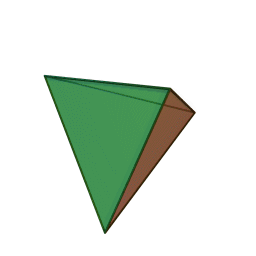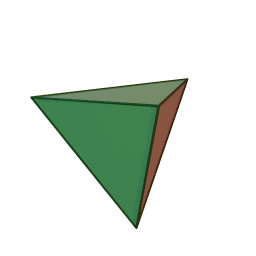

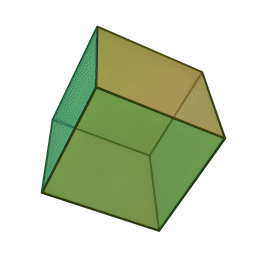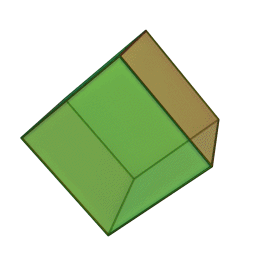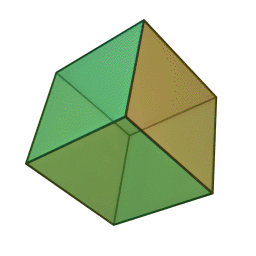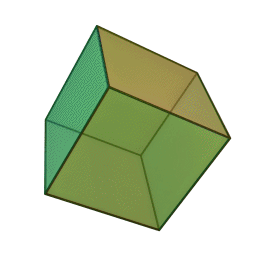
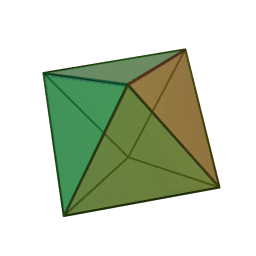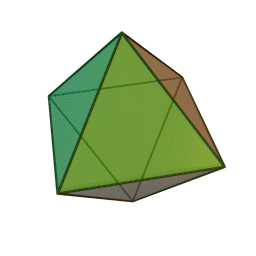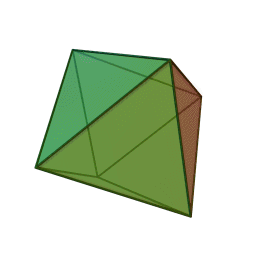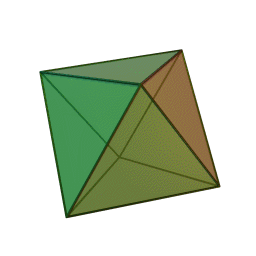
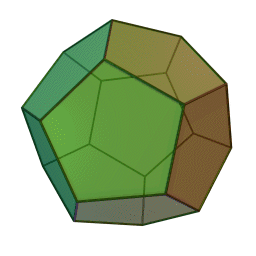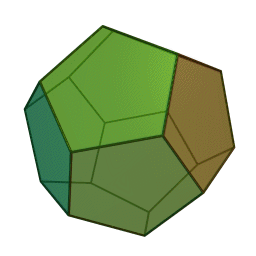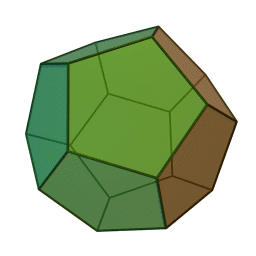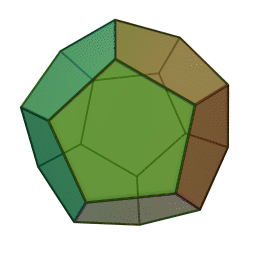
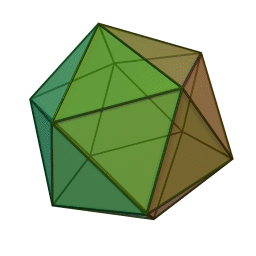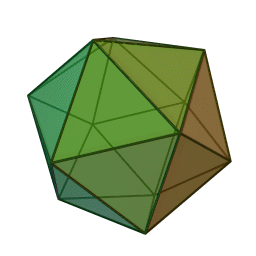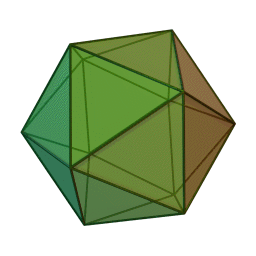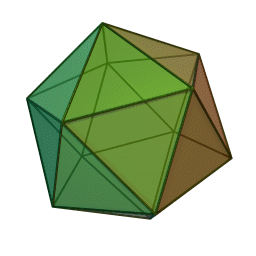
Le nom de chaque solide est dérivé du nombre des faces le composant : respectivement 4, 6, 8, 12 et 20. ^[1]

En raison de leur esthétisme et de leur symétrie, les solides de Platon ont été un sujet d'étude favori des géomètres depuis des milliers d'années. Ils ont été nommés en l'honneur du philosophe grec Platon qui fit la théorie énonçant que les Éléments physiques (les quatre éléments) ont été construits à partir des solides réguliers.

Histoire

Les peuples néolithiques d'Écosse ont construit des modèles en pierre des cinq solides au moins 1 000 ans avant Platon (Atiyah et Sutcliffe 2003). Ces modèles sont gardés au Ashmolean Museum à Oxford.

Dans l'histoire des mathématiques de la Grèce antique, on peut tracer la chronologie suivante. Les pythagoriciens ont eu une connaissance empirique de trois solides : le tétraèdre (la pyramide), l'hexaèdre (le cube), le dodécaèdre (douze faces). Qui exactement connaissait ? Selon Proclos, Pythagore lui-même (vers 530 av. J.-C.). Mais ce peut être son disciple Hippase de Métaponte, ou, plus vraisemblablement, Archytas de Tarente (vers 360 av. J.-C.). Peut-être Hippase a construit, le premier, le dodécaèdre. Il n'est pas fait mention de la pyramide avant Démocrite (fragment 155), actif vers 430 av. J.-C. Archytas aurait le premier construit le cube, pour résoudre le problème de la duplication du carré. Le premier, Platon mentionne le dodécaèdre, dans le Phédon (110b), qui date d'env. 383 av. J.-C. Le mathématicien Théétète d'Athènes (mort en 395 ou 360 av. J.-C.) a découvert les deux autres solides : l'octaèdre et l'icosaèdre ; surtout, il les a construits, le premier, tous les cinq.^[2] Platon a philosophé là-dessus.

Les solides de Platon joue un rôle premier dans la philosophie de Platon, à partir duquel ils ont été nommés. Platon, dans le dialogue Timée (env. 358 av. J.-C.), associait chacun des quatre Éléments physiques (la Terre, l'Air, l'Eau et le Feu) avec un solide régulier. La Terre était associée avec le cube (Timée, 55d), l'Air avec l'octaèdre, l'Eau avec l'icosaèdre et le Feu avec le tétraèdre. Il existait une justification pour ces associations : la chaleur du Feu semble pointue et comme un poignard (comme un peu le tétraèdre). L'Air est constitué de l'octaèdre ; ses composants minuscules sont si doux qu'on peut à peine les sentir. L'Eau, l'icosaèdre, s'échappe de la main lorsqu'on la saisit comme si elle était constituée de petites boules minuscules. Par contraste, un solide fortement sphérique, l'hexaèdre (cube) représente la Terre. Ces petits solides font de la poussière lorsqu'ils sont émiettés et se cassent lorsqu'on s'en saisit, une grande différence avec l'écoulement doux de l'eau. Pour le cinquième solide de Platon, le dodécaèdre, Platon remarque obscurément, "...le dieu utilisé pour arranger les constellations sur tout le ciel ". Platon mettait en correspondance le dodécaèdre avec le Tout (Phédon, 110b ; Timée, 55c), parce que c'est le solide qui ressemble le plus à la sphère. Aristote a nommé ce cinquième élément, aithêr (aether en Latin, "éther" en Français) et a postulé que l'univers était fait de cet élément, et qu'il était substantiel à tout les autres, qu'il les contenait tous.

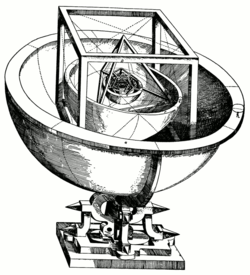Modèle du système solaire par des modèles de solides de Platon de Kepler issu du Mysterium Cosmographicum (1596)

Speusippe, le successeur de Platon à l'Académie (en 348 av. J.-C.) a repensé la tradition pythagoricienne sur les cinq solides (Pythagore, Hippase, Archytas).

Euclide a donné une description mathématique complète des solides de Platon dans les Éléments (env. 300 av. J.-C.) ; le dernier livre (Livre XIII) qui est consacré à leurs propriétés. Les propositions 13–17 dans le Livre XIII décrit la construction du tétraèdre, de l'octaèdre, du cube, de l'icosaèdre et du dodécaèdre dans cet ordre. Pour chaque solide, Euclide trouve le rapport du diamètre à la sphère circonscrite à la longueur des arêtes. Dans la proposition 18, il argumente qu'il n'existe pas plus de polyèdres réguliers convexes. Beaucoup des informations dans le Livre XIII est probablement dérivé du travail de Théétète.

Au XVI^e siècle, l'astronome allemand Johannes Kepler essaya de trouver une relation entre les cinq planètes connues à l'époque (en excluant la Terre) et les cinq solides de Platon. Dans le Mysterium Cosmographicum, publié en 1596, Kepler présenta un modèle de système solaire dans lequel les cinq solides étaient fixés les uns dans les autres et séparés par une série de sphères inscrites et circonscrites. Les six sphères correspondaient chacune aux planètes (Mercure, Vénus, la Terre, Mars, Jupiter et Saturne). Les solides étaient ordonnés de l'intérieur vers l'extérieur, le premier étant l'octaèdre, suivi de l'icosaèdre, du dodécaèdre, du tétraèdre et finalement le cube. De cette manière, la structure du système solaire et les relations de distances entre les planètes étaient dictées par les solides de Platon. Vers la fin, l'idée originale de Kepler a été abandonnée, mais de cette recherche émergèrent la découverte des solides de Kepler, la constatation que les orbites des planètes ne sont pas des cercles, et les lois du mouvement planétaire de Kepler pour lesquelles il est maintenant célèbre.

Propriétés combinatoires

Un polyèdre convexe est un solide de Platon si et seulement si

Toutes ses faces sont des polygones réguliers convexes congrus,
Aucune de ses faces ne se coupe, excepté sur les arêtes
Le même nombre de faces se rencontrent à chacun de ses sommets.

Chaque solide de Platon peut par conséquent être noté par un symbole {p, q} où

p = le nombre de cotés de chaque face (ou le nombre de sommet sur chaque face) et

q = le nombre de faces se rencontrant à chaque sommet (ou le nombre d'arêtes se rencontrant à chaque sommet).

Le symbole {p, q}, appelé le symbole de Schläfli, donne une description combinatoire du polyèdre. Les symboles de Schläfli des cinq solides de Platon sont donnés dans la table ci-dessous.

Polyèdre	Sommets	Arêtes	Faces	Symbole de Schläfli	de sommet
Tétraèdre	4	6	4	{3, 3}	3.3.3
Hexaèdre	8	12	6	{4, 3}	4.4.4
Octaèdre	6	12	8	{3, 4}	3.3.3.3
Dodécaèdre	20	30	12	{5, 3}	5.5.5
Icosaèdre	12	30	20	{3, 5}	3.3.3.3.3

Toutes les autres informations combinatoires à propos de ces solides, telles que le nombre total de sommets (S), des arêtes (A) et des faces (F) peuvent être déterminées à partir de p et q. Puisque toute arête joint deux sommets et possède deux faces adjacentes, nous devons avoir :

$pF = 2A = qS.\,$

L'autre relation entre ces valeurs est donnée par la formule d'Euler :

$S - A + F = 2.\,$

Ce fait non-trivial peut être démontré d'une grande variété de manières (en topologie algébrique il découle de ce fait que la caractéristique d'Euler de la sphère est 2). Mises ensemble, ces trois relations déterminent complètement S, A et F :

$S = \frac{4p}{4 - (p-2)(q-2)},\quad A = \frac{2pq}{4 - (p-2)(q-2)},\quad F = \frac{4q}{4 - (p-2)(q-2)}.$

Note : échanger p et q intervertit F et S laissant A inchangé (pour une interprétation géométrique de ce fait, voir la section sur les polyèdres duaux ci-dessous).

Classification

C'est un résultat classique qu'il existe seulement cinq polyèdres réguliers convexes. Deux arguments communs sont donnés ci-dessous. Les deux montrent seulement qu'il ne peut pas y avoir plus de cinq solides de Platon. Que chacun des cinq existe réellement est une question séparée — à laquelle on peut répondre par une construction explicite.

Démonstration géométrique

L'argument géométrique suivant est très similaire à celui donné par Euclide dans les Éléments :

Chaque sommet du solide doit coïncider avec un sommet sur au moins trois faces, sinon ce n'est qu'un point de côté et non un sommet.
À chaque sommet du solide, le total des angles entre les cotés adjacents relatifs aux faces adjacentes, doit être inférieur à 360°.
Les angles de tous les sommets de toutes les faces d'un solide de Platon sont identiques, donc chaque sommet de chaque face doit contribuer pour moins de 360°/3=120°.
Les polygones réguliers de six cotés ou plus ont seulement des angles de 120° ou plus, donc la face commune doit être le triangle, le carré ou le pentagone. Et pour :
- les faces triangulaires : chaque sommet d'un triangle régulier a un angle de 60°, donc une forme doit avoir 3, 4 ou 5 triangles se rencontrant à un sommet ; celles-ci sont le tétraèdre, l'octaèdre et l'icosaèdre respectivement.
- les faces carrées : chaque sommet d'un carré a un angle de 90°, donc il existe seulement un arrangement possible avec trois faces à un sommet, le cube.
- les faces pentagonales : chaque sommet a un angle de 108° ; de nouveau, seulement un arrangement, de trois faces à un sommet est possible, le dodécaèdre.

Démonstration topologique

Une démonstration purement topologique peut être donnée en utilisant seulement les informations combinatoires sur les solides. La clé est l'observation d'Euler que $S - A + F = 2$ , et le fait que $p F = 2 A = q S$ . En combinant ces équations, on obtient l'équation

$\frac{2A}{q} - A + \frac{2A}{p} = 2.$

Une simple manipulation algébrique donne alors

${1 \over q} + {1 \over p}= {1 \over 2} + {1 \over A}.$

Puisque $A$ est strictement positif, nous devons avoir

$\frac{1}{q} + \frac{1}{p} > \frac{1}{2}.$

En utilisant le fait que p et q doivent, tous deux, être au moins égaux à 3, on peut facilement voir qu'il existe seulement cinq possibilités pour {p, q} :

$\{3, 3\},\quad \{4, 3\},\quad \{3, 4\},\quad \{5, 3\},\quad \{3,5\}.$

Propriétés géométriques

Angles

Il existe un nombre d'angles associés avec chaque solide de Platon. L'angle diédral est l'angle interne entre deux faces planes quelconques. L'angle diédral, θ, du solide {p,q} est donné par la formule

$\sin{\theta\over 2} = \frac{\cos(\pi/q)}{\sin(\pi/p)}.$

Ceci est quelquefois exprimé de manière plus pratique en termes de tangente par

$\tan{\theta\over 2} = \frac{\cos(\pi/q)}{\sin(\pi/h)}.$

La quantité h est 4, 6, 6, 10 et 10 pour le tétraèdre, le cube, l'octaèdre, le dodécaèdre et l'icosaèdre respectivement.

La déficience angulaire au sommet d'un polyèdre est la différence entre la somme des angles d'une face et 2π. La déficience, δ, à un sommet quelconque des sommets de Platons {p,q} est

$\delta = 2\pi - q\pi\left(1-{2\over p}\right).$

Par le théorème de Descartes, ceci est égal à 4π divisé par le nombre de sommets (i.e. la déficience totale de tous les sommets est 4π).

L'analogue tridimensionnel d'un angle plan est un angle solide. L'angle solide, Ω, au sommet d'un solide de Platon est donné en termes d'angle diédral par

$\Omega = q\theta - (q-2)\pi.\,$

Ceci provient de la formule de l'excès sphérique pour un polygone sphérique et le fait que la figure de sommet du polyèdre {p,q} est un q-gone régulier.

Les divers angles associés avec les solides de Platon sont donnés ci-dessous. Les valeurs numériques des angles solides sont données en stéradians. La constante 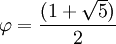$\varphi = \frac{(1+\sqrt{5})}{2}\,$ est le nombre d'or.

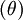
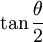
Polyèdre	Angle diédral $(\theta)\,$	$\tan\frac{\theta}{2}$	Déficience 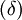$(\delta)\,$	Angle solide 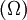$(\Omega)\,$
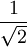
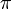
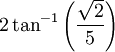
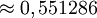
Tétraèdre	70,53°	$1\over{\sqrt 2}$	$\pi\,$	$2\tan^{-1}\left(\frac{\sqrt 2}{5}\right)$	$\approx 0,551286$
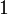
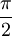
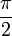
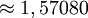
Cube	90°	$1\,$	$\pi\over 2$	$\frac{\pi}{2}$	$\approx 1,57080$
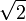
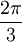
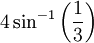
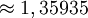
Octaèdre	109,47°	$\sqrt 2$	${2\pi}\over 3$	$4\sin^{-1}\left({1\over 3}\right)$	$\approx 1,35935$
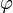
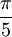
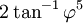
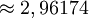
Dodécaèdre	116,56°	$\varphi\,$	$\pi\over 5$	$2\tan^{-1}\varphi^5$	$\approx 2,96174$
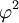
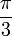
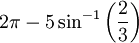
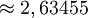
Icosaèdre	138,19°	$\varphi^2\,$	$\pi\over 3$	$2\pi - 5\sin^{-1}\left({2\over 3}\right)$	$\approx 2,63455$

Rayons, aires et volumes

Une autre vertu de la régularité est que les solides de Platon possèdent tous trois sphères concentriques :

la sphère circonscrite qui passe à travers tous les sommets,
la sphère moyenne qui est tangente à chaque arête au milieu de celle-ci et
la sphère inscrite qui est tangente à chaque face au centre de celle-ci.

Les rayons de ces sphères sont appelés les rayons circonscrits, les rayons moyens et les rayons internes. Ceux-ci sont les distances à partir du centre du polyèdre aux sommets, aux milieux des arêtes et aux centres de faces respectivement. Le rayon circonscrit R et le rayon interne r du solide {p, q} avec une longueur d'arête a sont donnés par

$R = \left({a\over 2}\right)\tan\frac{\pi}{q}\tan\frac{\theta}{2}$

$r = \left({a\over 2}\right)\cot\frac{\pi}{p}\tan\frac{\theta}{2}$

où θ est l'angle dièdre. Le rayon moyen ρ est donné par

$\rho = \left({a\over 2}\right)\frac{\cos(\pi/p)}{\sin(\pi/h)}$

où h est la quantité utilisée ci-dessus dans la définition de l'angle dièdre (h = 4, 6, 6, 10 ou 10). Noter que le rapport du rayon circonscrit au rayons interne est symétrique dans p et q :

${R\over r} = \tan\frac{\pi}{p}\tan\frac{\pi}{q}.$

La superficie A d'un solide de Platon {p, q} est facilement calculée, c'est l'aire d'un p-gone régulier fois le nombre de faces F. C’est-à-dire :

$A = \left({a\over 2}\right)^2 Fp\cot\frac{\pi}{p}.$

Le volume est calculé comme étant F fois le volume de la pyramide dont la base est un p-gone régulier et dont la hauteur est le rayon interne r. C’est-à-dire :

$V = {1\over 3}rA.$

Le tableau suivant liste les divers rayons des solides de Platon ainsi que leurs surfaces et leurs volumes. La taille globale est fixée en prenant la longueur d'arête, a, égale à 2.

Polyèdre (a = 2)	r	ρ	R	A	V
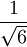
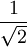
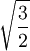
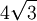
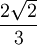
Tétraèdre	$1\over {\sqrt 6}$	$1\over {\sqrt 2}$	$\sqrt{3\over 2}$	$4\sqrt 3$	$\frac{2\sqrt 2}{3}$
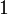
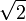
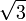
Cube	$1\,$	$\sqrt 2$	$\sqrt 3$	$24\,$	$8\,$
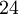
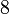
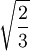
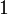
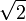
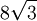
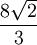
Octaèdre	$\sqrt{2\over 3}$	$1\,$	$\sqrt 2$	$8\sqrt 3$	$\frac{8\sqrt 2}{3}$
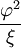
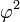
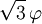
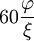
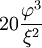
Dodécaèdre	$\frac{\varphi^2}{\xi}$	$\varphi^2$	$\sqrt 3\,\varphi$	$60\frac{\varphi}{\xi}$	$20\frac{\varphi^3}{\xi^2}$
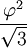
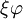
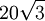
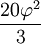
Icosaèdre	$\frac{\varphi^2}{\sqrt 3}$	$\varphi$	$\xi\varphi$	$20\sqrt 3$	$\frac{20\varphi^2}{3}$

Les constantes φ et ξ ci-dessus sont données par

$\varphi = 2\cos{\pi\over 5} = \frac{1+\sqrt 5}{2}\qquad\xi = 2\sin{\pi\over 5} = \sqrt{\frac{5-\sqrt 5}{2}} = 5^{1/4}\varphi^{-1/2}.$

Parmi les solides de Platon, le dodécaèdre ou l'icosaèdre peuvent être regardés comme la meilleure approximation de la sphère. L'icosaèdre a le plus grand nombre de face, le plus grand angle dièdre, et son enveloppe est la plus proche de sa sphère inscrite. Le dodécaèdre, d'un autre coté, a la plus petite déflexion angulaire, le plus grand angle solide au sommet et il remplit le plus sa sphère circonscrite.

Symétrie

Polyèdre dual

Un dual cube-octaèdre.

Chaque polyèdre possède un polyèdre dual avec les faces et les sommets interchangés. Le dual de chaque solide de Platon est un autre solide de Platon, c’est-à-dire que nous pouvons arranger les cinq solides en paires duales.

Le tétraèdre est auto-dual (i.e. son dual est un autre tétraèdre).
Le cube et l'octaèdre forment une paire duale.
Le dodécaèdre et l'icosaèdre forme une paire duale.

Si un polyèdre possède un symbole de Schläfli {p, q}, alors son dual possède le symbole {q, p}. En effet, chaque propriété combinatoire d'un solide de Platon peut être interprétée comme une autre propriété combinatoire du dual.

Groupes de symétrie

En mathématiques, le concept de symétrie est étudié avec la notion de groupe mathématique. Chaque polyèdre possède un groupe de symétrie associé, qui est l'ensemble de toutes les transformations (isométries euclidiennes) qui laissent le polyèdre invariant. L'ordre du groupe de symétrie est le nombre de symétries du polyèdre. On fait souvent une distinction entre le groupe de symétrie total, qui inclut les réflexions, et le groupe de symétrie propre, qui inclut seulement les rotations.

Les groupes de symétrie des solides de Platon sont connus sous le nom de groupes polyédriques (qui sont une classe particulière des groupes de point en trois dimensions). Le haut degré de symétrie des solides de Platon peut être interprété de différentes manières. Pour la plus importante, les sommets de chaque sommet sont tous équivalents sous l'action du groupe de symétrie, comme sont les arêtes et les faces. On dit que l'action du groupe de symétrie est transitive sur les sommets, les arêtes et les faces. En fait, c'est une autre manière de définir la régularité d'un polyèdre : un polyèdre est régulier si et seulement s'il est de sommet uniforme, d'arête uniforme et de face uniforme.

Il existe seulement trois groupes de symétrie associés avec les solides de Platon plutôt que cinq, puisque le groupe de symétrie d'un polyèdre quelconque coïncide avec celui de son dual. Ceci est vu facilement en examinant la construction du polyèdre dual. Toute symétrie de l'original doit être une symétrie du dual et vice-versa. Les trois groupes polyédriques sont :

Le groupe tétraédrique T,
Le groupe octaédrique O (qui est aussi le groupe de symétrie du cube), et
Le groupe icosaédrique I (qui est aussi le groupe de symétrie du dodécaèdre).

Les ordres des groupes propres (rotation) sont 12, 24 et 60 respectivement — précisément, deux fois le nombre des arêtes dans le polyèdre respectif. Les ordres des groupes de symétrie totaux sont deux fois de nouveau les ordres précédents (24, 48 et 120). Voir (Coxeter 1973) pour une déduction de ces faits.

Le tableau suivant liste les diverses propriétés de symétrie des solides de Platon. Les groupes de symétrie listés sont les groupes totaux avec les sous-groupes de rotation donnés entre parenthèses (comme pour le nombre de symétries). La construction kaléidoscopique de Wythoff est une méthode pour la construction des polyèdres directement à partir des groupes de symétrie. Nous listons la référence du symbole de Wythoff pour chaque solide de Platon.

Polyèdre	Symbole de Schläfli	Symbole de Wythoff	Polyèdre dual	Symétries	Groupe de symétrie
Tétraèdre	{3, 3}	3 \| 2 3	Tétraèdre	24 (12)	)
Cube	{4, 3}	3 \| 2 4	Octaèdre	48 (24)	)
Octaèdre	{3, 4}	4 \| 2 3	Cube	48 (24)	)
Dodécaèdre	{5, 3}	3 \| 2 5	Icosaèdre	120 (60)	)
Icosaèdre	{3, 5}	5 \| 2 3	Dodécaèdre	120 (60)	)

En nature et en technologie

Le tétraèdre, le cube et l'octaèdre apparaissent tous naturellement dans les structures cristallines. Ceux-ci épuisent nullement les nombres de formes possibles de cristaux. Néanmoins, ni l'icosaèdre régulier, ni le dodécaèdre régulier ne figurent parmi eux. Une de ces formes, appelée le pyritoèdre (nommé en rapport avec le groupe des minéraux avec lequel il est typique) a douze faces pentagonales, arrangées avec le même motif que les faces du dodécaèdre régulier. Néanmoins, les faces du pyritoèdre ne sont pas régulières, donc, le pyritoèdre n'est pas non plus régulier.

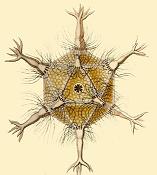Circogonia icosahedra, une espèce de radiolaire, formée comme un icosaèdre régulier.

Au début du XX^e siècle, Ernst Haeckel décrivit (Haeckel, 1904) de nombreuses d'espèces de Radiolaires, certaines comportant des squelettes ayant la forme de divers polyèdres réguliers. Ses exemples incluent Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus et Circorrhegma dodecahedra. Les formes de ces crétures étant évidentes d'après leurs noms.

Beaucoup de virus, tel que le virus de l'herpès, ont la forme d'un icosaèdre régulier. Les structures virales sont construites sur des sous-utités de protéines identiques répétées et l'icosaèdre est la forme la plus facile pour assembler en utilisant ces sous-unités. Un polyèdre régulier est utilisé car il peut être construit à partir d'une unité de protéine basique utilisée indéfiniment, ceci engendre un espace dans le génome viral.

En météorologie et en climatologie, les modèles numériques globaux des flux atmosphériques sont d'un intérêt croissant. Ils emploient des grilles qui sont basées sur un icosaèdre (raffiné par triangulation) à la place de la grille longitude/latitude plus communément utilisée. Ceci a l'avantage d'avoir une résolution spatiale également distribuée sans singularités (i.e. les pôles géographiques) aux dépens d'une certaine difficulté numérique plus grande.

La géométrie des armatures d'espace est souvent basée sur les solides de Platon. Dans le système MERO, les solides de Platon sont utilisés pour la convention de nomenclature des diverses configurations d'armatures d'espace. Par exemple ½O+T fait référence à une configuration faite d'un demi-octaèdre et un tétraèdre.

Les solides de Platon sont souvent utilisés pour fabriquer des dés. Les dés à 6 faces sont très communs, mais les autres nombres sont communément utilisés dans les jeux de rôle. De tels dés sont souvent appelés dn où n est le nombre de faces (d8, d20, etc.);

Article détaillé : dé.

Les dés polyèdriques sont souvent utilisés dans les jeux de rôle.

Ces formes apparaissent fréquemment dans d'autres jeux ou d'autres puzzles. Des puzzles similaires aux Rubik's Cube ont vu le jour dans toutes ces formes — voir polyèdres magiques.

Polyèdres reliés et polytopes

Polyèdres uniformes

Il existe quatre polyèdres réguliers qui ne sont pas convexes, appelés les solides de Kepler-Poinsot. Ceux-ci ont tous la symétrie icosaèdrique et peuvent être obtenus par stellations du dodécaèdre et de l'icosaèdre.

Fichier:CubOctahedron.svg
Cuboctaèdre

Icosidodécaèdre

Les prochains polyèdres convexes les plus réguliers après les solides de Platon sont le cuboctaèdre, qui est une rectification du cube et de l'octaèdre, et l'icosidodécaèdre, qui est une rectification du dodécaèdre et de l'icosaèdre (la rectification du polyèdre auto-dual, le tétraèdre est un octaèdre régulier). Ils sont tous les deux quasi-réguliers ce qui signifie qu'ils sont de sommet et d'arête uniformes et qu'ils ont des faces régulières, mais les faces ne sont pas toutes congrues (provenant de deux classes différentes). Ils forment deux des treize solides d'Archimède, qui sont des polyèdres uniformes convexes avec une symétrie polyèdrique.

Les polyèdres uniformes forment une classe beaucoup plus grande de polyèdres. Ces solides sont de sommets uniformes et on un ou plusieurs types de polygones réguliers ou étoilés pour faces. Ceux-ci incluent tous les polyèdres mentionnés ci-dessus avec l'ensemble infini des prismes, l'ensemble infini des antiprismes ainsi que 53 autres formes non-convexes.

Les solides de Johnson sont des polyèdres convexes qui ont des faces régulières mais qui ne sont pas uniformes.

Pavages

Les trois pavages réguliers du plan sont fortement reliés aux solides de Platon. En effet, on peut regarder les solides de Platon comme les cinq pavages réguliers de la sphère. Ceci est effectué en projetant chaque solide sur une sphère concentrique. Les faces projettent sur des polygones sphériques réguliers qui couvrent exactement la sphère. On peut montrer que chaque pavage régulier de la sphère est caractérisé par une paire d'entiers {p, q} avec 1/p + 1/q > 1/2. De même, un pavage régulier du plan est caractérisé par la condition 1/p + 1/q = 1/2. Il existe trois possibilités :

{4, 4} qui est le pavage carré,
{3, 6} qui est le pavage triangulaire et
{6, 3} qui est le pavage hexagonal (dual du pavage triangulaire).

D'une manière similaire, on peut considérer les pavages réguliers sur le plan hyperbolique. Ils sont caractérisés par la condition 1/p + 1/q < 1/2. Il existe un nombre infini de tels pavages.

Dimensions plus élevées

Lorsqu'il y a plus de trois dimensions, les polyèdres se généralisent aux polytopes. Dans le milieu du XIX^e siècle, le mathématicien suisse Ludwig Schläfli découvrit les analogues quadri-dimensionnels des solides de Platon, appelés les 4-polytopes réguliers convexes. Il existe exactement six de ces figures; cinq sont analogues aux solides de Platon, tandis que le sixième, le 24-cellules, n'a pas d'analogue en dimension inférieure.

Dans les dimensions plus élevées que quatre, il existe seulement trois polytopes réguliers convexes : le simplexe, l'hypercube et le polytope croisé. En trois dimensions, ceux-ci coïncident avec le tétraèdre, le cube et l'octaèdre.

Notes et références

↑ Dans le contexte de la géométrie du solide, le mot régulier est implicite et généralement omis. Le mot irrégulier est aussi utilisé pour souligner le fait qu'un polyèdre n'est pas régulier, bien qu'il soit encore supposé avoir la même topologie que la forme régulière. D'autres formes topologiques très différentes, telles que le dodécaèdre rhombique qui possède 12 faces rhombiques, ou un polyèdre étoilé non-convexe, comme le grand dodécaèdre, ne sont jamais donné avec des noms raccourcis.
↑ Eva Sachs, Die fünf platonischen Körper, Berlin, 1917. Festugière, Etudes de philosophie grecque, p. 385.

Voir aussi

Bibliographie

Sources

Platon, Timée (vers 358 av. J.-C.), 55e-56c. Trad. L. Brisson, Timée/Critias, Garnier-Flammarion, 3° éd. revue 1996.
Euclide, Éléments (vers 300 av. J.-C.), livre XIII. Euclide, Les Éléments, volume IV, Livre XI-XIII, Géométrie des solides ; trad. du texte par Heiberg et commentaires par Bernard Vitrac. Paris : Presses universitaires de France, 2001. (Bibliothèque d'histoire des sciences). 482 p. (ISBN 2-13-051927-X).

Études

Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. (1998); Art forms in nature, Prestel USA. ISBN 3-7913-1990-6, ou en ligne sur [1].

Liens externes

Information de solides de Platon
Travail Personnel Encadré sur les solides de Platon
Animation de solides de Platon
Livre XIII des Éléments d'Euclide.
Polyèdre 3D interactifs en Java
Animation interactive de solides de Platon.
Patrons en papiers de solides de Platon
Système de jouets éducatifs à base de blocs magnétiques sur les solides de Platon

Solides géométriques
Les polyèdres
Les solides de Platon
Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre
Les solides d'Archimède
Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre
Les solides de Kepler-Poinsot
Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre
Les solides de Catalan
Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre
Les solides de Johnson
Les solides de révolution
Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution

Portail de la géométrie

Ce document provient de « Solide de Platon ».

Catégorie : Polyèdre

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Solide platonicien de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Dé à dix faces — Un dé à dix faces (décaèdre) est une variante de dé, comportant dix faces. Les dés à dix faces sont principalement utilisés dans les jeux de rôle et des jeux de figurines (où ils sont souvent désignés par « D10 ») pour obtenir des… … Wikipédia en Français
1D10 — Dé à dix faces Un dé à dix faces, indiquant « 5 » comme résultat … Wikipédia en Français
D-10 — Dé à dix faces Un dé à dix faces, indiquant « 5 » comme résultat … Wikipédia en Français
D 10 — Dé à dix faces Un dé à dix faces, indiquant « 5 » comme résultat … Wikipédia en Français
De a dix faces — Dé à dix faces Un dé à dix faces, indiquant « 5 » comme résultat … Wikipédia en Français
Dé — Pour les articles homonymes, voir Dé (homonymie) et D6. Deux dés à jouer ordinaires. Un dé est un objet, généralement de petite taille et de forme cubique, qui permet de tirer aléatoirement un … Wikipédia en Français
Dé À Dix Faces — Un dé à dix faces, indiquant « 5 » comme résultat … Wikipédia en Français
Dé à 10 faces — Dé à dix faces Un dé à dix faces, indiquant « 5 » comme résultat … Wikipédia en Français
Dé à six faces — Dé Pour les articles homonymes, voir Dé (homonymie) et D6. Deux dés à jouer ordinaires. Un dé est un objet, généralement de petite taille et de forme … Wikipédia en Français
Dés — Dé Pour les articles homonymes, voir Dé (homonymie) et D6. Deux dés à jouer ordinaires. Un dé est un objet, généralement de petite taille et de forme … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Solide platonicien

Solide de Platon

Sommaire

Histoire

Propriétés combinatoires