Polyèdre dual
- Polyèdre dual
-
Dual d'un polyèdre
En géométrie, il existe plusieurs façons (géométrique, combinatoire) de mettre les polyèdres en dualité. Dans chaque cas, à tout polyèdre est associé un polyèdre appelé dual du premier, de telle sorte que
- le dual du polyèdre dual est le polyèdre initial,
- les faces de l'un sont en correspondance avec les sommets de l'autre, en respectant les propriétés d'adjacence.
L'exemple le plus simple de dualité s'obtient pour les polyèdres réguliers, en reliant les centres de faces adjacentes. Plus généralement, on définit une dualité en considérant l'opération de conjugaison par rapport à la sphère circonscrite.
On peut se passer de support géométrique et définir une notion de dualité en termes purement combinatoires, qui s'étend d'ailleurs aux polyèdres et polytopes abstraits.

Le tétraèdre est son propre dual
Le cube donne l'octaèdre, le dodécaèdre l'icosaèdre et le tétraèdre est son propre dual.
Le petit dodécaèdre étoilé est le dual du grand dodécaèdre, et le grand dodécaèdre étoilé celui du grand icosaèdre.
Les duaux des solides archimédiens sont les solides de Catalan.
Les duaux des prismes sont des diamants (ou bipyramides), ceux des antiprismes des antidiamants.
| géode par triangulation |
 |
géode en nid d'abeille |
 |
Dualité des solides de Platon
 |
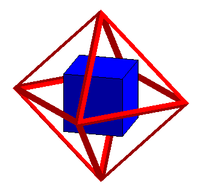 |
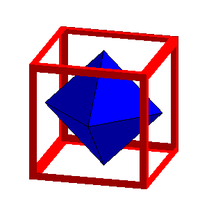
| Le dual du cube est l'octaèdre |
Le dual de l'octaèdre est le cube |
 |
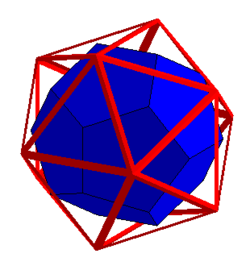 |
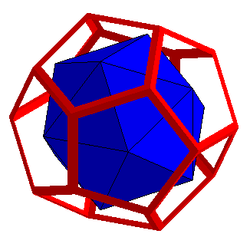
| Le dual du dodécaèdre est l'icosaèdre |
Le dual de l'icosaèdre est le dodécaèdre |
Voir aussi
Liens externes
 Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Polyèdre dual de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Polyedre — Polyèdre Un polyèdre particulier en dimension 3 : le dodécaèdre Un polyèdre est une forme géométrique à trois dimensions ayant des faces planes qui se rencontrent le long d arêtes droites. Le mot polyèdre provient du grec classique πολυεδρον … Wikipédia en Français
Dual D'un Polyèdre — En géométrie, il existe plusieurs façons (géométrique, combinatoire) de mettre les polyèdres en dualité. Dans chaque cas, à tout polyèdre est associé un polyèdre appelé dual du premier, de telle sorte que le dual du polyèdre dual est le polyèdre… … Wikipédia en Français
Dual d'un polyedre — Dual d un polyèdre En géométrie, il existe plusieurs façons (géométrique, combinatoire) de mettre les polyèdres en dualité. Dans chaque cas, à tout polyèdre est associé un polyèdre appelé dual du premier, de telle sorte que le dual du polyèdre… … Wikipédia en Français
Polyèdre — Un polyèdre est une forme géométrique à trois dimensions ayant des faces planes polygonales qui se rencontrent selon des segments de droite qu on appelle arêtes. Le mot « polyèdre »[1] provient du grec classique πολύεδρον (polyedron)… … Wikipédia en Français
Dual d'un polyèdre — Pour les articles homonymes, voir Dualité (mathématiques) et Dualité. En géométrie, il existe plusieurs façons (géométrique, combinatoire) de mettre les polyèdres en dualité. Dans chaque cas, à tout polyèdre est associé un polyèdre appelé dual du … Wikipédia en Français
Polyedre uniforme — Polyèdre uniforme Un polyèdre uniforme est un polyèdre qui a pour faces des polygones réguliers et peut passer d un sommet à l autre (i.e. il existe une isométrie qui applique un sommet quelconque sur un autre. Il en découle que tous les sommets… … Wikipédia en Français
Polyedre quasi-regulier — Polyèdre quasi régulier Sommaire 1 Définition 2 Les polyèdres quasi réguliers convexes 3 Exemples non convexes 4 Duaux quasi réguliers … Wikipédia en Français
dual — dual, duale [ dɥal; dyal ] adj. • 1948; du bas lat. dualis « deux » 1 ♦ Log., math. Se dit de propriétés qui sont par deux et qui présentent un caractère de réciprocité. Équation, expression duale, qui se déduit d une équation ou d une expression … Encyclopédie Universelle
Polyedre regulier — Polyèdre régulier Pour les articles homonymes, voir régulier. Un polyèdre est dit régulier s il est constitué de faces toutes identiques et régulières, et que tous ses sommets sont identiques. Ils sont au nombre de neuf, dont cinq sont convexes… … Wikipédia en Français
Polyèdre uniforme — Un polyèdre uniforme (en) est un polyèdre qui a pour faces des polygones réguliers et tel qu il existe une isométrie qui applique un sommet quelconque sur un autre. Il en découle que tous les sommets sont congruents, et que le polyèdre… … Wikipédia en Français