- Angle Solide
-
Angle solide
 L'angle solide est le rapport entre la surface (en rose) de la projection d'un objet sur une sphère et le carré du rayon de celle-ci. Ici, l'objet dont est mesuré l'angle solide est une surface quadrilatère (en bleu).
L'angle solide est le rapport entre la surface (en rose) de la projection d'un objet sur une sphère et le carré du rayon de celle-ci. Ici, l'objet dont est mesuré l'angle solide est une surface quadrilatère (en bleu).
En mathématiques, en géométrie et en physique, un angle solide est l'analogue tridimensionnel de l'angle plan ou bidimensionnel.
L'angle plan étant défini, dans l'espace bidimensionnel, comme le rapport de la longueur de l'arc sur le rayon d'un cercle, l'angle solide, dans l'espace tridimensionnel, est défini de façon analogue comme le rapport de la surface d'une partie d'une sphère sur le rayon au carré. Son unité est le stéradian noté sr.
On le note souvent Ω (oméga majuscule). Il mesure la surface sur laquelle un objet se projette radialement sur une sphère de rayon unité.
Sommaire
Calcul
Formule usuelle
Pour calculer l'angle solide sous lequel on voit un objet à partir d'un point donné, on projette l'objet sur une sphère de rayon R centrée en ce point.
Si la surface que cette projection fait sur la sphère est S, l'angle solide sous lequel l'observateur voit l'objet est, par définition :
La notion d'angle solide intervient en particulier dans la définition de la luminosité et de ses grandeurs dérivées. En général, ces grandeurs sont associées à des corps sources ou récepteurs dont les positions spatiales sont exprimées en coordonnées curvilignes (par exemple, en coordonnées sphériques : position des étoiles, satellites, capteurs au sol, etc.). On peut dès lors définir l'angle solide dans ce type de coordonnées.
Angle solide en coordonnées sphériques
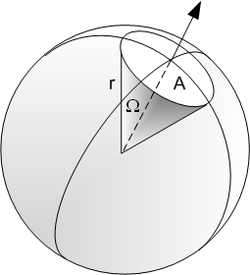
Pour une sphère de rayon r, l'angle solide est défini pour un élément de surface élémentaire dS, c'est-à-dire engendré par des variations angulaires infinitésimales des zénith θ et azimut φ (la surface élémentaire est assimilée à un plan) :
D'où :
Par intégration dans les domaines angulaires des coordonnées sphériques et en notant θ' et φ' les variables d'intégration :
Ceci définit un cône d'angle Ω = 2α et de base A.
Coin d'un tétraèdre
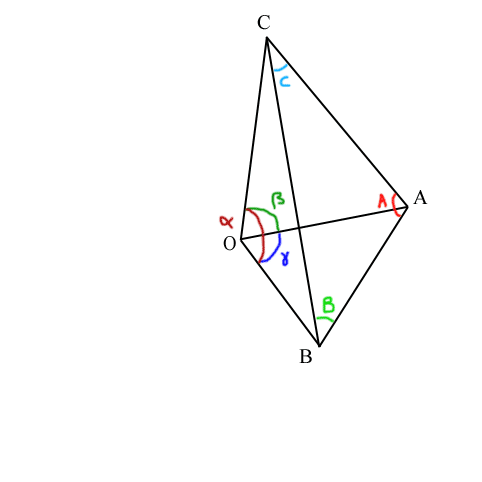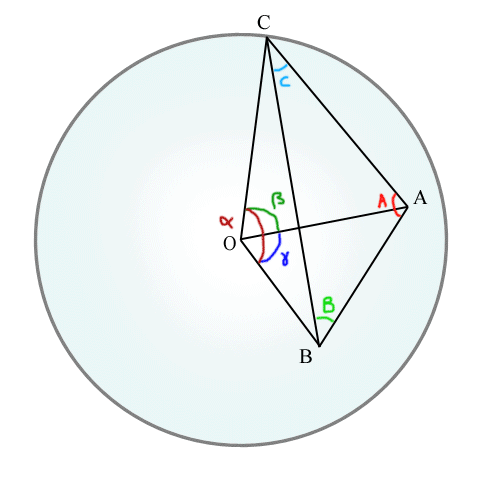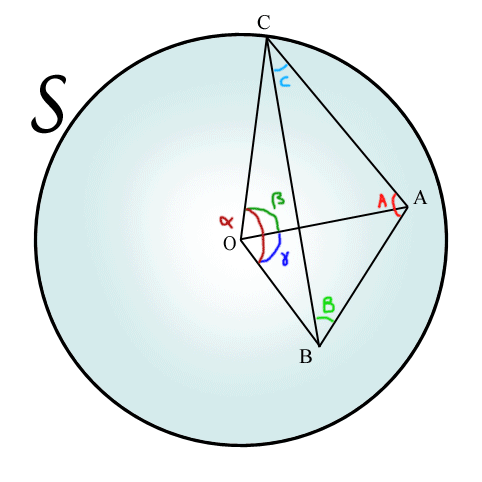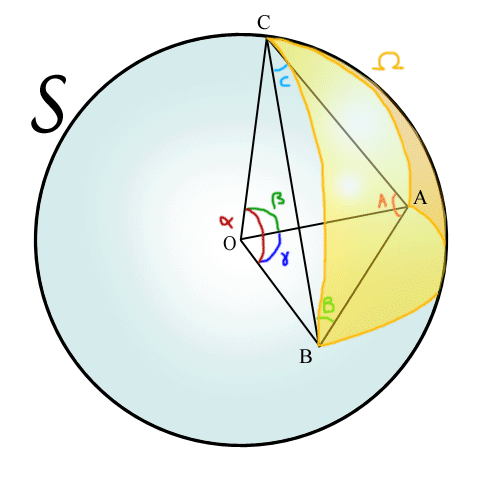 Le coin d'un tétraèdre, formé des angles α, β et γ, projette sur une sphère S la face opposée, donnant ainsi un triangle "gonflé" d'aire Ω aux angles arrondis A, B et C.
Le coin d'un tétraèdre, formé des angles α, β et γ, projette sur une sphère S la face opposée, donnant ainsi un triangle "gonflé" d'aire Ω aux angles arrondis A, B et C.
L'angle solide formé par trois angles α, β, γ (sommet d'un tétraèdre) vaut :
Ω = A + B + C − π
où A, B et C valent respectivement :
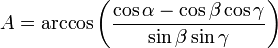
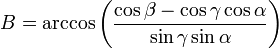
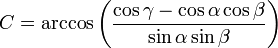
avec
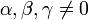 , et la somme de deux angles supérieure ou égale au troisième (sinon le coin est inconstructible).
, et la somme de deux angles supérieure ou égale au troisième (sinon le coin est inconstructible).Cas particuliers :
-
- Si jamais l'un des trois angles du tétraèdre α, β ou γ devient nul, alors les deux autres se superposent et deviennent égaux : l'angle solide Ω s'aplatit et devient alors nul.
- Si
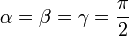 (tétraèdre à coin droit), alors
(tétraèdre à coin droit), alors 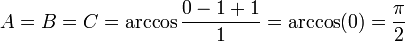 , donc
, donc 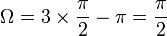 , soit le huitième d'une sphère.
, soit le huitième d'une sphère. - Si α + β + γ = 2π (tétraèdre plat), alors A = B = C = arccos( − 1) = π (angle sphérique plat : équateur) et Ω = 2π (demi sphère).
Quelques exemples
 Calotte sphérique dont le diamètre apparent est 2θ sr
Calotte sphérique dont le diamètre apparent est 2θ sr
- En reprenant la définition de l'angle solide en coordonnées sphériques, les angles θ = π/3, θ = π/2 et θ = 2π/3 délimitent un découpage de la sphère en quatre surfaces égales de π stéradians. Ainsi, l'espace complet est vu sous un angle solide de 4π sr.
- Un hémisphère correspond donc à un angle solide de 2π sr.
- Un trièdre, formé par deux murs perpendiculaires et le sol, décrit un angle solide de π/2 sr, soit un huitième de sphère.
- Entre la latitude de San Diego, en Californie, dans l'hémisphère Nord et celle de Sydney, en Australie, dans l'hémisphère Sud, il y a la moitié de la surface terrestre, soit un angle solide de 2π sr.
- Entre le cercle polaire et le tropique du Cancer, dans l'hémisphère Nord, il y a le quart de la surface terrestre, soit un angle solide de π sr.
- Les angles solides sous lesquels on voit une pièce d'un centime d'euro à 1,80 m de distance, la Lune et le Soleil, sont très proches : ≈6.10−5 sr (voir à ce sujet les éclipses solaires).
- Un « carré de ciel » de 0,923… radians de côté se voit sous un angle solide d'un stéradian.
Voir aussi
Articles connexes
Liens externes
- Portail de la géométrie
- Portail de la physique
Catégories : Angle | Grandeur physique
Wikimedia Foundation. 2010.

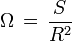
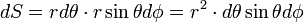
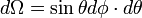
![\Omega = \int_0^{2\pi} d\phi' \int_0^{\alpha} \sin\theta' \ d\theta' \ = 2\pi\int_0^{\alpha} \sin \theta' \ d \theta' = 2\pi\left[ -\cos \theta' \right]_0^{\alpha} \ = 2\pi\left(1 -\cos \alpha \right)](/pictures/frwiki/51/3afa5bb29a6643be8e7fa48162029dd0.png)