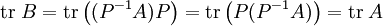Matrice Semblable

Matrice semblable

Article détaillé : réduction d'endomorphisme.

En mathématiques, deux matrices carrées A et B sont dites semblables s'il existe une matrice inversible P telle que :

A = P B P - 1

Il s'agit d'une relation d'équivalence.

Deux matrices sont semblables si et seulement si elles constituent deux matrices représentatives du même endomorphisme dans deux bases (éventuellement) différentes. Il ne faut pas confondre la notion de matrices semblables avec celle de matrices équivalentes. En revanche, si deux matrices sont semblables, alors elles sont équivalentes. Un moyen de déterminer si deux matrices sont semblables est de les réduire, c'est-à-dire de les ramener à une forme type : diagonale, forme réduite de Jordan…

Exemple

Les matrices suivantes sont semblables :

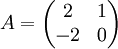
$A = \begin{pmatrix} 2 & 1 \\ -2 & 0 \end{pmatrix}$

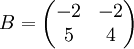$B = \begin{pmatrix} -2 & -2 \\ 5 & 4 \end{pmatrix}$ .

En effet, en posant :

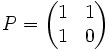$P = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}$ ,

on obtient : 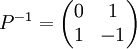$P^{-1} = \begin{pmatrix} 0 & 1 \\ 1 & -1 \end{pmatrix}$ ,

et on vérifie aisément que :

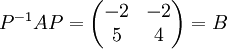$P^{-1} A P = \begin{pmatrix} -2 & -2 \\ 5 & 4 \end{pmatrix} = B$ .

Invariants de similitude

Les applications de l'espace des matrices carrées dont le résultat est identique pour une matrice et une matrice qui lui est semblable sont appelés invariants de similitude. En particulier, la trace d'une matrice est un invariant de similitude. Avec les notations précédentes :

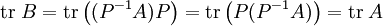
$\mathrm{tr}\; B = \mathrm{tr} \left( (P^{-1}A)P \right) = \mathrm{tr} \left( P (P^{-1}A) \right) = \mathrm{tr}\; A$

De même, le rang, le déterminant, les valeurs propres, le polynôme caractéristique et le polynôme minimal sont des invariants de similitudes.

Voir aussi

Articles en rapport avec les matrices
Par forme	carrée • triangulaire • diagonale • tridiagonale • élémentaire • échelonnée • creuse • aléatoire • circulante • de Hankel • de Toeplitz • de Vandermonde
Transformée	transposée • adjointe • inverse • Comatrice
En relation	équivalente • semblable • congruente
Par propriété	inversible • diagonalisable • trigonalisable • symétrique • antisymétrique • hermitienne • normale • orthogonale • unitaire • symplectique • de Hadamard • définie positive • à diagonale dominante • nilpotente
Par famille	identité • de De Casteljau • de Cartan • de Hilbert • de Mueller • de Pauli • de Dirac
Particulière	CKM
Associée	de permutation • de passage • compagnon • de Sylvester • d'adjacence • laplacienne • hessienne • jacobienne • génératrice • de contrôle • de corrélation • de Gram • de variance-covariance • d'inertie • de Jones • des gains • stochastique
Résultats	décompositions : LU • QR • polaire • valeurs singulières Trigonalisation • Réduction de Jordan • facteurs invariants
Voir aussi	Théorie des matrices • Algèbre linéaire

Matrices équivalentes

Portail des mathématiques

Ce document provient de « Matrice semblable ».

Catégorie : Matrice

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice Semblable de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Matrice semblable — Article détaillé : réduction d endomorphisme. En mathématiques, deux matrices carrées A et B sont dites semblables s il existe une matrice inversible P telle que : A = PBP − 1. Il s agit d une relation d équivalence. Deux matrices sont… … Wikipédia en Français
Matrice Nilpotente — Une matrice nilpotente est une matrice dont il existe une puissance égale à la matrice nulle. Elle correspond à la notion d endomorphisme nilpotent. Cette notion joue un rôle important dans le monde des matrices. En effet, pour un maniement plus… … Wikipédia en Français
Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice diagonalisable — ● Matrice diagonalisable matrice carrée qui admet une matrice semblable diagonale … Encyclopédie Universelle
Matrice diagonalisable — Exemple de matrice diagonalisable sur le corps des complexes mais pas sur celui des réels, son polynôme caractéristique étant X2 + 1. En mathématiques, une matrice diagonalisable est une matrice carrée semblable à une matrice diagonale. Cette p … Wikipédia en Français
Matrice (mathématiques) — Pour les articles homonymes, voir Matrice. En mathématiques, les matrices sont des tableaux de nombres qui servent à interpréter en termes calculatoires et donc opérationnels les résultats … Wikipédia en Français
Matrice nilpotente — Une matrice nilpotente est une matrice dont il existe une puissance égale à la matrice nulle. Elle correspond à la notion d endomorphisme nilpotent sur un espace vectoriel de dimension finie. Cette notion facilite souvent le calcul matriciel. En… … Wikipédia en Français
Matrice Diagonale — En algèbre linéaire, une matrice diagonale est une matrice carrée dont les coefficients en dehors de la diagonale principale sont nuls. Les coefficients de la diagonale peuvent être ou ne pas être nuls. Ainsi, la matrice D = (di,j) est diagonale… … Wikipédia en Français

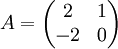
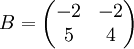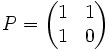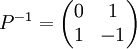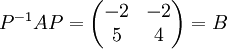Dictionnaires et Encyclopédies sur 'Academic'

Matrice Semblable