Matrice equivalente
- Matrice equivalente
-
Matrice équivalente
En mathématiques, deux matrices de même taille (m,n), A et B sont dites équivalentes si et seulement s'il existe deux matrices inversibles P et Q (respectivement de tailles (n,n) et (m,m)) telles que A = QBP − 1
Il s'agit d'une relation d'équivalence sur chaque ensemble de matrices d'une taille donnée.
Deux matrices A et B sont équivalentes si et seulement si elles peuvent représenter la même application linéaire 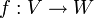 par rapport à deux couples (un pour A et un pour B) de bases (une base de V et une base de W) bien choisis. On pourra alors trouver des matrices P et Q qui établissent l'équivalence de A et B, en prenant P égale à la matrice de passage de la base de V utilisée pour A à la base de V utilisée pour B, et Q égale à la matrice de passage de la base de W utilisée pour A à la base de W utilisée pour B. C'est pour accommoder ces choix que c'est l'inverse de P qui figure dans la définition ci-dessus.
par rapport à deux couples (un pour A et un pour B) de bases (une base de V et une base de W) bien choisis. On pourra alors trouver des matrices P et Q qui établissent l'équivalence de A et B, en prenant P égale à la matrice de passage de la base de V utilisée pour A à la base de V utilisée pour B, et Q égale à la matrice de passage de la base de W utilisée pour A à la base de W utilisée pour B. C'est pour accommoder ces choix que c'est l'inverse de P qui figure dans la définition ci-dessus.
Deux matrices sont équivalentes si et seulement si elles ont même rang, qui est la plus petite dimension r telle que f puisse s'écrire comme la composée 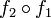 d'une application linéaire
d'une application linéaire 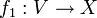 et d'une application linéaire
et d'une application linéaire 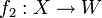 avec X un espace de dimension r.
avec X un espace de dimension r.
Il ne faut pas confondre la notion de matrices équivalentes avec celle de matrices semblables. Deux matrices nécessairement carrées sont semblables si elles peuvent représenter la même application linéaire 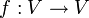 par rapport à deux bases de V bien choisies; la différence avec la notion d'équivalence est qu'ici on n'a pas le droit de choisir la base à l'arrivée independamment de la base au départ. Ainsi, tandis que deux matrices semblables sont forcément équivalentes, la réciproque est loin d'être vraie. En effet, deux matrices carrées dont les polynômes caractéristiques sont distincts ne peuvent pas être semblables, mais elles seront équivalentes dès qu'elles ont le même rang (par exemple si elles sont inversibles toutes les deux).
par rapport à deux bases de V bien choisies; la différence avec la notion d'équivalence est qu'ici on n'a pas le droit de choisir la base à l'arrivée independamment de la base au départ. Ainsi, tandis que deux matrices semblables sont forcément équivalentes, la réciproque est loin d'être vraie. En effet, deux matrices carrées dont les polynômes caractéristiques sont distincts ne peuvent pas être semblables, mais elles seront équivalentes dès qu'elles ont le même rang (par exemple si elles sont inversibles toutes les deux).
Voir aussi
|
Articles en rapport avec les matrices |
| Par forme |
|
| Transformée |
|
| En relation |
|
| Par propriété |
|
| Par famille |
|
| Particulière |
|
| Associée |
|
| Résultats |
|
| Voir aussi |
|
 Portail des mathématiques
Portail des mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Matrice equivalente de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Matrice Équivalente — En mathématiques, deux matrices de même taille (m,n), A et B sont dites équivalentes si et seulement s il existe deux matrices inversibles P et Q (respectivement de tailles (n,n) et (m,m)) telles que A = QBP − 1 Il s agit d une relation d… … Wikipédia en Français
Matrice équivalente — En mathématiques, deux matrices de même taille (m,n), A et B sont dites équivalentes si et seulement s il existe deux matrices inversibles P et Q (respectivement de tailles (n,n) et (m,m)) telles que A = QBP − 1 Il s agit d une relation d… … Wikipédia en Français
matrice équivalente — ekvivalentinė matrica statusas T sritis fizika atitikmenys: angl. equivalent matrix vok. äquivalente Matrix, f rus. эквивалентная матрица, f pranc. matrice équivalente, f … Fizikos terminų žodynas
Matrice (mathématiques) — Pour les articles homonymes, voir Matrice. En mathématiques, les matrices sont des tableaux de nombres qui servent à interpréter en termes calculatoires et donc opérationnels les résultats … Wikipédia en Français
Matrice Inversible — En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d ordre n est dite inversible ou régulière ou encore non singulière, s il existe une matrice B d ordre n telle que AB = BA = In, ( AB = In suffit d aprés le… … Wikipédia en Français
Matrice inverse — Matrice inversible En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d ordre n est dite inversible ou régulière ou encore non singulière, s il existe une matrice B d ordre n telle que AB = BA = In, ( AB = In… … Wikipédia en Français
Matrice non singulière — Matrice inversible En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d ordre n est dite inversible ou régulière ou encore non singulière, s il existe une matrice B d ordre n telle que AB = BA = In, ( AB = In… … Wikipédia en Français
Matrice régulière — Matrice inversible En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d ordre n est dite inversible ou régulière ou encore non singulière, s il existe une matrice B d ordre n telle que AB = BA = In, ( AB = In… … Wikipédia en Français
Matrice Diagonale — En algèbre linéaire, une matrice diagonale est une matrice carrée dont les coefficients en dehors de la diagonale principale sont nuls. Les coefficients de la diagonale peuvent être ou ne pas être nuls. Ainsi, la matrice D = (di,j) est diagonale… … Wikipédia en Français
Matrice scalaire — Matrice diagonale En algèbre linéaire, une matrice diagonale est une matrice carrée dont les coefficients en dehors de la diagonale principale sont nuls. Les coefficients de la diagonale peuvent être ou ne pas être nuls. Ainsi, la matrice D = (di … Wikipédia en Français
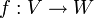 par rapport à deux couples (un pour A et un pour B) de bases (une base de V et une base de W) bien choisis. On pourra alors trouver des matrices P et Q qui établissent l'équivalence de A et B, en prenant P égale à la matrice de passage de la base de V utilisée pour A à la base de V utilisée pour B, et Q égale à la matrice de passage de la base de W utilisée pour A à la base de W utilisée pour B. C'est pour accommoder ces choix que c'est l'inverse de P qui figure dans la définition ci-dessus.
par rapport à deux couples (un pour A et un pour B) de bases (une base de V et une base de W) bien choisis. On pourra alors trouver des matrices P et Q qui établissent l'équivalence de A et B, en prenant P égale à la matrice de passage de la base de V utilisée pour A à la base de V utilisée pour B, et Q égale à la matrice de passage de la base de W utilisée pour A à la base de W utilisée pour B. C'est pour accommoder ces choix que c'est l'inverse de P qui figure dans la définition ci-dessus.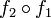 d'une application linéaire
d'une application linéaire 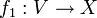 et d'une application linéaire
et d'une application linéaire 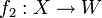 avec X un espace de dimension r.
avec X un espace de dimension r.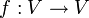 par rapport à deux bases de V bien choisies; la différence avec la notion d'équivalence est qu'ici on n'a pas le droit de choisir la base à l'arrivée independamment de la base au départ. Ainsi, tandis que deux matrices semblables sont forcément équivalentes, la réciproque est loin d'être vraie. En effet, deux matrices carrées dont les polynômes caractéristiques sont distincts ne peuvent pas être semblables, mais elles seront équivalentes dès qu'elles ont le même rang (par exemple si elles sont inversibles toutes les deux).
par rapport à deux bases de V bien choisies; la différence avec la notion d'équivalence est qu'ici on n'a pas le droit de choisir la base à l'arrivée independamment de la base au départ. Ainsi, tandis que deux matrices semblables sont forcément équivalentes, la réciproque est loin d'être vraie. En effet, deux matrices carrées dont les polynômes caractéristiques sont distincts ne peuvent pas être semblables, mais elles seront équivalentes dès qu'elles ont le même rang (par exemple si elles sont inversibles toutes les deux).