Icosaédre

Icosaédre

Icosaèdre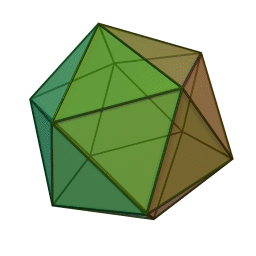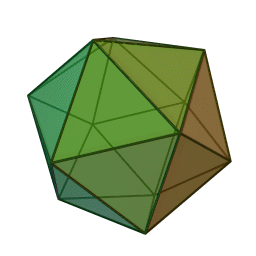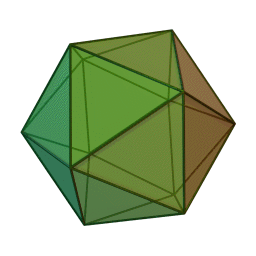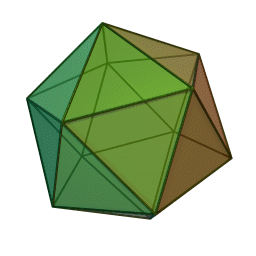

Icosaèdre
Icosaèdre
Type Polyèdre régulier
Faces Triangle
Éléments :
 · Faces
 · Arêtes
 · Sommets
 · Caractéristique		  
20
30
12
2
Faces par sommet 5
Sommets par face 3
Isométries A5xC2
Dual Dodécaèdre
Propriétés Deltaèdre régulier et convexe

En mathématiques, et plus précisément en géométrie, un icosaèdre est un solide de dimension trois, de la famille des polyèdres, c'est-à-dire que sa surface est composée d'un nombre fini de polygones et qu'il se décrit à l'aide de ses sommets ou de ses arêtes ou encore de ses différentes faces. Plus exactement, un icosaèdre est un polyèdre contenant exactement 20 faces. Le préfixe icosa-, d'origine grecque, fait référence au nombre de faces.

Il existe un icosaèdre régulier convexe. Le polyèdre est dit régulier si toutes les arêtes possèdent la même longueur et si tous les angles entre deux arêtes partageant un sommet et une même face sont égaux. Si tout segment dont les extrémités sont à l'intérieur du polyèdre est intégralement à l'intérieur du polyèdre, on parle de convexité. Il existe 5 polyèdres à la fois réguliers et convexes, ils sont appelés solides de Platon, en l'honneur du philosophe grec Platon.

Le groupe des rotations de l'icosaèdre est celui formé par les rotations de l'espace qui laissent invariant la position globale de l'icosaèdre, tout en permutant certaines faces. Il comporte 60 éléments et est une copie du groupe alterné de degré 5.

Un autre solide de Platon partage avec l'icosaèdre le même groupe de rotations, le dodécaèdre. On obtient un dodécaèdre en considérant le solide dont les sommets sont les centres des faces d'un icosaèdre. Réciproquement, on obtient un icosaèdre en considérant le solide ayant pour sommets les centres des faces d'un dodécaèdre. On dit que les solides de Platon icosaèdre et dodécaèdre sont duaux.

Sommaire

Géométrie de l'icosaèdre régulier convexe

Construction manuelle d'un icosaèdre

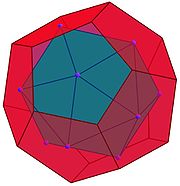
Si le bol inférieur est bleu et celui supérieur rouge, on obtient la figure illustrée ici.
Il existe de nombreux patrons de l'icosaèdre régulier, celui-ci est un exemple.

Un icosaèdre se construit à l'aide de 20 triangles équilatéraux de même dimension. On commence par assembler 5 des triangles par leurs arêtes de telle manière qu'ils forment un bol avec une pointe en bas. Ainsi la base du solide est un sommet partagé par les 5 triangles et le bord est composé de 5 segments, tous de même longueur, formant un pentagone régulier. Sur chacun des 5 segments formant la surface du bol, on colle un nouveau triangle de manière à ce que le côté supérieur de chaque triangle du bol soit aussi le côté inférieur d'un des 5 triangles ajoutés. On redresse ensuite les 5 triangles supérieurs de manière à ce que leurs faces soient verticales. On obtient alors un bol plus vaste, composé de 10 triangles, et dont la partie supérieure est formée de 5 dents .

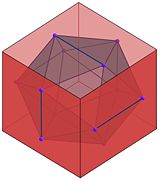
On construit une deuxième forme identique à la première. On a alors utilisé l'intégralité des 20 triangles. La deuxième forme s'emboite exactement dans le première, formant un polyèdre régulier. Il est illustré sur la figure de droite, le bol inférieur est bleu. On remarque sa calotte inférieure, puis les 5 dents, dont 3 sont face à un observateur et 2 derrière. Le bol supérieur, en rouge sur la figure possède la même géométrie. Pour les emboiter, il suffit de placer la calotte en haut et 2 dents en face de l'observateur.

On peut encore construire l'icosaèdre à l'aide du patron illustré sur la figure de droite. L'icosaèdre s'obtient en collant le côté libre du triangle jaune en haut à gauche sur le côté libre du triangle orange, en bas à droite. Les 5 triangles rouges, connexes aux triangles orange sont alors approchés pour que leurs sommets libres se confondent en un seul point. La même opération, effectuée sur les 5 triangles rouges, connexes aux triangles jaunes, termine la construction de l'icosaèdre. Le patron présenté ici est un exemple, il en existe bien d'autres. On en trouve 43.380[1].

Propriétés

Un icosaèdre comporte 20 faces. Il possède 12 sommets, 1 en bas, 5 à la base inférieure des dents décrites dans la première construction et autant pour le bol supérieur. Il possède 30 arêtes, chacun des 12 sommets possède 5 arêtes, soit 60, mais comme une arête contient 2 sommets, il faut diviser 60 par 2 pour obtenir le bon résultat.

Sommets, arêtes et faces —  Un icosaèdre régulier convexe contient 12 sommets, 30 arêtes et 20 faces.

Il existe une sphère de centre celui de l'icosaèdre, contenant tous les sommets du polyèdre.
Le cube circonscrit de l'icosaèdre contient tous les sommets du polyèdre.

Les plus grands segments inclus dans le polyèdres ont tous pour extrémités deux sommets du polyèdre. Il en existe 6 et l'intersection de ces 6 segments est un point, appelé centre du polyèdre. Ce point est aussi le centre de gravité du solide. Il existe 10 segments d'extrémités deux points de la surface du polyèdre, passant par le centre et de longueur minimale. Les extrémités sont les centres de deux faces opposées, elles sont parallèles entre elles. Ces remarques géométriques permettent de qualifier la sphère circonscrite et celle inscrite du solide. La sphère circonscrite est celle de plus petit rayon dont l'intérieur contient l'intérieur du polyèdre. Celle définition généralise celle de cercle circonscrit. On peut de même parler de sphère inscrite pour désigner celle de plus grand rayon dont l'intérieur est inclus dans l'intérieur du solide, généralisant ainsi la définition de cercle inscrit.

Sphère circonscrite et inscrite —  La plus petite sphère dont l'intérieur contient l'intérieur de l'icosaèdre est de même centre que le solide, elle contient tous les sommets du polyèdre. La plus grande sphère contenue dans l'icosaèdre est aussi de même centre que le solide, elle contient le centre de chaque face du polyèdre.

Une analyse rapide pourrait laisser penser qu'il existe un cercle contenant 6 des sommets du polyèdre, il n'en est rien. Un cercle contient un maximum de 4 sommets. Cette erreur est, par exemple, commise par Albrecht Dürer[2], un peintre du XVIe siècle. En revanche, Dürer ne commet pas d'erreur quand il affirme que :

Cube circonscrit —  Le plus petit cube contenant l'icosaèdre est de même centre que le solide, sa surface contient tous les sommets du polyèdre.

Cette propriété est illustrée sur la figure de droite. Chacune des faces du cube contient deux sommets et une arête du polyèdre. Le cube contient 6 faces, donc les 12 sommets.

La structure de ce polyèdre est régulière. Les arêtes possèdent toutes la même longueur, deux arêtes d'une même face et possédant un sommet commun forment toujours le même angle, égal à 60 degré ou encore à π/3, si la mesure de l'angle est le radian. Le nombre d'arêtes partageant un même sommet est une constante qui ne dépend pas du sommet choisi[3]. On parle de polyèdre régulier. Un segment ayant ses deux extrémités à l'intérieur du solide est intégralement à l'intérieur du solide, on dit que l'icosaèdre est convexe. Une autre manière de voir les choses est de remarquer qu'un élastique qui entoure le solide le touche en chaque point. Ces deux manières de voir sont équivalentes. Les polyèdres réguliers ne sont pas toujours convexes, un contre exemple est donné à la suite de l'article. Les polyèdres réguliers convexes sont appelés solide de Platon.

Solide de Platon —  Il existe un icosaèdre, c'est-à-dire un polyèdre à 20 faces, qui est à la fois régulier et convexe. On dit que ce volume est un solide de Platon.

Rotation et symétrie

Une rotation laisse globalement invariant l'icosaèdre, lorsque l'image du solide par la rotation occupe exactement la même position que celle initiale. Les sommets, les arêtes et les faces sont peut-être permutés, mais la position globale est inchangée.

Rotations de l'icosaèdre —  Il existe 60 rotations laissant globalement invariant l'icosaèdre : la rotation d'angle nul, 15 rotations d'un demi-tour, 20 rotations d'un tiers de tour et 24 rotations d'un angle multiple d'un cinquième de tour.

Rotation d'un demi-tour des sommets de l'icosaèdre

Dans le cas d'un solide de Platon, une rotation qui laisse globalement invariant l'icosaèdre possède un axe qui traverse nécessairement le centre du solide et qui passe, soit par un sommet, soit par le milieu d'une arête, soit par le milieu d'une face.

Étudions, dans un premier temps, les rotations dont l'axe contient le centre d'une arête. Pour comprendre leur nature, le plus simple est de regrouper les points dans des plans perpendiculaires à l'axe de la rotation. Ce regroupement est effectué sur la figure de droite. Il met en évidence cinq ensembles. Les deux extrêmes, en bleu, sont composés de deux points formant les arrêtes qui délimitent le solide et qui croisent en leur milieu l'axe étudié. On trouve ensuite deux ensembles de deux points, illustré en rouge sur la figure, qui se trouvent sur deux droites perpendiculaires à la fois aux segments bleus et à l'axe de rotation. Enfin, au milieu du polyèdre, on trouve 4 points formant un rectangle. Ces 5 figures sont invariantes par une rotation d'un demi-tour. On en déduit l'existence d'une rotation d'un demi-tour pour chaque couple d'arêtes situées aux antipodes l'une de l'autre. Comme il existe 30 arêtes, on a 15 rotations d'un demi-tour. Aucune autre rotation autour de l'axe ne laisse invariant le solide, à l'exception de la rotation identité. En effet, les autres rotations ne laissent pas invariant un segment perpendiculaire à l'axe de rotation et non réduit à un point.

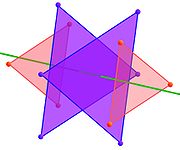
Rotation d'un tiers de tour des sommets de l'icosaèdre

Il existe deux autres axes de rotations, qui forment avec le premier, 3 axes dont les rotations d'un demi-tour laissent globalement invariant l'icosaèdre. Ces trois axes sont perpendiculaires entre eux, les rotations commutent entre elles.

La figure de gauche illustre le cas d'un axe passant par le centre du solide et qui traverse la surface du polyèdre par le centre de deux faces opposées. La même technique que celle utilisée précédemment regroupe cette fois ci les sommets en quatre ensembles. Par construction, les deux ensembles extrêmes sont des faces. Ce sont des triangles équilatéraux de même dimension et pivotés de demi-tour, l'un par rapport à l'autre. Les deux ensembles centraux, en violet sur la figure, sont aussi des triangles équilatéraux, de dimensions plus grandes. Une rotation d'un demi-tour est nécessaire pour faire coïncider deux triangles situés l'un à côté de l'autre. L'axe étudié traverse chacun des 4 triangles en son centre, on en déduit qu'à l'exception de la rotation d'un angle nul, seul les rotations d'un tiers de tour, dans un sens ou dans un autre laissent les sommets invariants.

Rotations d'un multiple d'un cinquième de tour des sommets de l'icosaèdre

Il existe 2 rotations d'un tiers de tour par couple de faces. Le solide contient 20 faces, on en déduit qu'il existe 20 rotations de cette nature.

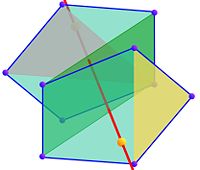
La figure en bas à droite du paragraphe illustre le cas d'un axe passant par le centre du solide et qui traverse la surface du polyèdre par deux sommets opposés. Les sommets sont encore regroupés en 4 ensembles. Les deux extrêmes sont composés d'un unique point, les deux ensembles les plus proches du centre forment chacun un pentagone régulier. Ils sont de même dimension et sont encore décalés d'un demi tour. Les seules rotations qui laissent globalement invariant un pentagone sont celles d'un angle multiple d'un cinquième de tour.

Il existe 4 rotations d'axes passant par deux sommets, laissant globalement invariant le solide, si l'on néglige la rotation d'angle nul. Il existe 12 sommets et 6 axes contenant deux sommets opposés, soit 24 rotations de cette nature.

Une fois déterminée les rotations, il devient simple de trouver les autres isométries, c'est-à-dire celles correspondant à des réflexions ou à une symétrie centrale. On les appelle parfois symétrie impropre, en opposition à symétrie propre qui ne désigne que les rotations. Une symétrie impropre est une isométrie qui n'est pas une rotation, ou encore dont le déterminant est égal à -1. La composée de deux symétries impropres est une rotation.

La première symétrie impropre à laquelle on peut penser est la symétrie centrale γ de centre celui du polyèdre. Les différentes illustrations précédentes montrent toutes qu'elle laisse globalement invariant le solide. Si σ est une symétrie impropre quelconque, sa composée avec γ est une rotation, notée ici ρ. L'isométrie γ est involutive, c'est-à-dire qu'appliquer deux fois γ revient à ne pas bouger le solide. On en déduit que σ est la composée d'une des rotations déjà explicitée avec γ. Si ρ1 et ρ2 sont deux rotations différentes, alors γ.ρ1 et γ.ρ2 sont deux symétries différentes. Pour s'en rendre compte, il suffit que composer ces deux symétries par γ, on obtient les deux rotations ρ1 et ρ2 car γ est involutive. Si les deux symétries étaient identiques, leurs composées le seraient aussi, comme ce n'est pas le cas, on en déduit qu'elles sont différentes. Il existe exactement 60 symétries impropres.

La composée d'une symétrie centrale par une rotation d'un angle non nul et dont l'axe contient le centre de symétrie est une réflexion. On en déduit que l'ensemble des symétries impropre est composée d'une symétrie centrale γ et de 59 réflexions.[4]

Symétries impropres de l'icosaèdre —  Il existe 60 symétries impropres laissant globalement invariant l'icosaèdre : la symétrie centrale de centre celui du solide et 59 réflexions, toutes ayant leur plan de symétrie contenant le centre du solide.

Figures remarquables de l'icosaèdre

Les polygones associés au nombre d'or sont présent dans l'icosaèdre.

Les symétries d'ordre 3 et 5 introduisent les figures géométriques planes associées à ces symétries.

Une symétrie plane d'ordre 3 a pour groupe de symétrie le triangle équilatéral (cf Réseau (géométrie)). Il est naturel d'en trouver la trace dans l'icosaèdre. Il est possible de construire de tels triangles avec les différents sommets du solide. Chaque axe passant par le centre de deux faces opposées traverse en leurs centres 4 triangles équilatéraux. Deux de ces triangles sont des faces. Les deux autres, représentés en violet sur la figure du paragraphe précédent, ont un coté en proportion d'extrême et moyenne raison par rapport à une arête du polyèdre. Ceci signifie que le coté d'un rectangle violet, divisé par la longueur d'une arête est égal au nombre d'or.

Pour chaque paire de faces, on trouve 2 petits triangles équilatéraux et 2 grands, soit un total de 12 petits triangles équilatéraux et autant de grands.

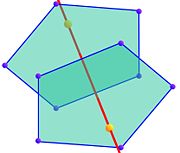
La présence du nombre d'or n'est guère surprenante, elle intervient dans l'expression d'une rotation d'ordre 5 et par conséquent dans les rapports de dimensions d'un pentagone. Parallèlement à chaque axe passant par deux sommets opposés, on trouve deux pentagones dont le plan est orthogonal à l'axe. Chaque sommet du pentagone est aussi un sommet de deux triangles d'or de géométries différentes. Un triangle est dit d'or quand il est isocèle et que le grand et le petit coté sont en proportion d'extrême et de moyenne raison. Il en existe deux types différents, ceux ayant deux grands cotés, en gris sur la figure de droite et ceux ayant deux petits cotés, en jaune. Chaque sommet d'un pentagone est le sommet adjacent à deux cotés égaux d'un triangle d'or de chaque type. La figure contient 2 pentagones, soit 10 sommets et 20 triangles d'or. Il existe 6 axes différents passant par deux sommets opposés, soit 120 triangles d'or.

On trouve aussi des rectangles d'or, c'est-à-dire des rectangles dont la longueur et la largeur ont un rapport égal au nombre d'or. On en trouve exactement 1 par coté du pentagone, le deuxième coté se situe alors sur l'autre pentagone. Un exemple est illustré en vert sur la figure de droite. Comme il existe 5 paires d'arêtes de cette nature pour chaque couple de pentagones, on trouve 30 rectangles d'or.

Polyèdre dual

Article détaillé : Polyèdre dual.
Le polyèdre dual d'un dodécaèdre est un icosaèdre.

A l'aide d'un polyèdre régulier, il est possible d'en construire un nouveau, de sommets les centres des faces du solide initial. Le dual d'un solide de Platon est encore un solide de Platon.

Dans le cas d'un icosaèdre, le dual possède 20 sommets et chaque face est un pentagone régulier car chaque sommet est partagé par 5 arêtes. Le polyèdre obtenu est un dodécaèdre régulier convexe, un solide composé de 12 faces pentagonales. Réciproquement, le dual d'un dodécaèdre, solide de Platon, est un polyèdre régulier convexe à 12 sommets. Comme chaque sommet du dodécaèdre est partagé par 3 arêtes, les faces de son dual sont des triangles équilatéraux. On reconnaît l'icosaèdre. Cette propriété est générale aux polyèdres, le dual du dual d'un polyèdre est une homothétie du solide initial.

Une symétrie qui laisse globalement invariant l'icosaèdre laisse aussi invariant l'ensemble des milieux de ses faces. On en déduit que toute symétrie de l'icosaèdre est aussi une symétrie du dodécaèdre. Réciproquement, le même raisonnement montre que toute symétrie du dodécaèdre est aussi une symétrie de l'icosaèdre. Les deux ensembles d'isométries, associés aux deux polyèdre duaux sont les mêmes. Ici, le terme de symétrie est utilisé au sens d'isométrie.

Grandeur caractéristique

Le tableau suivant présente les différentes grandeurs caractéristiques de l'icosaèdre régulier convexe[5] :

Dimensions d'un icosaèdre dont la longueur de l'arête est a
Angle diédral 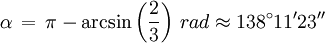\alpha \,=\, \pi-\arcsin\left(\frac 23\right)\, rad \approx 138^{\circ}11'23''
Rayon de la sphère circonscrite 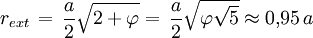r_{ext} \, = \, \frac{a}{2} \sqrt{2+\varphi} = \,\frac{a}{2} \sqrt{\varphi \sqrt 5} \approx 0{,}95 \, a
Rayon de la sphère inscrite 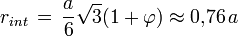r_{int} \, = \, \frac{a}{6} \sqrt{3}(1 + \varphi) \approx 0{,}76 \, a
Arête du cube circonscrit 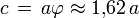c \, = \, a\varphi \approx 1{,}62 \, a
Hauteur de l'icosaèdre
(distance entre deux faces opposées)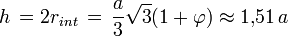		 h\, = 2 r_{int} \, = \, \frac{a}{3} \sqrt{3}(1 + \varphi) \approx 1{,}51 \, a
Volume 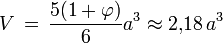V \, = \, \frac{5(1 + \varphi)}{6} a^3 \approx 2{,}18 \, a^3
Fraction de sphère circonscrite occupée 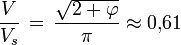\frac{V} {V_{s}}\, = \,\frac{\sqrt{2 + \varphi}}{\pi}\approx 0{,}61
Surface 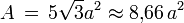A\, = \, 5 \sqrt{3} a^2 \approx 8{,}66 \, a^2
Quotient isopérimétrique 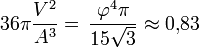36\pi \frac{V^2}{A^3} = \, \frac{\varphi^4 \pi}{15\sqrt 3} \approx 0{,}83

L'angle diédral est l'angle entre deux plans contenant chacun une face de l'icosaèdre. Les deux faces partagent un même sommet.

Fascination de l'icosaèdre

  • Dans certains jeux de rôle, le dé à 20 faces (abrégé d20) est utilisé pour déterminer le succès ou l'échec d'une action. Ce dé est un icosaèdre.
  • En biologie moléculaire, beaucoup de virus, comme le virus de l'Herpès, ont la forme d'un icosaèdre. Les structures virales sont formées de sous-unités protéiques identiques répétées, et la forme d'un icosaèdre est la forme la plus adaptée pour assembler ces sous-unités, car elle permet un espace maximal pour le génome viral. En effet, parmi les solides de Platon, l'icosaèdre optimise la place occupée dans la sphère circonscrite.[réf. nécessaire]
  • En remplaçant chaque face de l'icosaèdre par une résistance de 1 ohm, la mesure de la résistance entre deux coins opposés donne 0.5 ohms, et entre deux coins adjacents 11/30 ohms.

Structure mathématique d'un icosaèdre, solide de Platon

Construction par les coordonnées

Il existe un repère cartésien orthonormal permettant d'exprimer simplement les coordonnées des sommets de l'icosaèdre, si la longueur d'une arête est égale à 2.

La première partie de cet article présente plusieurs résultats mais aucune preuve. L'existence même d'un icosaèdre régulier convexe n'est pas démontrée. Une méthode simple consiste à déterminer des points, candidat à être les sommets d'un polyèdre régulier convexe. La démarche utilisée ici consiste à trouver un ensemble de points E possédant 4 propriétés qui sont vérifiées si ces points sont les sommets de l'icosaèdre :

  • L'ensemble E possède 12 sommets,
  • il existe une sphère contenant tous les points de E,
  • Le polyèdre P enveloppe convexe de E, possède des faces formant toutes des triangles équilatéraux et,
  • si l'on choisit astucieusement le repère, multiplier n'importe quelle coordonnée d'un sommet par -1 d'un point de E donne encore un point de E.

La dernière propriété est une conséquence de la stabilité de l'icosaèdre par trois rotations d'un demi-tour et d'axes perpendiculaires deux à deux. Pour obtenir des calculs simples, il est judicieux de fixer la longueur d'une arête à 2 et de positionner celle la plus à droite, parallèle à l'axe des y. On obtient les coordonnées suivantes :

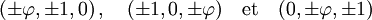
(\pm \varphi, \pm 1, 0)\,,\quad (\pm 1, 0, \pm\varphi)\quad \text{et}\quad (0,\pm\varphi, \pm 1)

Ici φ désigne le nombre d'or, égal à 1/2.(1 + √5). Une fois les coordonnées établies, on dispose d'une preuve de l'existence d'un icosaèdre régulier convexe à 12 sommets. On peut en effet montrer que P est un polyèdre régulier à 12 sommets. Il suffit de vérifier que pour tout sommet, il existe exactement 5 arêtes contenant ce sommet, qu'elles sont de mêmes longueurs et que ces 5 arêtes définissent bien 5 triangles équilatéraux.

Ces coordonnées permettent aussi de calculer les constantes caractéristiques de l'icosaèdre, décrites dans le paragraphe précédent.[6]

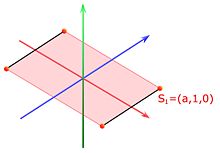
Détails des calculs

On cherche à construire l'ensemble E, de centre le vecteur nul et dont les arêtes sont de longueur 2. On choisit comme base orthonormale (e1, e2, e3), définie dans la boite déroulante précédente à la troisième proposition. Soit S1 un point de E tel que sa première coordonnée soit la plus grande possible, et soit (a, b, c) les coordonnées de S1.

  • Quitte à permuter e2 et e3, les coordonnées de S1 sont (a, 1, 0) et il existe trois autres points S2, S3 et S4 de E, de coordonnées (a, -1, 0), (-a, 1, 0) et (-a, -1, 0) :
Icosaèdre coordonnées 1.jpg

On sait qu'il est possible de multiplier chaque coordonnée d'un point de E par -1 sans quitter l'ensemble, on en déduit que les quatre points (a, ±b, ±c) sont dans E. Comme ces points sont les plus à droite de E, ils sont situés sur une même face. Aucune face ne contient 4 points, on en déduit que soit b soit c est nul. Quitte à permuter e2 et e3, on peut choisir c nul. L'arête à l'extrémité de l'axe de la rotation du groupe de symétrie, dirigée par e1 possède pour extrémité S1 de coordonnées (a, b, 0) et S2 de coordonnées (a, -b, 0). Une arête a pour longueur 2, ce qui montre que b est égal à 1.

Comme il est possible de multiplier par -1 n'importe quelle coordonnée d'un sommet pour obtenir les coordonnées d'un nouveau sommet, les deux points (-a, ±1, 0) sont aussi des sommets.

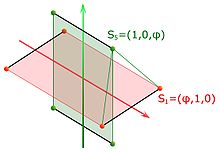
Icosaèdre coordonnées 2.jpg
  • Les 4 points supplémentaires S5 à S8 de coordonnées respectives (1, 0, a), (-1, 0, a), (1, 0, -a) et (-1, 0, a) sont dans E :

Les points S1 et S2 définissent une arête partagée par deux faces du polyèdre. Soit S5 le troisième sommet de la face se trouvant dans la zone des troisièmes coordonnées positives. Le point S5 est dans le plan situé à équidistance entre S1 et S2. On en déduit que la deuxième coordonnée de S5 est nulle. Soit (f, 0, g) ces coordonnées, on obtient comme précédemment 4 nouveaux sommets de coordonnées (±f, 0, ±g). Une fois connu f et g, il ne restera plus que 4 points à trouver.

Considérons le dernier sommet d'une face contenant l'arête d'extrémité (f, 0, g) et (a, 1, 0). Sa troisième coordonnée est strictement plus petite que celle de g. La multiplication des coordonnées par ±1 donne les sommets restants. On en déduit que les points S5 et S6, de troisième coordonnée égal à g sont les deux plus hauts du polyèdre. Ils forment une arête, ce qui montre que g est égal à 1. Le carré de la norme de S5 est égal à 1 + f 2. Il est encore égal au carré de la norme de S1, c'est-à-dire 1 + a2, car il existe une sphère de centre le vecteur nul, contenant tous les points de E. Comme a et f sont choisis positifs, a est égal à f. Ceci termine la démonstration de la proposition.

  • La valeur de a est égale au nombre d'or :
Icosaèdre coordonnées 3.jpg

La distance séparant S1 de S5 est égale à 2, ce qui donne l'équation suivante :

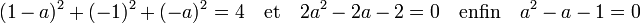
(1-a)^2 + (-1)^2 + (-a)^2 = 4 \quad\text{et}\quad 2a^2 -2a - 2 = 0 \quad\text{enfin}\quad a^2 - a - 1 = 0\;

L'équation précédente admet une unique solution positive. Par définition, cette valeur est égale au nombre d'or.

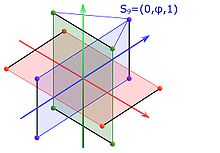
  • Les 4 points S9 à S12 de coordonnées respectives (0, φ, 1), (0, φ, -1), (0, -φ, 1), (0, -φ, -1) sont des 4 derniers points de E :

Considérons le point S9 de deuxième coordonnée positive et troisième sommet de la face contenant l'arête [S5, S6]. Un argument de symétrie déjà utilisé montre que sa première coordonnée est nulle. Un autre argument déjà utilisé montre que sa deuxième coordonnée est maximale dans les sommets du polyèdre, ce qui montre que sa troisième coordonnée est égale à 1. Comme S9 est sur la sphère dont le carré du rayon est égal à φ2 + 1, et que sa deuxième coordonnée est positive, elle est égale à φ.

Il suffit de multiplier par -1 les différentes coordonnées de S9 pour trouver les 3 autres.

 
Calcul des constantes caractéristiques de l'icosaèdre.

Pour être rigoureux, il est nécessaire de montrer que l'enveloppe convexe des points de E forme bien un polyèdre régulier. Le calcul direct est un peu fastidieux, le paragraphe suivant offre une preuve alternative. L'analyse des représentations d'un groupe de 60 éléments montre l'existence d'un solide de Platon à 12 sommets et contenant comme faces des triangles équilatéraux et que les 12 sommets sont situés sur une sphère. Il montre aussi l'existence de 3 rotations d'un demi-tour et d'axes orthogonaux deux à deux. Comme les 12 points de E correspondent à l'unique solution, à une rotation près, vérifiant ces propriétés si la longueur d'une arête est égale à 2, son enveloppe convexe est nécessairement un icosaèdre régulier.

Les calculs des coordonnées des sommets montrent, par homothétie de rapport a/2, si a est un réel strictement positif, que les coordonnées d'un icosaèdre régulier convexe sont, dans un repère bien choisi :

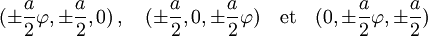
(\pm \frac a2\varphi, \pm \frac a2, 0)\,,\quad (\pm \frac a2, 0, \pm \frac a2\varphi)\quad \text{et}\quad (0,\pm \frac a2\varphi, \pm \frac a2)
  • Le rayon de la sphère circonscrite est égal à rext, avec :
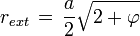
r_{ext} \, = \, \frac{a}{2} \sqrt{2+\varphi}

Les points de plus grandes normes de l'icosaèdre sont les sommets, le rayon rext est égal à la norme d'un sommet et :

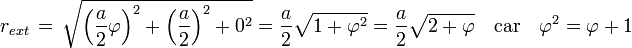
r_{ext} \, = \,\sqrt {\left(\frac a2\varphi\right)^2 + \left(\frac a2\right)^2 + 0^2} = \frac{a}{2}\sqrt{1+\varphi^2} = \frac{a}{2}\sqrt{2+\varphi}\quad\text{car}\quad \varphi^2 = \varphi + 1
  • Le rayon de la sphère inscrite est égal à rint, avec :
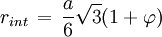
r_{int} \, = \, \frac{a}{6} \sqrt{3}(1 + \varphi)

Les points de plus petites normes de la surface de l'icosaèdre sont les milieux des faces. Le point M de coordonnées données par les calculs suivant est le milieu d'une face :

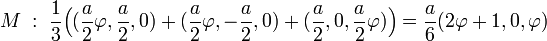
M \; :\; \frac 13 \Big((\frac a2\varphi, \frac a2, 0) + (\frac a2\varphi, -\frac a2, 0) + (\frac a2, 0 , \frac a2\varphi)\Big) = \frac a6(2\varphi +1, 0, \varphi)

Un calcul de la norme de M permet de finaliser la détermination :

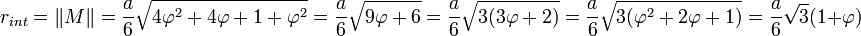
r_{int} = \|M\| = \frac a6\sqrt {4\varphi^2 + 4\varphi + 1 + \varphi^2} =\frac a6\sqrt {9\varphi + 6} = \frac a6\sqrt {3(3\varphi + 2)}= \frac a6\sqrt {3(\varphi^2 + 2\varphi + 1)}= \frac{a}{6} \sqrt{3}(1 + \varphi)
  • L'arête du cube circonscrit est égale à a.φ :

L'arête du cube circonscrit possède une longueur égale à la distance entre deux centres d'arêtes opposées de l'icosaèdre. Le point de coordonnées (a.φ/2, 0, 0) est le centre d'une arête. Le centre de l'arête opposée a pour coordonnées (-a.φ/2, 0, 0), ce qui permet d'en déduire le résultat.

  • La surface du polyèdre est égale à 5.√3.a2 :

Une face est un triangle équilatéral de côté a. Sa hauteur est donnée par l'application du théorème de Pythagore, on trouve √3.a/2. Sa surface est le produit de la moitié de la longueur d'un coté par la hauteur, on trouve √3.a2/4. La surface du polyèdre est composé de 20 faces, ce qui permet de trouver le résultat.

  • Le volume du polyèdre est égal à V, avec :
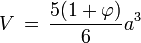
V \, = \, \frac{5(1 + \varphi)}{6} a^3

L'icosaèdre se décompose en 20 cônes de sommet le centre du solide et de base une face de surface Sf. On en déduit la formule, si d désigne la distance entre le centre du solide et celui d'une face :

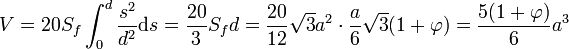
V = 20S_f\int_0^d \frac {s^2}{d^2}\text{d}s = \frac {20}3 S_f d = \frac {20}{12} \sqrt 3 a^2\cdot \frac{a}{6} \sqrt{3}(1 + \varphi) = \frac{5(1 + \varphi)}{6} a^3
  • Un icosaèdre occupe une fraction V/Vs du volume de la sphère circonscrite, avec :
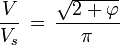
\frac{V} {V_{s}}\, = \,\frac{\sqrt{2 + \varphi}}{\pi}

Le rayon de la sphère circonscrite est égal à rext, une valeur déjà calculée. On en déduit le volume Vs de la sphère :

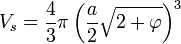
V_s = \frac 43 \pi \left(\frac{a}{2} \sqrt{2+\varphi}\right)^3

La connaissance du volume de l'icosaèdre permet de finir le calcul :

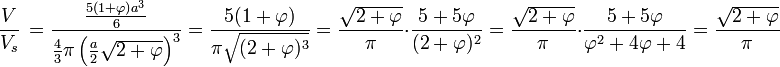
\frac{V} {V_{s}}\, = \frac {\frac{5(1 + \varphi)a^3}{6}}{\frac 43 \pi \left(\frac{a}{2} \sqrt{2+\varphi}\right)^3} = \frac {5(1 + \varphi)}{\pi\sqrt{(2+\varphi)^3}}= \frac{\sqrt{2 + \varphi}}{\pi}\cdot \frac {5 + 5\varphi}{(2+\varphi)^2}=\frac{\sqrt{2 + \varphi}}{\pi}\cdot \frac {5 + 5\varphi}{\varphi^2+ 4\varphi + 4}=\frac{\sqrt{2 + \varphi}}{\pi}
  • Quotient isopérimétrique :

Cette question est traitée dans l'article Isopérimétrie.

 

Groupe de symétrie

Article détaillé : Groupe de symétrie.

La loi de composition des isométries d'un espace euclidien de dimension 3 confère à l'ensemble de ces applications une structure de groupe. Les isométries laissant globalement invariant l'icosaèdre est un sous-groupe, d'ordre 120, dénommé groupe de symétrie de l'icosaèdre. Ce groupe contient lui-même un sous-groupe, composé des rotations, il est dénommé groupe de symétrie propre. Il contient 60 éléments et sa structure est connue. Elle est une copie d'un sous-groupe du groupe des permutations d'un ensemble de 5 éléments. Cette structure de 60 éléments est constitué par toutes les permutations qui s'obtiennent en combinant des permutations qui bougent 3 éléments et en laissent 2 stables, elle porte le nom de groupe alterné de degré 5. L'existence d'une telle structure permet d'étudier l'icosaèdre à l'aide d'une démarche usant de techniques radicalement différentes et issues de la théorie des groupes. La théorie des représentations d'un groupe fini nous indique que, en un certain sens, il n'existe qu'une manière d'incarner le groupe A5, en un ensemble de 60 rotations d'un espace euclidien de dimension 3 (les démonstrations sont données dans l'article groupe alterné). On peut, à l'aide de cette théorie, démontrer rigoureusement l'existence d'un solide de Platon, contenant 12 sommets, 30 arêtes et 20 faces, globalement invariant par un groupe de rotations, copie du groupe alterné de degré 5. Les faces de ce polyèdre sont des triangles équilatéraux.

Le groupe de symétrie complet est isomorphe au produit direct du groupe alterné par le groupe cyclique d'ordre 2, qui forme bien un groupe d'ordre 120.[7]

Groupe de symétrie

L'article groupe alterné montre que le groupe des rotations d'un icosaèdre est le groupe alterné de degré 5. Cette démonstration assure au passage l'existence d'un solide de Platon à 12 sommets. Il reste encore à établir le groupe de symétrie, c'est-à-dire celui contenant non seulement les isométries directes, ou encore de déterminant égal à 1, mais toutes les isométries. Pour déterminer ce groupe, trois lemmes sont utiles :

  • Soit H le groupe des rotations d'un polyèdre, le groupe symétrique G est soit H, soit un groupe d'ordre le double de celui de H :
Si le groupe symétrique ne contient pas d'isométrie de déterminant différent de 1, alors le groupe symétrique est H. C'est le cas, par exemple pour le groupe du tétraèdre régulier. Dans le cas contraire, la seule valeur possible du déterminant est -1. En effet, une isométrie est soit une rotation, son déterminant est égal à 1, soit une isométrie de déterminant égal à -1 (cf Automorphisme orthogonal).
Si le groupe G est différent de H, l'application de G dans {-1, 1}, qui à un élément du groupe associe son déterminant est un morphisme de groupe surjectif. L'ordre de l'image est égal à 2, le noyau est égal à H, ce qui montre que 2 que multiplie l'ordre de H, est égal à celui de G, ce qui termine la démonstration du lemme.

Si le groupe de symétrie contient une isométrie de déterminant égal à -1, deux cas se présentent. Soit il existe une isométrie de déterminant égal à -1 qui commutent avec tous les éléments de H, alors le groupe symétrique G est le produit direct de H et d'un groupe cyclique d'ordre 2, soit un tel élément n'existe pas et G est le produit semi-direct des deux groupes précédents. Une seule partie de cette propriété nous intéresse ici.

  • Avec les notations précédentes, s'il existe une isométrie σ de déterminant égal à -1 et qui commute avec tous les éléments de H, alors G est isomorphe au produit direct de H et du groupe cyclique d'ordre 2 :
Il suffit de construire l'isomorphisme de groupe. On incarne le groupe cyclique d'ordre 2 avec le groupe C2 égal à {0, 1}, équipé de l'addition de Z/2Z. Soit p l'ordre de σ, on remarque que σp est égal à l'identité et possède en conséquence un déterminant égal à 1 ce qui montre que p est un divisible par un multiple de 2. On note r la plus grande puissance de 2 qui divise p. Soit τ l'automorphisme égal à σp/r, cet automorphisme commute avec tous les éléments de H et possède un déterminant égal à -1, car l'entier p/r n'est pas divisible par 2. Soit φ l'application de HxC2 qui à (h, n) associe le produit de τn par h. On remarque que φ est bien un morphisme dont l'image est un groupe contenant à la fois H et τ qui n'est pas dans H car son déterminant est égal à -1. L'image est un sous-groupe de G dont l'ordre est strictement plus grand que la moitié de celui de G. Le théorème de Lagrange montre que l'image de φ est égale à G. L'application φ est un morphisme surjectif entre deux groupes finis de mêmes ordres, c'est un isomorphisme. L'existence de cet isomorphisme termine la démonstration.

Il ne reste plus qu'à trouver l'isométrie de déterminant égal à -1, qui commute avec tous les éléments de A5 et qui laisse invariant l'icosaèdre. On démontre ici un lemme un peu plus puissant, aussi utile pour le paragraphe suivant. On appelle e1 un vecteur de norme 1 situé dans l'axe d'une rotation ρ1 d'un demi-tour. Cette rotation est choisie dans le groupe des rotations de l'icosaèdre. Une rotation d'un demi-tour est une rotation involutive. Le groupe alterné d'ordre 5 contient de telles involutions, elles sont toutes de la forme (ab)(cd), où a, b, c et d sont quatre éléments distincts pris dans l'ensemble {1, 2, 3, 4, 5}. Pour les notations, voir Groupe symétrique.

  • Il existe une base orthonormale (e1, e2, e3) telle que les rotations d'un demi-tour autour d'un axe dirigé par n'importe quel vecteur de la base soient toutes dans le groupe des rotations :

Cette propriété peut se démontrer en établissant que les coordonnées du paragraphe précédent définissent bien un icosaèdre. Il est aussi possible de procéder directement avec des techniques issues de la théorie des groupes.

Soit (ab)(cd), l'équivalent de ρ1 dans le groupe alterné de degré 5. On remarque que l'élément (ac)(bd) est d'ordre 2 et commute avec (ab)(cd), on en déduit l'existence d'une rotation d'un demi-tour ρ2 qui commute avec ρ1. Montrons qu'un vecteur e2, directeur de l'axe de ρ2 et de norme 1, est orthogonal à e1. Comme ρ1 et ρ2 commute, on a :
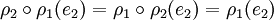
\rho_2\circ\rho_1(e_2) = \rho_1\circ\rho_2(e_2) = \rho_1(e_2)\;
Autrement dit, ρ1(e2) est laissé stable par ρ2, ce qui montre que ce vecteur est colinéaire à e2 et de norme 1. Ce vecteur est soit égal à e2 soit à -e2. La valeur e2 est impossible car ce vecteur serait colinéaire à e1. Il existerait un vecteur directeur, à la fois de l'axe de ρ1 et de celui de ρ2, ce qui montre que ces deux rotations seraient confondus. Or ces deux éléments sont des copies de (ab)(cd) et de (ab)(cd), qui ne le sont pas. On en déduit que ρ1(e2) est égal à -e2, ce qui montre que e2 est perpendiculaire à e1. Il est simple de vérifier que la composition de ρ1 et de ρ2 est une rotation d'un demi-tour, d'axe dirigé par un vecteur e3, orthogonal à e1 et e2 et qui peut être choisi de norme 1.

Une fois les trois lemmes établis, il devient aisé de démontrer la proposition de la boite déroulante. Il suffit de montrer que l'homothétie de rapport -1 est élément du groupe de symétrie.

  • Le groupe symétrique de l'icosaèdre régulier convexe est le produit direct du groupe alterné de degré 5 et du groupe cyclique d'ordre 2 :
Soit s un sommet quelconque de l'icosaèdre, montrons que -s est aussi élément de l'icosaèdre. Soit Δ l'axe d'une rotation d'un demi-tour, élément du groupe des rotations et tel que l'intersection de Δ et avec une arête contenant s, soit non vide. Le groupe contient une rotation d'un demi-tour d'axe orthogonal à Δ. L'image de s par cette rotation est -s.
L'application, qui à s associe -s laisse globalement invariant l'icosaèdre. C'est une isométrie du groupe symétrique, commutant avec tous les éléments du groupe des rotations et de déterminant égal à -1. Le deuxième lemme permet de conclure.
 

Voir aussi

Notes

  1. ↑ F. Buekenhout M. Parker The Number of Nets of the Regular Convex Polytopes in Dimension ⇐4 Disc. Math. 186, 69-94, 1998
  2. ↑ Albrecht Dürer Géométrie Présentation et traduction de Jeanne Peiffer Seuil- Paris 1995 p 31 (ISBN 2020124270)
  3. ↑ P. Cromwell, Peter Polyhedra Cambridge University Press p 53 (1997) (ISBN 0521664055)
  4. ↑ Une analyse graphique est proposée sur le site R. Ferréol Icosaèdre
  5. ↑ Ces résultats sont présentés dans : E. W. Weisstein Icosahedron le site MathWorld
  6. ↑ On trouve ces calculs, par exemple dans : F. Buekenhout M. Parker The Number of Nets of the Regular Convex Polytopes in Dimension ⇐4. Disc. Math. 186 pp 69-94, 1998
  7. ↑ Cette approche est souvent traitée comme une application de la théorie des groupes finis : J. S. Lomont Applications of Finite Group Dover Publications 1993 p 82 (ISBN 0486673766)

Lien interne

Liens externes

Sur les autres projets Wikimedia :

Références

  • (en) P. R. Cromwell Polyhedra Cambridge University Press 1999 (ISBN 0521664055)
  • (en) M. J. Wenninger Dual Models Cambridge University Press 2003 (ISBN 0521543258)


Solides géométriques
Les polyèdres
Les solides de Platon
Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre
Les solides d'Archimède
Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre
Les solides de Kepler-Poinsot
Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre
Les solides de Catalan
Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre
Les solides de Johnson
Les solides de révolution
Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Icosa%C3%A8dre ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Icosaédre de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Icosaedre — Icosaèdre Icosaèdre Type Polyèdre régulier Faces Triangle Éléments :  · Faces  · Arêtes  · Sommets  · Caractéristique   20 30 12 2 Faces par sommet 5 Sommets par face …   Wikipédia en Français

  • Icosaèdre — Type Polyèdre régulier Faces Triangle Éléments :  · Faces  · Arêtes  · Sommets  · Caractéristique …   Wikipédia en Français

  • icosaèdre — [ ikozaɛdr ] n. m. • 1557; lat. icosahedrum, gr. eikosaedron, de eikosi « vingt » ♦ Géom. Polyèdre limité par vingt faces. Adj. ICOSAÉDRAL, ALE, AUX . ● icosaèdre nom masculin (bas latin icosahedrum, du grec eikosaedros, à vingt faces) Solide à… …   Encyclopédie Universelle

  • ICOSAÈDRE — s. m. T. de Géom. Corps solide qui a vingt faces. La surface de l icosaèdre est composée de vingt triangles équilatéraux …   Dictionnaire de l'Academie Francaise, 7eme edition (1835)

  • ICOSAÈDRE — n. m. T. de Géométrie Corps solide qui a vingt faces. La surface de l’icosaèdre est composée de vingt triangles équilatéraux …   Dictionnaire de l'Academie Francaise, 8eme edition (1935)

  • icosaèdre — (i ko za è dr ) s. m. Terme de géométrie. Corps solide qui a vingt faces. La surface de l icosaèdre régulier est composée de vingt triangles équilatéraux. ÉTYMOLOGIE    Le grec signifie, vingt (voy. vingt), et, face …   Dictionnaire de la Langue Française d'Émile Littré

  • icosaèdre — ikosaedras statusas T sritis fizika atitikmenys: angl. icosahedron vok. Ikosaeder, m rus. икосаэдр, m pranc. icosaèdre, m …   Fizikos terminų žodynas

  • Icosaedre tronque — Icosaèdre tronqué Icosaèdre tronqué Type Solide d Archimède Faces Hexagones et Pentagones Éléments :  · Faces  · Arêtes  · Sommets  · Caractéristique   32 90 60 2 Faces par sommet …   Wikipédia en Français

  • Icosaèdre Tronqué — Type Solide d Archimède Faces Hexagones et Pentagones Éléments :  · Faces  · Arêtes  · Sommets  · Caractéristique   32 90 60 2 Faces par sommet …   Wikipédia en Français

  • Icosaèdre tronqué — Type Solide d Archimède Faces Hexagones et Pentagones Éléments :  · Faces  · Arêt …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”