Isoperimetrie

Isoperimetrie

Isopérimétrie

La forme d'une bulle de savon est une réponse à une question d'isopérimétrie. Sa géométrie est sphérique car c'est le solide qui englobe le plus vaste volume dans une surface de mesure donnée.

En géométrie plane, l'isopérimétrie traite, en particulier, la question de trouver la surface la plus vaste possible, pour un périmètre donné. La réponse est intuitive, c'est le disque. Ce problème, d'apparence anodin, fait appel à des théories sophistiquées pour obtenir une démonstration rigoureuse. À cet égard, il ressemble un peu au théorème de Jordan, indiquant qu'une boucle la plus simple possible (sans croisement) divise un plan en deux parties, l'intérieur de la boucle qui est borné, et l'extérieur qui ne l'est pas. En conséquence, on simplifie parfois le problème isopérimétrique en limitant les surfaces autorisées. Par exemple, on cherche le quadrilatère ou le triangle d'aire la plus plus vaste possible, toujours pour un périmètre donné. Les solutions respectives sont le carré et le triangle équilatéral. De manière générale, le polygone à n sommets ayant la plus grande surface, à périmètre donné, est celui qui se rapproche le plus du cercle : c'est le polygone régulier.

L'isopérimétrie ne se limite pas à ces questions. On recherche aussi une zone d'aire la plus vaste possible pour un périmètre donné, avec des géométries différentes. Par exemple, dans le cas d'un demi-plan, la réponse est le demi-disque. La question du solide de plus grand volume, enveloppé dans une surface de mesure fixée est naturellement dans le domaine de l'isopérimétrie. La bulle de savon, qui cherche à envelopper un volume d'air donné dans la surface la plus petite possible, indique la solution : une sphère.

Ce concept donne naissance à une famille de théorèmes, dit isopérimétriques, à des majorations dites inégalités isopérimétriques, ainsi qu'à un rapport, appelé quotient isopérimétrique. En dimension 2, l'inégalité isopérimétrique indique qu'une surface de périmètre p et d'aire a vérifie la majoration suivante :

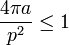
\frac {4 \pi a}{p^2} \le 1

Le terme de gauche, est appelé quotient isopérimétrique, il est égal à 1 si, et seulement si la surface est un disque.

Si l'origine de cette question date d'au moins 2 900 ans, ce n'est qu'en 1895, à l'aide de méthodes dérivées du théorème de Minkowski que la question est définitivement résolue sous sa forme antique. Ces méthodes permettent de démontrer le théorème isopérimétrique et de le généraliser à des dimensions supérieures dans le cas d'une géométrie euclidienne.

Cet article traite uniquement des aspects élémentaires de cette question. Des éléments de réponse, faisant usage d'outils mathématiques plus sophistiqués, sont proposés dans l'article Théorème isopérimétrique.

Sommaire

Fragments d'histoire

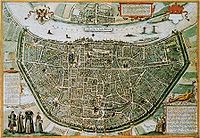
Didon applique le théorème isopérimétrique pour l'achat du terrain à l'origine de la fondation de Carthage.[1]

La légende[2] raconte que la ville de Carthage, fut fondée 814 av. J.-C. par la princesse phénicienne Elissa, surnommée Didon. Elle demanda au roi de Numidie Iarbas l'octroi d'un terrain pour s'y installer. Iarbas, réticent, lui accorda le droit de choisir un lopin de terre que pourrait contenir la peau d'un bœuf. La rusée Didon découpa en une fine lamelle la peau, qui devint une longue lanière de 4 km de long[3]. Elle fit étendre cette lanière sur un demi-cercle dont les deux extrémités touchaient la côte, rectiligne à l'endroit où elle se trouvait[4]. La reine avait intuitivement trouvé la solution au problème isopérimétrique dans un demi-plan euclidien. Ce problème est résolu lorsqu'est trouvée la surface la plus grande possible, pour un périmètre donné[5]. Le demi-cercle est en effet la courbe que doit suivre la lanière pour délimiter la plus grande surface possible, dans ce cas particulier.

La méthode, consistant à mesurer une surface à l'aide de son périmètre, est fréquente durant l'antiquité grecque. Homère indique que la ville de Troie fait 10 200 pas, indiquant par là qu'en faire le tour demande une marche de 10 200 pas[6]. La solution du problème isopérimétrique dans le plan euclidien est connue par certains depuis le Ve siècle av. J.-C., au moins pour le cas du polygone à n cotés[7]. Il porte le nom de théorème isopérimétrique. À l'époque des grecs, tous ne semblent pas au courant de ce résultat et de ses conséquences. Proclos (412-495) mentionne le cas de tricherie de géomètres datant de cette époque. Des terrains étaient divisés en différents lopins de même périmètre mais de surfaces différentes, les géomètres, responsables du partage, obtenaient les plus grosses parcelles. La supercherie fut découverte au moment des moissons, dont l'abondance est proportionnelle à la surface et non au périmètre[8].

Théon d'Alexandrie (335- 405) et Pappus IVe siècle attribue à Zénodore IIe siècle av. J.-C. les premières démonstrations[9]. Il prouve que parmi tous les polygones à n cotés et même périmètre, seul celui régulier est candidat à être la réponse au problème isopérimétrique. Il découvre aussi que le disque d'un périmètre donné possède une surface supérieure à celle de n'importe quel polygone régulier. Il aurait aussi démontré que la sphère est le solide ayant un plus grand volume que tout polyèdre de même surface[10].

Les mathématiques grecs n'ont pas les moyens d'aller au delà. Leurs démonstrations restent partielles, même si leurs auteurs n'ont pas conscience de l'aspect incomplet des preuves. Ils ne disposent pas non plus des outils mathématiques qui auraient permis d'aller plus loin. Les mathématiciens arabes s'approprient le savoir des grecs sur cette question. Abū Ja'far al-Khāzin écrit un traité résumant tout le savoir de son époque sur l'isopérimétrie[11]. Ils développent les moyens d'aller plus loin. Nasir ad-Din at-Tusi un mathématicien du XIIIe siècle développe, dans son traité du quadrilatère[12], suffisamment la trigonométrie pour présenter des preuves complètes dans le cas des triangles ou des rectangles.

Il faut ensuite attendre les mathématiques européennes du XIXe siècle pour d'autres progrès. En 1836, Jakob Steiner obtient un premier résultat nouveau. Sous réserve d'admettre l'existence d'une solution en dimension 2, alors cette solution est nécessairement le disque[13]. Pour une preuve complète en dimension 2, il faut attendre les travaux de Karl Weierstrass et Hermann Minkowski, elle devient rigoureuse vers 1895[14]. Cette partie de l'histoire est traitée dans l'article théorème isopérimétrique.

Définitions et premières propriétés

Dimension 2

Soit Pn un polygone à n cotés, où n désigne un entier plus grand que 2, p son périmètre et an son aire. Dans ce cas particulier, le théorème isopérimétrique s'exprime sous la forme suivante :

Théorème isopérimétrique pour un polygone —  L'aire de Pn est plus petite que celle d'un polygone régulier à n cotés et de périmètre p. Un disque de périmètre p possède une aire strictement plus grande que celle de Pn.

Ce théorème peut s'exprimer sous la forme d'une inégalité :

Inégalité isopérimétrique pour un polygone —  On dispose de l'inégalité suivante :

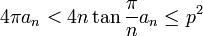
4\pi a_n < 4n \tan \frac {\pi}na_n \le p^2

Cette propriété est très générale, elle reste vraie pour toute surface d'aire a, ayant un bord rectifiable de longueur p, c'est-à-dire que le bord est une courbe qui possède une longueur finie.

Théorème isopérimétrique dans un espace euclidien de dimension 2 —  L'aire a est plus petite que celle du disque de même périmètre p, ce qui donne lieu à la majoration suivante, dite inégalité isopérimétrique. L'égalité a lieu uniquement si la surface est un disque.

p^2 - 4\pi a \ge 0

Ce théorème donne lieu à une définition :

Quotient isopérimétrique —  Le quotient q défini par l'égalité suivante, est appelé quotient isopérimétrique :

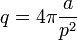
q = 4\pi \frac {a}{p^2}

On peut interpréter ce quotient comme le carré du rapport entre le rayon du cercle ayant même aire sur le rayon du cercle ayant même périmètre. L'inégalité isopérimétrique est équivalente à dire que q est inférieur à 1, le cas d'égalité n'ayant lieu que si la surface est un disque.

Dimension 3

En dimension 3, on ne peut approcher de plus en plus précisément la sphère par des polyèdres réguliers convexes. Il n'en existe que 5, appelé solide de Platon. Le résultat général reste néanmoins vrai :

Théorème isopérimétrique dans un espace euclidien de dimension 3 —  Soit un solide mesurable au sens de Lebesgue ayant un bord mesurable, son volume est plus petit que celui de la boule dont la sphère a même aire.

Remarque: Ici le bord du solide est une surface comme la sphère est le bord de la boule.

L'inégalité isopérimétrique s'exprime à l'aide d'un quotient isopérimétrique q. Elle indique que ce coefficient est toujours inférieur à 1 et le cas d'égalité n'a lieu que pour la sphère. Le coefficient q s'exprime sous la forme suivante, si v désigne le volume du solide et s l'aire du bord de ce solide :

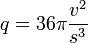
q = 36\pi \frac {v^2}{s^3}

Cette formule est commentée à travers l'exemple de l'icosaèdre, à la suite de l'article.

Résultats élémentaires

Préambule

Il n'est pas nécessairement intuitif de déterminer à l'oeil la figure qui possède la plus grande aire.
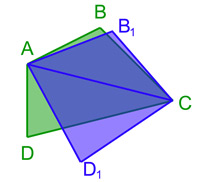
Un polygone non convexe ne peut pas être une réponse au problème isopérimétrique.

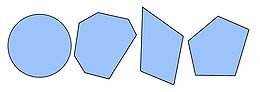
Le schéma de gauche[15] représente quatre figures, dont trois polygonales et toutes de même périmètre. Il n'est pas toujours évident de repérer immédiatement celle de plus grande aire. L'histoire montre même que pour certains grecs, l'idée que deux régions, délimités par deux courbes de même longueur, puissent avoir des aires différentes était contre intuitive.

Si, dans le cas général, la démonstration est suffisamment complexe pour avoir demandé près de 3 000 ans d'efforts, traiter uniquement le cas des polygones est plus simple. Des solutions élémentaires sont connues depuis l'antiquité, même si elles restent partielles. Elles sont présentées ici dans un langage moderne.

La lettre n désigne un entier plus grand que 2 et p un nombre réel strictement positif. La question à résoudre est de trouver, s'il existe, le polygone à n cotés et de périmètre p, ayant la plus grande aire. On peut remarquer qu'il suffit de chercher uniquement dans les polygones convexes. Le terme convexe signifie ici qu'un élastique entourant le polygone est toujours en contact avec sa frontière. Considérons, en effet, un polygone non convexe P1, par exemple celui illustré sur la figure de droite, en bleu. Son enveloppe convexe, c'est-à-dire la figure ayant pour frontière celle donnée par un élastique entourant le polygone P1, est un nouveau polygone P2, cette fois convexe. Le polygone P2 correspond à celui contenant les zones bleue et verte sur la figure. Son aire est strictement plus grande et son périmètre strictement plus petit. Une dilatation d'un rapport bien choisi, nécessairement supérieur à 1, appliquée à P2 définit un nouveau polygone P3 de même périmètre que celui de P1. L'aire de P1 est strictement plus petite que celle de P2, elle même strictement plus petite que celle de P3. Le polygone P3 est de même périmètre que P1 et d'aire strictement plus grande. On en déduit que P1 n'est pas un candidat pour répondre au problème isopérimétrique.

Quadrilatère

Ce cas correspond à celui qui peut être résolu intégralement sans autre savoir que celui des mathématiciens grecs.

Cas du quadrilatère — L'unique quadrilatère de périmètre p et d'aire maximale pour ce périmètre est le carré de côté p/4.

L'aire d'un carré est égale à p2/16. Le dénominateur 16 est plus grand que 4π. On en déduit, si a4 est l'aire d'un quadrilatère de périmètre p :

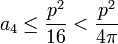
a_4 \le \frac {p^2}{16} < \frac {p^2}{4\pi}

La démonstration utilise un lemme, utile pour le problème isopérimétrique de n'importe quel polygone :

Lemme 1 — Parmi tous les triangles de base AB, de dernier sommet C et de périmètre p, celui tel que la distance AC est égale à CB est d'aire strictement plus grande que toutes les autres. Le triangle est alors nécessairement isocèle.[16]

Détail de la démonstration

Dans un premier temps, le lemme doit être démontré, il est l'ossature de nombreuses démonstrations de cet article.

  • Parmi tous les triangles de base AB, de dernier sommet C et de périmètre p, celui tel que la distance AC est égale à CB est d'aire strictement plus grande que toutes les autres :
Problème isopérimétrique (triangle).jpg
Le triangle du lemme est illustré en noir sur la figure de gauche. On suppose qu'il possède deux cotés de longueurs inégales, ici AC et BC. Soient h la hauteur du triangle, par rapport à la base AB, illustrée en vert sur la figure et D le point à même hauteur que C et situé sur la droite perpendiculaire à AB et qui coupe AB en son milieu. Soit δ la distance entre D et C. Par hypothèse, la longueur δ est non nulle, sinon AC et BC seraient de même longueur.
La première étape consiste à montrer que le triangle ABD est de même aire que le triangle initial ABC et de périmètre strictement plus petit. Comme l'aire de ces deux triangles est égale au produit de la distance entre A et B et de la moitié de h, ces deux aires sont bien égales. Il reste à montrer que le périmètre de BDA est plus petit que celui de BCA. Il suffit pour cela d'appliquer le principe de Fermat. Un rayon lumineux issu du point A, reflétant sur un miroir illustré par la droite violette Δ (correspondant à la droite parallèle à AB et passant par C et D) et éclairant le point B, utilise le plus court chemin, qui passe par D. Pour le démontrer il suffit de considérer le point E symétrique de B par rapport à l'axe Δ. La distance entre E et D est la même que celle entre B et D, on en déduit que la distance ADE est la même que ADB. De même, la distance ACE est la même que ACB. Or, il est bien évident que ADE est plus court que ACE, car les trois points A, D et E sont alignés.
Problème isopérimétrique (triangle 2).jpg
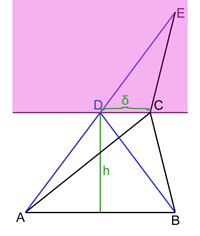
La deuxième étape consiste à constuire un triangle ABF de même périmètre et d'aire plus grande que le triangle initial. On considère le point F, sur la droite perpendiculaire à AB et passant par D (en vert sur la figure de droite), et tel que la longueur des deux segments AF et FB soit la même que celle des deux segments AC et CB. Comme le triangle AFB et le triangle ACB ont même périmètre, strictement plus grand que celui du triangle ADB, le point F est plus haut que D, autrement dit AF est strictement plus grand que AD, ou encore l'aire du triangle AFB est strictement plus grande que celle du triangle ADB. L'aire supplémentaire est illustrée en rose. On a bien construit un triangle AFB de même périmètre que ACB et d'aire strictement plus grande, ce qui termine la démonstration. On remarque de plus que la base AB n'a pas été modifiée.

Une fois ce lemme établi, on procède à partir d'un quadrilatère convexe Q, de sommets ABCD et de périmètre p. Si ce polygone n'est pas un carré, on va montrer que le carré de périmètre p est d'aire strictement plus grande. Pour arriver à nos fins, il est possible de procéder à l'aide d'un losange, qui présente une étape intermédiaire de la démonstration.

  • Si le quadrilatère Q n'est pas un losange, il existe un losange Q1 de même périmètre et d'aire strictement supérieure :
Problème-isopérimétrique-(quadrilatère 1).jpg
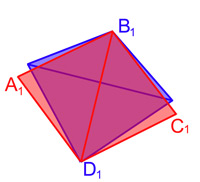
Problème-isopérimétrique-(quadrilatère 2).jpg
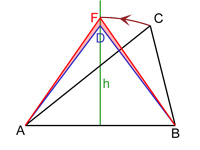
Cette étape est elle même décomposée en deux étapes :
La première est illustrée sur la figure de gauche, Q est représenté en vert. Le quadrilatère ABCD possède nécessairement deux cotés adjacents de longueurs distinctes, sinon ABCD serait un losange. Quitte à modifier l'ordre des lettres associées à chaque sommet, on peut toujours supposer que AB n'est pas égale à BC. On utilise le lemme pour construire le point B1. Le triangle AB1C possède un périmètre égal à celui de ABC et est de plus isocèle. On construit de la même manière D1. Le quadrilatère bleu est d'aire strictement supérieure au quadrilatère initial et il dispose d'une propriété utile pour la suite. La distance AB1 est égale à B1C, il en est de même pour AD1 et D1C. Autrement dit, les deux longueurs D1AB1 et B1CD1 sont toutes deux égales à p/2.
La deuxième étape,illustrée à droite, est l'exact analogue sur le quadrilatère AB1CD1, mais cette fois sur les triangles D1AB1 et B1CD1. A l'aide du quadrilatère bleue, on construit maintenant le rouge, noté A1B1C1D1. La longueur du coté A1B1 est la moitié de la longueur D1AB1 soit p/4. Ce raisonnement s'applique au quatre cotés, tous égaux, ce qui montre que le quadrilatère rouge est un losange.
Le losange rouge, noté L est d'aire supérieure au quadrilatère bleu, lui-même d'aire strictement supérieure à celle du quadrilatère vert et tous sont de même périmètre. À partir d'un quadrilatère qui n'est pas un losange, on a bien construit un losange de même périmètre et d'aire strictement supérieure, ce qui termine la démonstration.
Problème-isopérimétrique-(carré).jpg

Pour terminer, il suffit de montrer que si le losange L n'est pas un carré, alors le carré C, de même périmètre est d'aire strictement supérieure.

  • Parmi les losanges de périmètre p, le carré est l'unique dont l'aire est maximale:
L'aire du losange est égale au produit de sa base, ici la longueur de A1D1, par sa hauteur. On définit le point B2 comme le point à une distance égale à celle de A1B1 et tel que A1D1 et A1B2 forment un angle droit. Du losange rouge de la démonstration précédente, on passe à un losange bleu A1B2C2D1 qui se trouve être le carré C de périmètre p. La hauteur de ce carré par rapport à la base A1D1 est strictement plus grande que celle du losange L, si celui-ci n'était pas un carré, ce qui montre que l'aire du carré est strictement plus grande et termine la démonstration.

En résumé, si Q n'est pas un losange, on construit un losange L de même périmètre et d'aire strictement supérieure. Puis, si L n'est pas le carré de périmètre p, on remarque que l'aire de L est strictement plus petite que celle du carré C. Cette double construction montre bien que le carré C est d'aire plus grande que celles de tous les quadrilatères de périmètre p et que, si un quadrilatère de périmètre p possède la même aire que celle du carré C, c'est que ce quadrilatère est aussi un carré de périmètre p.

 

Polygone quelconque

Le cas du polygone quelconque se traite un peu différemment. La proposition suivante peut être démontrée à l'aide de techniques comparables à celle du paragraphe précédent :

Cas du polygone quelconque — Un polygone de n cotés, de périmètre p et d'aire maximale pour ce périmètre est régulier.

Si an désigne l'aire du polygone régulier, on dispose des inégalités isopérimétriques :

a_n \le \frac {p^2}{4n\tan\left(\frac {\pi}n\right)} < \frac {p^2}{4\pi}

Une partie significative de la démonstration consiste à établir le lemme suivant, attribué à Zénodore. Le calcul de la surface du polygone régulier est l'œuvre d'Archimède. Si les idées sont antiques, la rédaction proposée ici est moderne, elle diffère totalement des preuves qui nous ont été rapportées.[17]

Lemme 2 —  Si un polygone à n cotés est solution du problème isopérimétrique, les angles entre deux cotés partageant un même sommet sont égaux.

Détail de la démonstration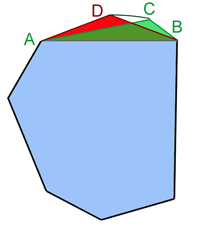
Problème-isopérimétrique-(coté).jpg

L'objectif est de montrer qu'un polygone P à n cotés et de périmètre p n'est pas d'aire maximale s'il n'est pas régulier. Comme pour le paragraphe précédent et pour les mêmes raisons, on suppose que P est convexe. Il suffit donc de montrer que soit les cotés ne sont pas tous de même longueurs, soit ils le sont mais les angles entre deux arêtes partageant un même sommet ne sont pas tous égaux. Ce qui divise la démonstration en deux parties. Le premier résultat s'exprime ainsi :

  • Un polygone ayant deux arêtes de longueurs distinctes n'est pas solution du problème isopérimétrique :
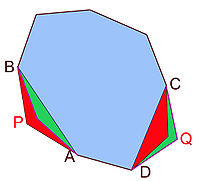
On suppose que notre polygone P possède deux arêtes de longueurs distinctes. On remarque qu'il est alors possible de trouver deux arêtes partageant un même sommet. En effet, si toutes les arêtes partageant un même sommet sont de même longueur, de proche en proche on remarque qu'elles sont toutes de même longueur.
Le cas étudié est illustrée sur la figure de droite, le triangle ACB, formé par les deux arêtes de longueurs différentes est illustré en vert, ses sommets sont notés. Les deux arêtes AB et CB partageant le sommet sont de longueurs différentes, le lemme 1 du paragraphe précédent montre qu'il est possible de construire un deuxième triangle, illustré en rouge, de même base AB et de sommet D tel que les triangles ACB et ADB soient de même périmètre et tel que le triangle rouge ADB soit d'aire strictement supérieure à celle du vert.
Le polygone P1, ayant les mêmes sommets que P, à l'exception de C, qui est remplacé par D possède un périmètre égal à p et inchangé. En effet, la longueur AC + CB est, par construction, égal à la longueur AD + DB. En revanche, l'aire de P1 est strictement supérieure à celle de P. Pour s'en persuader, il suffit de remarquer que l'aire bleue n'est pas modifiée. En revanche, l'aire verte retranchée est remplacée par l'aire rouge, strictement plus grande d'après le lemme 1.
  • Un polygone n'ayant que des arêtes de même longueur, mais dont deux angles au moins diffèrent, n'est pas solution du problème isopérimétrique :
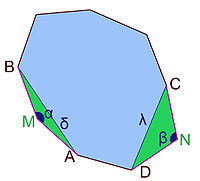
Problème isopérimétrique général 1.jpg
Problème isopérimétrique général 2.jpg

On suppose maintenant que les angles associés aux sommets ne sont pas tous égaux. On suppose même, dans un premier temps l'existence de deux angles α et β tel que β est strictement plus petit que α et que leurs sommets associées ne sont pas adjacents, c'est-à-dire que ces deux sommets ne forment pas une arête du polygone. Cette situation est illustrée sur la figure de gauche, qui permet en même temps de définir les points A, B, C, D, M et N. Comme l'indique la figure, les distances δ et λ sont respectivement celles de AB et de CD. Puisque α est strictement plus grand que β, δ est strictement plus grand que λ.

Sans modifier le périmètre de P, on construit un nouveau polygone P1, ayant le même nombre de sommets n, même périmètre, mais une surface strictement plus grande, ce qui montre la proposition. Le polygone P1 est illustré à droite.

Construction des triangles APB et CQD :
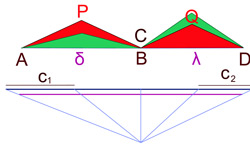
Problème isopérimétrique général 3.jpg
On considère un segment, en bleu sur la figure de droite, de longueur 4 fois celle d'une arête de P1. Ce segment possède la même longueur que la somme des longueurs des 4 arêtes AM, MB, CN et ND. Cette longueur est choisie égale à la somme des distances séparant A et P, P et B, C et Q, Q et D. Ainsi la substitution des triangles verts par les triangles rouges ne modifie pas le périmètre du polygone.
Soit r la proportion δ/(δ + λ), on découpe le segment en deux parties, l'une de proportion r et l'autre de (1 - r). On obtient ainsi deux segments dont la somme des longueurs est égale à 4 fois celle d'une arête et ces deux segments sont proportionnels à deux segments de longueurs δ et λ. Les deux segments sont divisées en deux parties égales, on obtient 4 segments, deux de longueur nommée c1 et les deux autres sont nommés c2. L'ordre est choisi tel que c1 soit supérieur à c2. Ce découpage est illustré par une méthode permettant de le construire à la règle et au compas sur la figure de droite. Le segment violet est de longueur égale à δ + λ.
Soit P le point à distance c1 de A et de B et Q le point à distance c2 de C et D. Par construction les triangles APB et CQD sont isocèles, ils sont de plus semblables. En effet, le rapport des distances AB sur AP est par construction égal à CD sur CQ. Il existe deux choix de points pour P et Q, on choisit bien sûr ceux qui rendent P1 convexe. On peut maintenant troquer les deux triangles isocèles verts par deux triangles isocèles rouges sans pour autant modifier le périmètre. Les deux triangles isocèles rouges sont semblables, ce qui n'est pas le cas des triangles verts, sinon, les angles α et β seraient égaux. Ce caractère semblable permet de montrer que l'aire de P est strictement plus petite que celle de P1. C'est l'objet de la démonstration suivante.
Comparaison des aires de P et P1 :
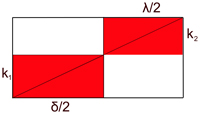
Problème isopérimétrique général 4.jpg
Comme la zone en bleu sur les deux première figures de cette boite déroulante n'a pas été modifiée, cela revient à montrer que la somme des aires des triangles verts est plus petite que la somme des aires des triangles rouges.
Pour comparer les aires, on les découpe et les places dans un rectangle. Procédons d'abord pour le rectangles rouges. Soient k1 et k2 leurs hauteurs. Si l'on découpe les triangles selon leurs hauteurs, on obtient pour chacun deux triangles rectangles de cotés de longueur ki, où i varie de 1 à 2. On peut les assembler pour former des rectangles, comme indiqué sur la figure de droite, car les triangles rouges sont isocèles. On remarque que les deux diagonales sont alignées car les triangles sont semblables.
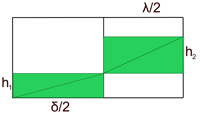
Problème isopérimétrique général 5.jpg
Le même traitements sur les triangles verts donne le résultat illustré à gauche, si h1 et h2 désigne les hauteurs des deux triangles. On remarque que, cette fois-ci, h1 est plus petit que k1, le premier rectangle vert est plus aplati que son équivalent rouge. En effet, si k1 était plus petit que h1, alors k2 serait encore plus petit. En effet, λ est plus petit que δ et les deux triangles rouges sont semblables. La somme des arêtes des triangles rouges seraient strictement plus petites que celle des arêtes des triangles verts, ce qui n'est pas possible, par construction ces sommes sont égales. On peut remarquer de plus que les deux diagonales des triangles verts sont de longueur celle du arête du polygone P1 et que leur somme est égale à la somme des diagonales des rectangles rouges. On en déduit que h1 + h2 est strictement plus petit que k1 + k2.
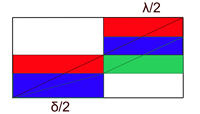
Problème isopérimétrique général 6.jpg
La superposition des deux figures donne le schéma en bas à droite. Il existe une zone verte non recouverte par la zone rouge (Les zones recouvertes par les rectangles rouges et verts sont illustrées en bleu). Comme δ est strictement plus grand que λ, il suffit de faire glisser cette zone sur la gauche pour que le vert soit entièrement recouvert. Il reste alors une zone rouge non recouverte, en haut à droite, ce qui montre que l'aire des triangles rouges est strictement supérieure à celle des triangles verts.

On peut maintenant traiter le cas général du paragraphe. C'est-à-dire le cas où les angles α et β sont côte à côte.

  • Un polygone non régulier n'est jamais solution du problème isopérimétrique :
Pour n égal à 4, on trouve une démonstration dans le paragraphe précédent. Pour n égal à 3, un triangle ayant 3 cotés égaux possède nécessairement ses trois angles aussi égaux. Si n est supérieur ou égal à 5, la démonstration précédente montre que, dans le cas d'un polygone régulier, l'angle associé au premier sommet est égal à celui associé à n'importe quel sommet, à l'exception du deuxième est du dernier. L'angle associé au quatrième sommet, qui n'est jamais le dernier, car n est plus grand ou égal à 5, est le même que celui associé au premier et deuxième sommet. Le premier et deuxième sommet ont donc des angles égaux. Le même raisonnement, en utilisant le troisième sommet, montre que les angles associés aux premier et dernier sommet sont aussi égaux.
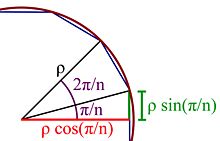
  • Le polygone régulier à n cotés et de périmètre p possède une aire égale à p2/4ntan(π/n) :
Problème isopérimétrique général 7.jpg

On peut calculer simplement le quotient isopérimétrique du polygone régulier. La figure explicative est sur la gauche. Les calculs sont présentés dans l'article Polygone régulier.

Si a est la surface d'un polygone à n cotés de périmètre p, son aire est inférieure à celle du polygone régulier, ce qui démontre la première partie de l'inégalité isopérimétrique. La dérivée de la fonction tangente dans l'intervalle ]0, π/2[ est strictement plus grande que 1, le théorème des accroissements finis montre la deuxième partie de l'inégalité :

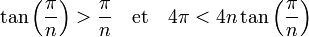
\tan\left(\frac {\pi}n\right) > \frac {\pi}n \quad \text{et}\quad 4\pi < 4n\tan\left(\frac {\pi}n\right)
 

Frontière non polygonale

Le cas de la frontière non polygonale n'est guère plus complexe, pour arriver à un résultat équivalent aux précédents :

Cas de la surface quelconque — Toute surface de périmètre p et d'aire maximale pour ce périmètre est un disque.

L'astuce est l'œuvre de Steiner, qui trouve un procédé de symétrisation, toujours utilisé et qui porte maintenant son nom.

Démonstration de Steiner
Problème isopérimétrique Steiner (1).jpg

On suppose que S est une surface d'aire a et de périmètre p. On suppose de plus que l'aire a est maximale pour le périmètre p. Cette surface est illustrée à gauche, elle possède la forme d'un œuf posé horizontalement. L'objectif est de montrer que, pour éviter toute contradiction, S est nécessairement un disque. La forme initiale choisie n'est pas un disque pour illustrer de manière plus vivante la contradiction.

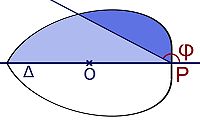
  • Construction de l'axe Δ et du point O :

L'objectif est de couper la figure en deux parties égales et symétrique. On considère tout d'abord un point P de la surface, une demi droite D d'extrémité P, dont l'intersection avec S est réduite au point P. Soit f la fonction de [0, 2π], qui à un angle φ associe l'aire de l'intersection entre S et la zone délimitée par les demi droite D et sa rotation d'angle φ. La valeur f(φ) correspond à l'aire de la zone de couleur bleue foncée sur la figure. On remarque que f(0) est égal à 0 et f(2π) à a. Comme la fonction f est continue, il existe une valeur de φ dont l'image par f est égale à la moitié de la surface de S. Sur la figure, cette valeur de φ est égale à π. Soit Δ la droite associée à cette valeur de φ, elle coupe la surface S en deux parties d'aire égale.

Le point P est un des deux points frontière de S appartenant à Δ, soit Qle deuxième point frontière et O le milieu de ces deux points. Le périmètre de la partie supérieure à Δ de S est le même que le périmètre de la partie inférieure. En effet, si le périmètre était plus petit en haut, la surface de périmètre, au dessus de Δ égale à celle de S, puis en dessous à la rotation d'un demi-tour de la partie supérieure par rapport au point O, aurait exactement la même surface pour un périmètre moindre. Une dilatation de cette surface donnerait une zone de surface strictement plus grande pour un même périmètre. Ceci est impossible car S est choisie maximale. Si S est un disque, l'axe Δ est celui d'un diamètre, O le centre du disque et la zone inférieure la parfaite symétrique de celle supérieure.

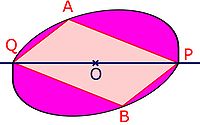
  • Construction du quadrilatère QAPB :
Problème isopérimétrique Steiner (2).jpg

On ne travaille néanmoins pas sur S, mais sur S1, représentée sur la figure de droite. La frontière de la zone inférieure est choisie égale à la rotation d'un demi tour de celle de la zone supérieure. Une rotation étant une isométrie, ni le périmètre ni la surface n'ont été modifiés. L'aire de S1 est aussi maximale pour le périmètre p.

Soit A un point de la frontière de S1 (A différent de P et Q) et B son symétrique par rapport à O. La figure S1 étant symétrique par rapport à O, le point B est aussi sur la frontière de S1 . Les quatre segments QA, AP, PB et BQ coupe la nouvelle surface en 5 parties, 4 lunules de couleur violette sur la figure de droite et un parallélogramme rose.

  • Position de A :
Problème isopérimétrique Steiner (3).jpg

La démonstration sur les quadrilatères montre que le losange de plus grande aire, à isopérimètre est le carré. Cette même démonstration prouve que le parallélogramme de plus grande aire, à isopérimètre et sans modifier la longueur des côtés est le rectangle. Si le parallélogramme QAPB n'est pas un rectangle, il est possible de construire une nouvelle surface S2 en déplaçant les quatre lunules de manière à rendre la zone QAPB rectangulaire, comme illustré sur la figure de gauche.

Si QA et AP n'étaient pas deux segments initialement perpendiculaires, on obtiendrait une nouvelle figure de même périmètre que S et de surface strictement supérieure, ce qui est impossible par hypothèse. Le triangle QAP est donc rectangle en A ce qui, selon le théorème du triangle inscrit dans un demi-cercle place le point A sur le cercle de diamètre [PQ]. Le point A ayant été choisi quelconque sur la frontière de S1 (différent de P ou Q), tous les points de la frontière sont sur le cercle de diamètre [PQ] et S1 est donc un disque. [18]

 

Topologie

À part pour le cas du quadrilatère, les théorèmes établis ne sont pas aussi puissants qu'ils y paraissent. On en prend conscience uniquement vers la moitié du XIXe siècle. Les théorèmes indiquent que si une surface est d'aire maximale elle dessine un polygone régulier ou un disque selon le cas étudié. En revanche, ils n'indiquent pas que le polygone régulier ou bien le disque réalise ce maximum. Cette partie de la démonstration, ce chainon manquant nécessite des outils plus sophistiqués que ceux découverts à l'époque de Steiner. Ils font appel à une branche des mathématiques appelée topologie.

Tous les raisonnements présentés dans cet article, à l'exception de ceux sur le quadrilatère, ont la même structure logique. On montre qu'aucune solution n'est acceptable à l'exception d'une. Ceci ne montre pas que celle qui reste est une solution. Le mathématicien O. Perron illustre la faute logique en faisant observer[19] qu'accepter ce type de preuve reviendrait à permettre de démontrer que 1 est le plus grand des nombres entiers. Si l'entier a est différent de 1, le carré de a est strictement plus grand que a. Le nombre a ne peut donc pas être le plus grand des entiers. L'unique exception parmi les entiers strictement positifs est 1, qui serait alors le plus grand des entiers.

Il est ainsi établi que toute surface de périmètre p et d'aire maximale ne peut être qu'un disque, mais l'énoncé n'implique pas que le disque est de fait une surface maximale, ou encore que le polygone régulier à n cotés est d'aire maximale parmi les polygones à n cotés de même périmètre. Ces deux résultats sont néanmoins vrais, les preuves associées sont proposées dans l'article Théorème isopérimétrique. Dans le cas du triangle, on peut tout de même arriver au résultat en se limitant à l'usage d'une fonction continue de la variable réelle à valeurs réelles.

Cas du triangle
  • Tout triangle de périmètre p et d'aire maximale est équilatéral :

Le lemme 1 montre que si un triangle n'est pas équilatéral, il ne peut être solution du problème isopérimétrique. En effet, si les trois longueurs des trois cotés sont notés a, b et c, le lemme montre que a = b et que b = c est une condition nécessaire pour que le triangle soit d'aire maximal. On en déduit qu'un tel triangle est équilatéral.

Il suffit, pour conclure de montrer qu'il existe au moins une solution.

  • Il existe une solution au problème isopérimétrique dans le cas des triangles :
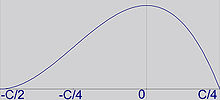
Problème-isopérimétrique-maximum.jpg

Il faut montrer qu'il existe un triangle de périmètre p et d'aire maximale. Le lemme montre qu'il existe un triangle isocèle Ti de périmètre p et d'aire plus grande que celle du triangle initial. Il suffit donc de montrer que tout triangle isocèle de périmètre p est d'aire plus petite que celle d'un triangle Te de périmètre p et de côté c. Soit c + 2ε la longueur de la base de Ti et c - ε la longueur des deux cotés égaux. Ici ε est un nombre réel compris entre -c /2 et c /4. La surface de Ti est le produit de la mi-longueur 1/2(c + 2ε) par la hauteur h, donnée par le théorème de Pythagore :

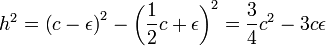
h^2 = \left(c - \epsilon\right)^2 - \left(\frac 12 c + \epsilon\right)^2= \frac 34c^2 - 3 c\epsilon

Si ai est l'aire du triangle isocèle, on dispose de la formule :

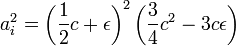
a_i^2 = \left(\frac 12 c + \epsilon\right)^2 \left(\frac 34c^2 - 3 c\epsilon\right)

La fonction, qui à ε associe ai2 est continue, elle est illustrée sur la figure de droite. En effet, c'est un polynôme du troisième degré. Elle est définie sur un segment, le théorème des bornes nous assure que le maximum est atteint. C'est-à-dire qu'il existe au moins une solution au problème isopérimétrique pour les triangles. Graphiquement, on remarque que celle solution correspond au point ε = 0, c'est-à-dire au triangle équilatéral. Ce résultat concorde avec la proposition précédente.

 

Exemples

Les remparts d'une ville

L'enceinte d'une ville du moyen-âge se rapproche souvent d'un cercle. Celle de Paris, à l'époque de Philippe Auguste n'en est pas très éloignée.
La ville de Cologne applique le principe isopérimétrique à la manière de Didon. La géométrie n'est pas celle d'un plan, mais un demi-plan.

Didon n'est pas la seule dirigeante à être confrontée à la question de la plus grande surface pour un périmètre donné. Les remparts d'une ville du Moyen-Âge demandent à la fois un gros travail de construction et une soldatesque abondante pour protéger la ville en cas d'attaque. Ces deux raisons favorisent de maximiser la surface intérieure de la ville par rapport à son périmètre.[20]

La géométrie utilisée n'est pas toujours celle du plan euclidien. Un demi plan euclidien permet par exemple d'obtenir un meilleur rapport. La solution est le demi cercle, elle est deux fois plus efficace. À l'aide d'un rempart de longueur p, on couvre une surface de p2/2π. La ville de Cologne adopte cette approche pour protéger sa ville au Moyen-Âge.

Au XVIIIe siècle d'autres contraintes favorisent une géométrie très différente. Celle de Lille par exemple, est fondée sur le principe de la tenaille, présentant des arêtes difficile à canonner de face. Elle offre une meilleure résistance à une attaque par l'artillerie.

L'œil du bouillon

L'œil dans un bouillon est constitué par une goutte d'huile en suspension dans l'eau. La surface de contact entre l'huile et l'eau est consommatrice d'énergie potentielle. L'équilibre, atteint pour le point d'énergie potentiel la plus basse est obtenue par la géométrie minimisant cette zone d'interface. Pour parler en termes imagés : « Les molécules les plus mal à l’aise se trouvent à l’interface (c’est-à-dire entre l’huile et le bouillon) donc plus l’interface est grande, plus le système est mal à l’aise[21] ».

Pour cette raison, les gouttes adoptent une géométrie circulaire. Si deux yeux fusionnent, ils adoptent instantanément cette forme. Si un œil est coupé en deux, par exemple à l'aide d'un couteau, les deux yeux obtenus reprennent aussi une forme circulaire.

Cette même cause impose aux bulles de savon de taille pas trop vaste, une forme sphérique. L'énergie potentielle est maximale si la surface de la bulle est minimale, la bulle a tendance à enfermer le volume d'air dans un espace sphérique, car il minimise au mieux la surface, pour un volume donné (celui de l'air emprisonné).

L'icosaèdre

Article détaillé : Icosaèdre.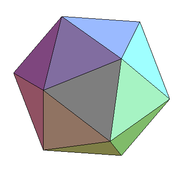
L'icosaèdre est le solide de Platon ayant le quotient isopérimétrique le plus élevé.

Le théorème d'isopérimétrie indique que, pour tout solide mesurable, de surface mesurable, le volume est plus petit que celui d'une sphère de même surface. Ainsi un solide de surface S possède toujours un volume V inférieur à Vs, celui d'une sphère de même surface :

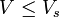
V \le V_s\;

La sphère de rayon r possède une surface de 4πr2, le rayon r de la sphère en question est égal à √S/2√π. Le volume Vs est égal à 4πr3/3. On en déduit une nouvelle majoration :

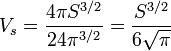
V_s = \frac {4\pi S^{3/2}}{24\pi^{3/2}} = \frac {S^{3/2}}{6\sqrt {\pi}}

La formule s'exprime plus simplement si elle est mise au carré, on obtient :

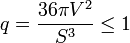
q = \frac {36\pi V^2}{S^3} \le 1 \;

Ce qui donne une forme d'inégalité isopérimétrique et la formule du quotient isopérimétrique, noté ici q. Dans le cas d'un icosaèdre, et si a désigne l'arête du solide, on dispose des formules suivantes :

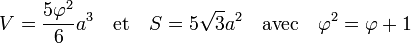
V = \frac{5\varphi^2}{6} a^3 \quad\text{et}\quad S = 5 \sqrt{3} a^2 \quad \text{avec}\quad \varphi^2 = \varphi + 1

Ici, φ désigne le nombre d'or égal à 1/2(1 + √5). On trouve :

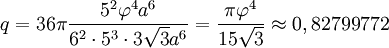
q = 36\pi\frac {5^2\varphi^4 a^6}{6^2\cdot 5^3\cdot 3\sqrt 3 a^6}= \frac {\pi\varphi^4}{15\sqrt 3} \approx 0,82799772

Ce quotient isopérimétrique est la valeur la plus élevée possible pour un solide de Platon.

Notes et Références

Notes

  1. ↑ Cette gravure date de 1630 et provient de l'Historische Chronica Frankfurt. Elle est l'œuvre de Mathias Merian l'Ancien.
  2. ↑ Virgile, Énéide [détail des éditions] [lire en ligne] Livre 1,16
  3. ↑ Cette information sur la longueur provient de Le problème isopérimétrique Irem d'Orléans p 1
  4. ↑ B. Teissier Volumes des corps convexes, géométrie et algèbre Institut de Mathématiques de Jussieu. Leçon donnée le jeudi 7 octobre 1999 Rédigée par C. Reydy p 2
  5. ↑ On trouve cette définition dans l'article F. Viot L'élaboration du calcul des variations et ses applications à la dynamique Mnémosyne N° 4-5. pp 35 63 (ISBN 2866120868)
  6. ↑ B. Teissier Volumes des corps convexes, géométrie et algèbre Institut de Mathématiques de Jussieu. Leçon donnée le jeudi 7 octobre 1999 Rédigée par C. Reydy p 2
  7. ↑ W. Dunham The Mathematical Universe: An Alphabetical Journey Through the Great Proofs, Problems, and Personalities Wiley (1997) p 112 (ISBN 0471176613)
  8. ↑ T. Heath A History of Greek Mathematics, Vol. 2 Dover Publications p 206 (1981) (ISBN 0486240746)
  9. ↑ P. Nahin When Least Is Best: How Mathematicians Discovered Many Clever Ways to Make Things as Small (or as Large) as Possible Princeton University Press p 47 (2007) (ISBN 0691130523)
  10. ↑ I. Thomas Greek Mathematical Works: Volume II, From Aristarchus to Pappus Loeb Classical Library p 395 (1941) (ISBN 0674993993)
  11. ↑ R. Lorch Abū Ja'far al-Khāzin on Isoperimetry and the Archimedean Tradition Zeitschrift für Geschichte der arabisch-islamischen Wissenschaften Vol. 3 pp. 150-229 (1986)
  12. ↑ H. Bellosta À propos de l’histoire des sciences arabes SMF Gazette Vol. 82 (1999)
  13. ↑ Cette information provient de : Le problème isopérimétrique Irem d'Orléans p 11
  14. ↑ B. Teissier Volumes des corps convexes, géométrie et algèbre Institut de Mathématiques de Jussieu. Leçon donnée le jeudi 7 octobre 1999 Rédigée par C. Reydy p 6
  15. ↑ Elle s'inspire d'une idée issue de : D. Wells Curious and Interesting Geometry, The Penguin Dictionary of Penguin (Non-Classics) (1992) p 123 (ISBN 0140118136)
  16. ↑ La preuve présentée ici est très classique, on la trouve par exemple dans : Le problème isopérimétrique Irem d'Orléans p 4
  17. ↑ On trouve la démonstration dans : Le problème isopérimétrique Irem d'Orléans p 7
  18. ↑ Cette démonstration est parfois présentée comme complète et rigoureuse : G. Villemin Calcul des variations Nombres : curiosités théorie usage. Les documents universitaires prennent une position opposée. B. Teissier place la première démonstration rigoureuse près de 60 ans plus tard : Volumes des corps convexes, géométrie et algèbre Institut de Mathématiques de Jussieu. Leçon donnée le jeudi 7 octobre 1999 Rédigée par C. Reydy p 6
  19. ↑ F. Dress Quelques grands problèmes en mathématiques Bulletin de la société mathématiques de France T 115 (1987) p 43
  20. ↑ Cet exemple est repris du site : Le problème isopérimétrique Irem d'Orléans p 1
  21. ↑ Le problème isopérimétrique Irem d'Orléans p 1

Liens externes

Références

  • (en) I. Chavel Isoperimetric Inequalities: Differential Geometric and Analytic Perspectives Cambridge University Press (2001) (ISBN 0521802679)
  • (en) D. Pollard A User's Guide to Measure Theoretic Probability Cambridge University Press (2001) (ISBN 0521002893)
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Isop%C3%A9rim%C3%A9trie ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Isoperimetrie de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Isopérimetrie — Isopérimétrie La forme d une bulle de savon est une réponse à une question d isopérimétrie. Sa géométrie est sphérique car c est le solide qui englobe le plus vaste volume dans une surface de mesure donnée. En géométrie plane, l isopérimétrie… …   Wikipédia en Français

  • Isopérimétrie — La forme d une bulle de savon est une réponse à une question d isopérimétrie : elle forme une sphère car c est le solide qui minimise la surface pour englober un volume donné, ce qui correspond au même problème de forme que de maximiser le… …   Wikipédia en Français

  • Isoperimetrie — Zur Isoperimetrie (Gleichheit des Umfanges) siehe Isoperimetrisches Problem Isoperimetrische Ungleichung Diese Seite ist eine Begriffsklärung zur Unterscheidung mehrerer mit demselben Wort bezeichneter Begriffe …   Deutsch Wikipedia

  • Isoperimetrie — Iso|pe|ri|me|trie* die; <zu ↑isoperimetrisch u. 2↑...ie> Gleichheit des Umfanges (Math.) …   Das große Fremdwörterbuch

  • Perimetre — Périmètre Le périmètre du carré vaut ici 8 …   Wikipédia en Français

  • Périmetre — Périmètre Le périmètre du carré vaut ici 8 …   Wikipédia en Français

  • Périmètre — Cet article de vulgarisation évite les aspects trop pointus ou techniques. Pour consulter un article plus détaillé, voir : Longueur d un arc. Le périmètre du carré vaut ici 8 …   Wikipédia en Français

  • ΠR — Périmètre Le périmètre du carré vaut ici 8 …   Wikipédia en Français

  • Theoreme isoperimetrique — Théorème isopérimétrique En géométrie, un théorème isopérimétrique traite d une question concernant les compacts d un espace métrique muni d une mesure. Un exemple simple est donné par les compacts d un plan euclidien. Les compacts concernés sont …   Wikipédia en Français

  • Théorème isopérimétrique — En géométrie, un théorème isopérimétrique traite d une question concernant les compacts d un espace métrique muni d une mesure. Un exemple simple est donné par les compacts d un plan euclidien. Les compacts concernés sont ceux de mesures finies… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”