- Viète
-
François Viète
François Viète 
d'après Daniel ou Jean Rabel Naissance 1540
Fontenay-le-Comte (France)Décès 23 février 1603
Paris (France)Nationalité Française Champs Algèbre,
Cryptographie
et Géométriemodifier 
François Viète, ou François Viette, en latin Franciscus Vieta, est un mathématicien français, né à Fontenay-le-Comte (Vendée) en 1540 et mort à Paris le 23 février 1603.
De famille bourgeoise et de formation juridique, il a été l'avocat de grandes familles protestantes, dont les Parthenay-l'Archevêque et les Rohan, avant de devenir conseiller au parlement de Rennes, sous Charles IX, puis maître des requêtes ordinaires de l'hôtel du roi sous Henri III. Maître des requêtes et Déchiffreur d'Henri IV, puis membre du petit conseil, il mena, parallèlement à ces charges au service de l'État, une carrière de mathématicien « amateur » qui le fit honorer de son vivant par les plus grands professionnels de son temps.
Inspiré par Ramus, Gosselin et Jacques Pelletier du Mans, il restaura la géométrie des anciens (Apollonius, Theon et Diophante) et prolongea les travaux d'Albategni, de Rheticus et de Regiomontanus sur les sinus et les triangles sphériques. La publication de son livre phare Isagoge Artem Analycitem ou Isagoge marque en 1591 le début de la révolution algébrique qui, poursuivie par Thomas Harriot, William Oughtred, Albert Girard et René Descartes, fondera les notations de l'algèbre contemporaine. Notant, pour la première fois dans l'histoire de l'humanité, les paramètres d'une équation par des symboles, il fonde ainsi l'algèbre nouvelle ou « logistique spécieuse », une version « homogène » à notre façon actuelle de mener les calculs symboliques. Écrivant en latin, et connu de toute l'Europe, il formera quelques élèves, Nathanael Tarporley, Pierre puis Jacques Aleaume, Marino Ghetaldi, Jean de Beaugrand, Alexander Anderson, et des correspondants dont Lansberg de Meulabeecke, qui contribueront à sa renommée et prolongeront ses méthodes, les diffusant en Angleterre, en Hollande, en Italie et en Allemagne. Il eut aussi quelques contradicteurs, Adriaan Van Roomen, Joseph Juste Scaliger, dont il triompha.
Une partie de ses travaux est dédiée à l'astronomie. Mais il ne publia pas sa découverte de la forme elliptique des orbites des planètes, qu'il découvrit plus d'une décennie avant Johann Kepler. Apprécié par Pierre de Fermat, Huyghens, et Newton, sa « logistique spécieuse » fut la façon d'écrire des mathématiques jusqu'à la suppression des contraintes d'homogénéité par Descartes et la réédition que Van Schooten fit de ces ouvrages. Les mathématiciens du XIXe siècle, Michel Chasles et Joseph Bertrand[1] redécouvriront sa figure et l'importance de ses travaux, notamment ceux qui préfiguraient l'invention du triangle sphérique polaire et celle des inversions. Enfin, par ses travaux de déchiffreur, et singulièrement les dernières recommandations qu'il communiqua au duc de Rosny quelques semaines avant sa mort, François Viète fut l'un des premiers cryptologues à donner de solides indications sur l'art de casser les codes.
Biographie
Origines
Son grand-père, qui lui-même se nomme François Viette, est un marchand originaire de la Rochelle ; celui-ci s'installe dans la paroisse de Foussais-Payré[2]. Il fait donner une solide instruction à ses fils[3] : Mathurin, Jean, et Étienne. Il a aussi deux filles, Jeanne et Josèphe. Le second de ses fils, Étienne Viète, le premier à écrire son nom avec un seul t[4], devient procureur de Fontenay-le-Comte[5] et notaire de Busseau. Épousant Marguerite, fille de François Dupont et de Françoise Brisson, Étienne se lie à la famille de Barnabé Brisson, futur premier président du parlement de Paris et pendu pendant la domination de la Ligue[6] ; habitant de 1535 à 1547, au 34 grand rue, où est probablement né le mathématicien[7] (du temps de Benjamin Fillon[8], entre la rue Perate et la rue des trois rois), le couple emménage par la suite une maison située à l’emplacement des actuels 2 rue du Puy de la Vau et 32 rue Gaston Guillemet. Étienne Viète reçoit en héritage la métairie de la Bigotière. Sept enfants, trois garçons et quatre filles, naissent de son union avec Marguerite Dupont. François, qui est l'aîné, Nicolas, René, ainsi que Claude, Françoise, Jeanne, et Julie (ou Julienne)[9]
En ancien poitevin, Viette signifie « rusé[7]. »
Quoique catholique[7], la famille se montre sensible aux idées de la réforme. Néanmoins, si Étienne se convertit à la nouvelle foi, Nicolas et René demeurent fidèles à Rome. Un fils de Mathurin, prénommé également François, fera bientôt profession de calvinisme[10],[7]. Ces territoires du bas-Poitou sont en effet soumis à l'influence des seigneurs huguenots d'Aubeterre, du Pons et de Parthenay, qui depuis le retour de Ferrare de Michelle de Saubonne, professent la nouvelle doctrine et font dire le prêche sur leurs terres. Dans sa jeunesse, Viète est sans doute l'élève des franciscains, au collège des Cordeliers, dans le collège où a vécu François Rabelais[3]. On connaît également de lui une dissertation, lue devant un précepteur, Evrardus Bellona, en 1555[7], et publiée dans Quinque orationes philosophicae sous le nom de Franciscus Vietoe. Ses autres camarades sont : Franciscus Talpinus, Tusseanus Puteanus, Franciscus Raguellus et Franciscus Morellus. Le titre de sa dissertation est Quod Captae ab hostibus regionis melior est quam vastata conditio.
À partir de 1555, il fréquente la faculté de droit de Poitiers, dont il sort bachelier et licencié ès droit en 1559[11]. Il y a pour coreligionnaire Charles Tiraqueau, petit fils du poète André Tiraqueau Pierre Gabryaud, Nicolas Rappin[12] et Scevole de Sainte-Marthe. En 1560, il devient avocat au barreau de Fontenay-le-Comte et réside dans un petit hôtel à Fontenay, qu'il possède en héritage, mais on le nomme déjà Sieur de la Bigotière sur les actes d'état civil[3] (néanmoins, cette terre est indivise avec ses frères et il ne leur rachètera leurs droits qu'en 1564 pour René, 1574 pour Nicolas[3]). Fondé de pouvoir de son père à Paris (acte du 26 août 1560[3]), on lui confie alors des affaires importantes, notamment un partage de revenus ecclésiastiques à la Rochelle (acte du 15 février 1561), la liquidation des fermages en Poitou de la veuve de François Ier(acte introuvable selon la thèse de J. Grisard[7]) ou encore les intérêts de Marie Stuart, reine d’Écosse[13], pour sa part d'un trésor qu'un laboureur a trouvé sur ses terres et dont le partage donne lieu à procès (acte du 21 janvier 1564).
Au service des Parthenay
 Blasonnement : burelé d'argent et d'azur, à la bande de gueules brochant sur le tout. Ces armes étaient celles des seigneurs de Parthenay.
Blasonnement : burelé d'argent et d'azur, à la bande de gueules brochant sur le tout. Ces armes étaient celles des seigneurs de Parthenay.
En 1564, à la suite de son oncle Brisson, il entre au service d’Antoinette d'Aubeterre, épouse de Jean de Parthenay-l’Archevêque, dit Soubise, un des plus grands capitaines de guerre calvinistes[3]. Elle le fait venir dans sa résidence du Parc-Mouchamps, aux Herbiers, comme secrétaire particulier chargé de défendre les intérêts de sa famille[14].
Jean V de Parthenay, adversaire du duc de Guise et seigneur de Soubise, a tenu la ville de Lyon (jusqu'en 1563) sur ordre du prince de Condé, un des fils de Jeanne d'Albret. Défendant cette ville contre les armées royales commandées par le duc de Nemours, il n'en a rendu les clefs au roi qu'après la signature de la paix d'Amboise. Or, pendant sa défense de Lyon, le duc de Guise a été assassiné par un des lieutenants des Parthenay, Poltrot de Méré. Soumis à la torture, ce dernier accusa l'amiral Coligny, Théodore de Bèze et Jean de Parthenay d'avoir commandité le meurtre.
Par suite, une des missions dont Antoinette d'Aubeterre charge François Viète est d'assurer la défense de son époux. À cette fin, il axe sa plaidoirie sur la conduite exemplaire des armées de Jean V de Parthenay à Lyon, et le suit dans cette ville, lors du passage de la cour (juin 1564), afin de recueillir les faits relatifs au siège que Soubise a soutenu l’année précédente contre les armées de Nemours pendant qu'ils étaient dans toutes les mémoires[15].
Étant parvenu à innocenter Soubise des accusations portées contre lui par la maison de Guise, François Viète revient au parc-Soubise, à Mouchamps et reprend sa place de secrétaire. Généalogiste de la famille, il en retrace l'histoire depuis les origines des Lusignans et, vers 1565, devient le précepteur de la fille de Soubise, Catherine de Parthenay, alors âgée de onze ans[3]. Comme ses pères et mères, la jeune fille connaît déjà le latin, le grec et l'hébreu, François Viète lui enseigne les sciences, et notamment des rudiments d'astronomie, de géographie et de trigonométrie. Femme d’action, de lettres et de sciences, elle entretiendra par la suite avec lui une relation mutuellement admirative, qui ne faiblira jamais et ne s'éteindra qu'à la mort de Viète, en 1603. Pour elle, à fins éducatives, il rédige de nombreux traités, dont un seul, traitant de principes de cosmographie, nous est parvenu[16]. Traduit en français, ce traité, publié plusieurs fois entre 1641 et 1647, donne de précieuses indications sur les conceptions astronomiques dominantes dans ce foyer huguenot.
Pour elle, il écrira un jour, en préface de son œuvre principale :
« C'est à vous, auguste fille de Mélusine, que je dois mes études mathématiques, auxquelles m'a poussé votre amour pour cette science[10]. »À cette époque, Jean V de Parthenay le présente au roi Charles IX[14], mais après un an passé en pourparlers avec Catherine de Médicis, Soubise meurt (le 1er septembre 1566). Viète rédige alors sa biographie, intitulée Mémoires de la vie de Jean de Parthenay-Larchevêque, sieur de Soubise, (publiée pour la première fois en 1879 par J. Bonnet)[17]. Celle-ci sera plusieurs fois remaniée (notamment en collaboration avec Catherine de Parthenay)[18].
La question de l'adhésion de Viète à la foi protestante lorsqu'il vivait au parc Mouchamps semblait acquise jusqu'aux travaux de Benjamin Fillon et de Frédéric Ritter. Élevé dans la foi catholique, et en faisant toujours profession dix ans plus tard, leur thèse est que sa conversion, si conversion il y eut, fut de courte durée et peu profonde[3]. Effectivement, dans son traité de cosmographie, François Viète, s'il fait allusion au « Créateur », ne mentionne jamais selon quel mode on doit lui rendre grâce. Il semble que, dès cette époque, il suive les traces de Michel de l'Hospital et du parti des politiques (Frédéric Ritter le croit indifférent en matière religieuse, Grisard est plus mesuré sur ce point).
Entre temps, François Viète s'est marié avec Barbe Cothereau, fille de Jehan Cothereau, marchand de Luçon, et petite-fille de dame Garotine (actes du 17 juin 1566 et du 29 janvier 1586)[7],[19].
À la Rochelle
Dans l'année qui suivit la mort de Jean V de Parthenay, Antoinette d'Aubeterre se met en quête d'un parti pour sa fille. Parmi les trois prétendants, Châtillon (le fils de l'amiral de Coligny, qui meurt entre temps), René de Rohan (qui n'est pas assez titré) et Charles de Quellenec, baron du Pont, elle choisit ce dernier et trouve ainsi un protecteur aux terres des Parthenay[3]. Mais le baron Charles de Quellenec, après avoir épousé Catherine de Parthenay le 15 juin 1568, se montre vite un gendre indocile. Déçue de ne pouvoir régner sur le parc Soubise comme au temps de son époux, la dame d'Aubeterre s'exile en septembre 1568 à la Rochelle, où elle rejoint la cour de Jeanne d'Albret. François Viète la suit[20], et rencontre dans son sillage la très haute aristocratie calviniste : les principaux chefs militaires, Coligny et Condé, mais aussi Jeanne d’Albret, reine de Navarre et le fils de celle-ci, Henri de Navarre, le futur Henri IV[21], et encore Françoise de Rohan, qui bientôt va l'employer dans ses fameux procès.
Après avoir combattu sous les ordres de René II de Rohan en Saintonge, le baron de Quellenec qui a relevé le nom de Soubise, est défait à la bataille de Jarnac. Fait prisonnier, il s'évade et rejoint Mouchamps. Cependant, il se révèle bien vite incapable de donner une descendance aux Parthenay. Des confidences de domestiques alertent Antoinette d'Aubeterre et bientôt, en septembre 1570, sa fille vient se réfugier auprès d'elle. L'affaire vient devant Jeanne d'Albret et Théodore de Bèze conseille de rompre le mariage. En réaction, De Quellenec vient rechercher son épouse à la Rochelle et l'enferme dans son château breton. Pour correspondre avec sa mère, celle-ci insère alors quelques vers de langue non connue (par son mari) dans les lettres qu'elle envoie vers la Rochelle et fait connaître à son ancien précepteur qu'elle a écrit entre les lignes, au jus d'orange, des caractères qui se révèlent lorsqu'on les approche d'un flamme[22],[7]. Ceci est le premier témoignage sur le rapport de Viète avec le déchiffrement de lettres secrètes. Après d'autres récriminations auprès de Jeanne d'Albret et Théodore de Bèze, Antoinette d'Aubeterre, convaincue de l'inanité de son gendre, finit par intenter un procès au baron de Quellenec (le 11 septembre 1571) devant le parlement de Paris.
Vers cette époque, François Viète refuse de lui servir d'avocat contre le baron de Quellenec[14], quitte son service et se déplace à Paris (où Ritter le croit avocat mais J. Mangis[23] n'en trouve aucune trace). Sans doute peut-il compter sur son oncle Barnabé Brisson, ainsi que sur l'appui de ses amis et clients protestants, pour se faire un nom dans la magistrature. Par ailleurs, il a déjà rédigé une grand partie de son Canon mathématique[3] et le propose à l'éditeur Mettayer en 1571.
Les débuts à Paris
Domicilié à Paris, Viète continue néanmoins à visiter son élève et à rallier régulièrement Fontenay-le-Comte, où il occupe des fonctions municipales[6]. D'après le témoignage de Jacques-Auguste de Thou, il poursuit ses recherches mathématiques la nuit ou pendant des périodes de loisir. Il a la réputation de demeurer près de trois jours sur une question, le coude sur la table de travail et de s’y nourrir sans changer de position (selon de Thou)[24]. On pense que dès cette époque, il fut en rapport avec Ramus, Gosselin et Jacques Pelletier du Mans. Néanmoins on ne dispose d'aucune certitude sur ce fait. Frédéric Ritter, son biographe du XIXe siècle croit pouvoir affirmer qu'il a déjà pris en mains les intérêts de Françoise de Rohan.
En 1572, Catherine de Parthenay, Françoise de Rohan et son frère René viennent à Paris pour assister au mariage du roi de Navarre et de la Reine Margot. Ils parviennent par chance à s'enfuir de la capitale à l'aube de la Saint-Barthélemy. Prévenus par anonymement[3], ils franchissent les portes avant le début du massacre. François Viète est probablement à Paris cette nuit-là ; nuit pendant laquelle le baron de Quellenec est assassiné dans la cour du Louvre quelques heures après l'assassinat de l'amiral Coligny[25],[26],[27] [28],[29]. Ramus périt également peu après cette nuit-là. Son cadavre est traîné par une foule d'étudiants et promené d'université en université en hommage à Aristote.
Lié avec Françoise de Rohan (avec laquelle Benjamin Fillon soutint qu'il eut une aventure[6]) qui se prétend toujours duchesse de Nemours, mais plus connue sous le nom de dame de la Garnache, il l'accompagne à Beauvoir-sur-Mer (acte du 26 décembre 1572) et la soutient dans le procès qu'elle nourrit contre le duc de Nemours[30],[31]. Il se met également au service des intérêts de son frère, René II de Rohan et semble jouer le rôle d'un puissant auxiliaire[32] pour triompher de la résistance de la dame de Soubise (Antoinette d'Aubeterre) au mariage de Catherine de Parthenay et du futur duc de Rohan[33]qui possède par ailleurs une maison de ville à Beauvoir surnommée l'Ardouinière, dans la rue qui va de la halle au château[7]. Alors que Françoise de Rohan (sa sœur) subit les persécutions des troupes royales, dirigées par Mercœur, René de Rohan combat le duc de Montpensier à Lusignan, où il s'enferme et mène une résistance héroïque (il ne capitulera qu'en février 1575). Catherine de Parthenay fait jouer sa tragédie Holopherne dans La Rochelle assiégée.
En 1573, après la levée du siège de La Rochelle et la rentrée en grâce des chefs protestants, François Viète est nommé par Charles IX conseiller au parlement de Rennes (24 octobre 1573). Cette charge de conseiller est parmi les moins onéreuses, notamment pour les conseillers issus du Poitou[3], de plus elle n'est guère contraignante, le parlement ne siégeant qu'une fois l'an d'août à octobre[34]. Pour y être agréé, Viète doit y témoigner de sa foi catholique, le 6 avril de l'année suivante en une cérémonie dont les minutes sont conservées dans les archives secrètes de ce parlement[35],[7].
L'acte qui nomme Viète est libellé ainsi :
« Charles par la grâce de Dieu, roy de France, à tous ceux qui la présente verront, salut. Savoir faisons que nous a pleine confiance de la personne de notre cher et amé Maître François Viette, avocat à la court de Parlement de Paris et de ses sens suffisance, littérature, loyauté, prudhommie, expérience en fait de judicature et bonne diligence... avons donné et octroyé, donnons et octroyons, par ces patentes l'état et office de Conseiller à la Court du Parlement de Bretagne...[10] »Le 16 mai 1575, le duc Henri de Rohan, dit Henri le goutteux, meurt au château de Blain ; sa fille, de douze ans, meurt quelques jours après lui[3]. Dernier frère d'Henri, (leur autre frère, Jean, est mort sans descendance mâle), René de Rohan devient duc à son tour. Antoinette d'Aubeterre accepte dès lors le remariage de l'hériitière des Parthenay avec le frère de la dame de la Garnache[33], mariage qui a lieu le 25 avril de la même année.
Maître des requêtes
En 1576, probablement sur recommandation de Françoise et de René de Rohan, François Viète entre au service du roi Henri III, comme chargé de mission spéciale. Sa présence au parlement de Rennes durant la session annuelle s'en ressent fortement : si les deux premières années de sa charge, il assiste à de nombreuses séances du parlement, il ne siège plus dans la Cour de Rennes ni cette année-là, ni la suivante. Il est excusé par le roi, qui lui fait néanmoins tenir ses gages [6]. Le roi affirme dans des lettres patentes :
« Nous avons advisé d'employer notre ami et féal conseiller en notre cour, Maître François Viète, Seigneur de la Bigotière ; nous l'avons donc fait venir en notre cour et suite, en laquelle il était nécessaire qu'il fasse quelque séjour et même durant les mois d'août, septembre et octobre prochain. Nous lui avons permis et permettons qu'il lui soit loisible désemparer d'icelle notre cour durant la séance des dits trois mois... »L'hiver 1577, il réside à Beauvoir-sur-Mer, près de la dame de la Garnache. Parallèlement, il agrandit sa maison de Fontenay (acte du 8 novembre). Le fils que celle-ci a eu avec le duc de Nemours, venant d'Allemagne avec quelques routiers, est capturé cette année-là par le duc de Montpensier. Il échappe à la potence, par l'action du Roi ; mais le duc refuse de le rendre, même contre rançon[3].
En 1578, François Viète paraît six jours en août, trois en septembre et cinq en octobre devant le parlement de Rennes. Son absence lors de la messe du Saint Esprit est très remarquée. L'année suivante, il ne paraît que le 15 octobre pour s'excuser de ses absences[7]
De toutes les missions, extraordinaires et secrètes que lui confie Henri III à cette époque, une seule sera divulguée pour apaiser la colère de ce parlement et concerne la vente de bois du domaine royal[3]. Peu de choses de cette période de la vie de François Viète sont connues mais aux dires de son éditeur Jamet Mettayer, on peut juger qu'il est entièrement occupé par le service de l'État. Ayant pénétré fort avant dans la confiance d'Henri III, Viète suit une Cour qui, selon le mot d'Armand Baschet décrivant la vie quotidienne des derniers Valois, ne réside pas mais campe. Viète trouve néanmoins le temps pendant cette période de visiter Catherine de Parthenay dans ses châteaux bretons de Salles et de Blain[3] et de presser les imprimeurs pour hâter l'impression de son premier ouvrage mathématique.
En 1579, celui-ci sort enfin des presses de l'éditeur Jamet Mettayer. Mais après 8 ans de travail, François Viète est fort mécontent de l'impression de son Canon mathématique et particulièrement des compléments qui figurent à la suite de cet ouvrage. Ce livre, Des inspections mathématiques, donne les sinus à l'aide de formules et marque un premier pas dans la création du formalisme algébrique. Le livre étant truffé d'erreurs, Viète menace d'en faire détruire tous les exemplaires. C'est pourtant dans ce livre qu'il donne par la méthode d'Archimède et à l'aide d'un polygone à 393 216 côtés (6×216) un encadrement rigoureux de π avec onze chiffres exacts, valeur notée à l'aide de nombres décimaux, dont il est l'un des premiers à montrer l'utilité, sinon le créateur[6].
Vers la même époque à l'occasion de la paix de Flers, le duc d'Alençon et Viète obtiennent le règlement du procès opposant le duc de Nemours à Françoise de Rohan, au bénéfice de cette dernière. Les lettres royales datent du 16 novembre 1579. Elles mettent la dame de la Garnache sous la protection d'Henri III, qui écrit :
- Nous entendons et ordonnons qu'il ne puisse lui être fait aucun blâme pour raison de ce qui est advenu et nous la déclarons libre de contracter mariage[3].
Sa terre du Loudunois élevé en duché, la libération de son fils, 20 000 écus pour celui-ci et l'assurance d'en toucher 50 000 pour la dame de la Garnache mettent un terme à ce procès qui a duré plus de vingt ans. La conclusion de cette affaire, très favorable à Françoise de Rohan, vaut vraisemblablement à Viète la rancune tenace du parti ligueur[32]. Ces lettres patentes seront néanmoins contresignées par le parlement de Paris et la cour des comptes en 1582.
Toujours en 1580, son oncle Barnabé Brisson achète la charge de président à Mortier du parlement de Paris et le 25 mars de la même année[7], François Viète est autorisé à se défaire de sa charge au Parlement de Bretagne : Henri III le nomme maître des requêtes au parlement de Paris, attaché au service exclusif du roi.
A cette époque, les conseillers ordinaires habitent les logis royaux et reçoivent les requêtes des parties pour les mettre sous les yeux du roi. Reçus et examinés par le Parlement de Paris, ils ont rang de conseillers et prennent place immédiatement après le président, avec autorité et voix de délibération sur toutes les affaires du royaume. Ils passent toutefois une grande partie de leur temps à cheval, mandaté par le roi, pour régler telle ou telle affaire urgente dans les provinces, récolter de l'argent, calmer les parlements, acheter des soutiens. Ce sont de véritables missi dominici. Un privilège de poste leur assure des facilités pour obtenir des chevaux frais. Ils ne sont pas récompensés en épices mais en frais de mission[36], ils ont interdiction de se mêler d'autres affaires que celles du Roy sans son autorisation expresse et dérogation aux ordonnances.
L'année qui suit, Viète doit épauler la dame de la Garnache dans deux affaires, l'une qui l'oppose au poète Nicolas Rapin, alors en charge de la prévôté de Fontenay-le-Comte, ligueur convaincu à cette époque, qui la menace par ce qu'elle protège la religion reformée[6] ; l'autre concernant le fils qu'elle a eu du duc de Nemours, qui se prétend toujours duc de Genevoix et qui, meurtrier d'un orfèvre à Paris et ayant résisté aux forces de police venues l'arrêter, sera enfermé au Châtelet (jusqu'au 15 janvier 1585). Deux affaires sordides, qui réclament toutes deux l'intervention du roi de Navarre. De juin à juillet 1581, Viète agrandit de nouveau son hôtel de Fontenay[3].
L’exil studieux dans le Poitou
En 1583, Françoise de Rohan accueille dans son château Dom Anthonio, héritier de la maison de Portugal, dépossédé de son royaume par Philippe II. Le roi de France l'arme pour une seconde expédition (malheureuse) aux Açores. Le 3 novembre 1584, Viète vend à son cousin homonyme sa maison de Beauvoir-sur-Mer. Celui-ci devient receveur des fermes de la dame de la Garnache. Viète demeure alors au château de Françoise de Rohan.
Au premiers jours de 1585, la Ligue obtient la mise à l’écart des conseillers d'Henri III accusés de sympathie pour la cause protestante et le roi doit se séparer de François Viète entre janvier et février. Celui-ci se réfugie probablement à Beauvoir-sur-Mer, chez Françoise de Rohan. Henri de Navarre, qui est le neveu de la dame de la Garnache, écrit deux lettres en faveur du protégé des Rohan, afin d'obtenir son retour au service du roi, mais il ne sera pas écouté. Dans une lettre, datée de Montauban, le 3 mars 1585, le roi de Navarre écrit[37] :
« II y a quelque temps, qu’à la considération et prière très humble de mon oncle de Rohan et de ma tante la duchesse de Lodunnois, sa sœur, il vous pleust accorder un estat de conseiller et maistre des requestes ordinaire à monsieur François Viette, de l'exercice duquel il a esté discontinué par des considérations que Vostre Majesté pourra entendre. Et d'aultant, Monseigneur, oultre que le dict Viette est personnage très capable, Je l'ay tousjours connu si affectionné aux affaires de mon dict oncle que je supplie très humblement Vostre dicte Majesté, que le dict Vielle soit remis à l'exercice de son dict estat. »Une seconde lettre, datée de Bergerac, le 26 avril, n’a pas plus d'effet[10].
François Viète se retire donc dans le Poitou. Entre Fontenay et Beauvoir-sur-Mer, chez lui ou sur les terres de ses amies. Le 19 juin, le duc de Nemours meurt de la goutte, déliant définitivement la dame de la Garnache de ses vœux. À la fin de l'année 1585, René de Rohan meurt à l'âge de 36 ans et Catherine de Parthenay, veuve pour la seconde fois, quitte son château de Blain, en Bretagne, et se retire au parc-Soubise avec ses cinq enfants. Le mathématicien anglais Nathanael Tarporley[38], futur élève et ami d’Harriot, occupe probablement un poste de secrétaire (amanuensis) auprès de François Viète [39] pendant ces années-là et pour une période de deux à trois ans[40].
- ...the rather, now, because i am an gathering up my ruined wittes, écrit Tarproley à Harriot, the better to encounter that french Apollon, if it fortune that either his continue or my bouldness effects over conference ; tomorow being the day when i am appointed by his printer...[7]
Le 16 mars 1586, Viète afferme pour cinq ans sa métairie de la Bigotière, mais la même année, le 9 août, Françoise de Rohan, dont le château est investi par les troupes du duc de Mercœur contracte une promesse de mariage avec le capitaine François de Lefesle, chevalier de l'ordre du Roi et seigneur de Guébriand, dont on pense qu'il est chargé de commander la garnison catholique occupant le château de Beauvoir et qui l'abandonnera pour attaquer le château de Blain[41][42]. Henri III s'opposera à cette mésalliance[3] .
Fin 1586, Françoise de Rohan fait lever sur ses terres la taille royale par le cousin homonyme du mathématicien, François Viette, Sieur de Saint Nicolas.[7] L'année suivante, son fils, le turbulent duc de Genevoix assiège la Garnache, puis Beauvoir et elle supplie Catherine de Médicis de lui envoyer des renforts. Elle n'en reçoit qu'une lettre indignée (en date du 19 février 1587) lui demandant de rembourser la taille royale injustement confisquée. Elle s'enfuit alors à Nantes. Il lui faudra attendre que les troupes du roi Henri IV pacifient le Poitou pour retrouver ses places fortes. Frédéric Ritter affirme que Viète retourne alors sur Fontenay, reconquise en 1587 par les troupes du roi de Navarre. Le mathématicien retrouve son ancienne élève, Catherine de Parthenay, au parc-Mouchamps. Quoique l'époque soit bouleversée, il parvient, pendant ces quatre années de retraite à consacrer une grande partie de son temps aux mathématiques, rédigeant le programme qu’il fixe à l’Art Analytique (analyse spécieuse) ou Algèbre nouvelle et avançant sans doute dans la rédaction de ses Zététiques.
Les liasses de déchiffrements conservées entre 1588 et 1594 dans les cinq cents de Colbert font alors mention de son nom comme déchiffreur d'Henri III, puis d'Henri IV[3].
Déchiffreur de deux rois
Le 12 mai 1588, le roi Henri III est chassé de Paris par la journée des barricades. La cour se réfugie à Chartres, puis, devant l'avancée des troupes des ligueurs, à Blois. Viète reprend son office de maître des requêtes vers l'époque où le roi fait assassiner le duc Henri de Guise[3]. Henri III enjoint alors aux officiers royaux de se trouver à Tours avant le 15 avril 1589. Viète semble l'un des premiers à répondre à cet appel. Logé rue Traversayne dans un petit hôtel loué par les soins de l'éditeur, Jamet Mettayer qui a lui aussi suivi la cour, il y retrouve Pierre Aleaume d'Orléans, qui devient son secrétaire. On connaît le nom d'un de ses valets, Henri Garaud, qu'il emploie dans ses transactions avec ses frères[3], Nicolas et René, ses frères, demeurés à Fontenay et y occupant des positions en vue.
Alors que Viète, demeuré à Tours, déchiffre les dépêches codées des ligueurs et des ennemis du roi[43], Henri III est assassiné à Saint-Cloud par le moine Jacques Clément. Ce sera l'occasion pour Viète de commettre quelques vers latins inédits encore aujourd'hui, insinueux et grivois[3] contre le duc de Mercoeur et sa sœur, la duchesse de Montpensier, soupçonnés d'être les instigateurs de l'assassinat. Parallèlement, il commence la publication de son Isagoge.
Après la mort d’Henri III, Viète entre au conseil privé d’Henri IV (Grisard doute qu'il fit partie des douze membres du conseil restreint, car la liste qu'en donne Lavisse ne comporte pas son nom[44]). Il est cependant très apprécié du roi, qui admire ses talents mathématiques. En septembre 1589, usant d'analyse statistique et de méthodes qu'il se garde bien de publier, François Viète parvient à casser les codes[45] des lettres secrètes espagnoles[46]. Ceux-ci employaient une méthode par substitution [47], comportant de multiples symboles pour noter la même lettre et parfois des symboles nuls, une cinquantaine par lettre, tirés au sort parmi six cents caractères. Le 19 décembre 1589, il fait une apparition à Fontenay, pour la mort de son oncle Nicolas Dupont. La preuve que sa mère est encore en vie est apportée en cette occasion et sa signature apparaît sur un contrat passé par son frère Nicolas. En 1590, Henri IV l'autorise à rendre publique la lettre du commandeur Moreo au roi d'Espagne[48] qu'il a déchiffrée six mois plus tôt. Le contenu des lettres décodées par Viète, révèle que le chef de la Ligue en France, le duc de Mayenne, projette de devenir roi à la place d’Henri IV. Cette publication met le duc de Mayenne en position délicate et trouble beaucoup les Espagnols pendant deux ans. Ceux-ci conservent néanmoins leur méthode, persuadés qu'elle n'est pas réellement déchiffrable. Ritter pense que cette publication a favorisé le règlement des guerres de religion[10].
Le premier avril de cette même année, François Viète s'entremet auprès du roi Henri pour obtenir aide et soutient en faveur de la Dame de la Garnache contre les exactions des troupes de Mercœur. Le roi la confirme dans ses titres de duchesse de Loudunois et les troupes royales lui permettent de réintégrer ses châteaux. Dans une même lettre, il informe le roi de l'arrestation de deux porteurs de messages, Chamin et Perrin, qui ont trahi sa confiance et qu'il fait traduire devant le procureur du roi afin qu'il soit procédé contre eux criminellement[7].
En 1591, paraît chez Jamet Mettayer, l'ouvrage qui va bouleverser l'algèbre : In Artem Analycitem Isagoge. Cet opuscule est en quelque sorte l'acte de fondation de l'algèbre moderne. Dans sa dédicace à Catherine de Parthenay et à François de Rohan, il en fait le programme d'un art nouveau, entièrement restauré. Pour lui, cette façon de poser les problèmes géométriques doit conduire à la solution de tous les problèmes[10]. Cette publication sera immédiatement suivie par celle des cinq livres de Zététiques. En décembre de la même, Françoise de Rohan meurt à Beauvoir sur Mer.
Les traductions des messages secrets reçus à Tours se multiplient et Viète doit s'adjoindre Charles du Lys, un chevalier descendant de la famille de Jeanne d'Arc (par son frère) pour préparer la transcription de ces messages. On compte plus d'une dizaine de liasses de messages par mois, dont certains lui parviennent sans avoir été ouverts. Ils portent essentiellement sur les affaires espagnoles et les prétentions que le roi d'Espagne nourrit de marier sa fille avec le duc des deux ponts ou quelque prince de sang proche du trône pour proposer l'infante à la succession des Valois. On y trouve encore d'autres lettres, émanant de la ligue, du duc de Mayenne, du légat du pape ou des ambassadeurs vénitiens[3].
En 1592, Viète, quoiqu'en conflit avec son propriétaire, l'érudit Nicolas de Nancel, renouvelle son bail, à Tours, et agrandit son logis. Son travail de maître de requêtes se poursuit parallèlement à son emploi de déchiffreur[49]. En 1593, Catherine de Parthenay le retrouve dans cette ville, où elle donne un bal à l'occasion du retour d'exil de la reine Margot[3], le bal de Madame, qui mêle cavaliers français et béarnais. Cette année-là marque également le début de sa polémique avec l'humaniste protestant Joseph Juste Scaliger. Celui-ci, qui s'est fait un nom dans les lettres à la suite de son père et se réclame de la noblesse italienne sous le nom de Scala, se vante d'avoir résolu le problème de la quadrature du cercle, prétention vaine, qui a déjà couvert de ridicule des mathématiciens plus fameux (dont quarante ans auparavant, Oronce Fine). Viète en triomphe à de nombreuses reprises les deux années qui suivent[14],[24].
À partir de 1594, le mathématicien est chargé exclusivement du déchiffrage des codes secrets ennemis. Dans deux des lettres de François Viète à Henri IV[50] le mathématicien s'y déclare explicitement interprète et déchiffreur du Roy. À cette époque, il se lie d'amitié avec le conseiller Jean d'Espagnet[51]. Par les confessions de Dominique Baudier à Scaliger, on sait aussi qu'il mène grand train à Tours[7]. Enfin lors d'un dîner copieux, il semble qu'il se soit vanté devant les ambassadeurs vénitiens de déchiffrer leurs lettres et celles des espagnols depuis plus de deux ans[52]. Le roi d'Espagne l'apprend et accuse devant le pape, le roi de France d'user de magie[53] et Viète d'être un nécromant[24],[16]. Cette prétention fait rire toute la cour de France.
La polémique avec Scaliger
Joseph Juste Scaliger, après avoir affirmé qu'il tient la quadrature du cercle, publie entre 1592 et 1595 plusieurs poèmes et livres de cyclométrie destinés à étayer sa thèse. Remplis de considérations littéraires, ces ouvrages[54],[55] révèlent la totale incompétence[6] de l'érudit en matières mathématiques. Il y affirme entre autres
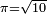 approximation très mauvaise, dont il croit détenir la paternité, mais qui était déjà connue de Regiomontanus, qui la savait fausse et dont on attribuait déjà la provenance aux mathématiciens indiens. Il y affirme aussi détenir les secrets de la duplication du cube et de la trisection de l'angle.
approximation très mauvaise, dont il croit détenir la paternité, mais qui était déjà connue de Regiomontanus, qui la savait fausse et dont on attribuait déjà la provenance aux mathématiciens indiens. Il y affirme aussi détenir les secrets de la duplication du cube et de la trisection de l'angle. Joseph Juste Scaliger
Joseph Juste Scaliger
Alors qu'il négocie avec l'université de Leyde la succession de l'érudit Juste Lipse puis qu'il dirige celle-là, Scaliger ne veut pas reconnaître ses erreurs et s'enferre dans une stratégie désespérée. Précédé d'une réputation de savant et d'humaniste, il parvient à dissimuler ses erreurs pendant un temps aux yeux des gens ignorant la géométrie. Cazaubon l'applaudit, Dominique Baudier, ou Baudius, alors secrétaire du banquier Scipion Sardini le soutient[56], tandis que le mathématicien du roi Henri IV, Monantheuil se mure dans le silence et que Jacques-Auguste de Thou se détache peu à peu du 'prince des érudits'. Soutenu par une partie des protestants, qui voient en lui leur champion, Scaliger ira jusqu'à tenter de faire interdire (à Genève) l'impression des livres d'Adrien Romain contre sa cyclométrie[3].
Le 10 juin 1592, Scaliger écrit à Baudier :
« Au reçu de votre lettre voici ce que j'en écris ; j'entends les rumeurs répandues par Thrason (Viète). Il prétend que je cherche à éluder le débat c'est un mensonge. Donnez lui hardiment un démenti. Et à l'appui je lui enverrai par écrit de ma main mon défi avec promesse en cas de perte de lui payer une somme de 1000 à 1200 écus d'or. »Une dispute doit avoir lieu entre eux à Tours. Viète exige un débat public, un jury d'experts et un renoncement à faire appel de leur jugement[3]. D'avril à mai 1593, Scaliger écrit à Baudius pour tenter de régler les détails d'une telle rencontre. Dans cette correspondance Scaliger nomme Viète le moucheron et défend l'idée que la géométrie se juge d'elle-même. Mais le 21 mai, il est nommé à l'université de Leyde et dès lors, l'humaniste refuse de participer aux disputes publiques prévues à Tours et quitte la France en juillet sans donner suite à ses promesses. Ritter assure que Viète maintint ces rencontres, qu'il décrit comme des conférences publiques, où Viète annonce l'incommensurabilité de π (non démontrée). Conseillant aux mathématiciens de ne pas perdre leur temps à vouloir démontrer la quadrature, il cite :
« Nous ne comprenons pas comment la terre n'est qu'un point de l'immense espace du ciel ; quant à moi, je m'incline devant le mystère du très haut et je ne cherche pas un nœud sur un jonc (citation de Terence et de Plaute[3]). »Il termine avec sa formule donnant π comme un produit infini, où il croit déceler la preuve que le nombre d'Archimède ne peut être construit à la règle et au compas[3]. Partant de considérations géométriques[57] et au moyen de calculs trigonométriques qu'il maîtrise parfaitement, il sait en effet que :
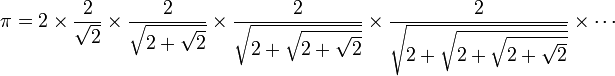
En date du 10 mai 1593, l'avocat Pierre Daniel d'Orléans[58], érudit en correspondance avec de nombreux savants et anciennement lié à Scaliger, écrit à Viète une lettre qui vante ces conférences et lui en réclame la publication.
« Je pense que vous serez d'accord avec moi qu'il est de l'intérêt de la science de pas laisser plus longtemps une aussi audacieuse espèce de gens tourmenter avec leurs écrits incendiaires les hommes de bien... »François Viète consigne cette lettre en tête de publication de son Varorium de rebus Mathemiticis, publié à Tours chez Mettayer l'année même et qui reprend - selon Ritter[6] - l'exposé de ses conférences (ce point de vue est néanmoins mis en cause par de plus récentes recherches[10] qui doutent que ces conférences aient eu lieu). Ritter mentionne également une citation à comparaître qui laisse présumer que Viète menaçait Scaliger - qu'il nomme ironiquement monsieur de l'Escale, professeur de grammaire - d'un procès pour diffamation[3]. Le 13 novembre 1593, François et son frère Nicolas hypothèquent par contrat tous leurs biens passés et à venir contre le prêt d'une somme de 2 000 écus. On ignore la destination de cette somme. Ritter la croit pour partie destinée à honorer le contrat avec Scaliger ou les frais de son second mariage. Viète s'est probablement mis en ménage avec sa seconde femme, Julienne Leclerc, dans ces années-là.
En 1594, devenu recteur de l'université de Leyde, Scaliger publie, quant à lui, une cyclotomie nouvelle, où il corrige quelques erreurs relevées par le chevalier Jean Errard de Bar-le-Duc et Ludolph van Ceulen de cette même université. En novembre, il en envoie quelques exemplaires à Pierre Pithou, érudit ami de Thou, qui en communique un à Viète[3].
L'année suivante, François Viète publie un Bouclier contre la cyclotomie nouvelle, tiré des impromptus géométriques de Monsieur Viète, œuvre ironique qui conduit Scaliger à déclarer le 4 mai, à Monantheuil :
« J'ai trouvé la quadrature mais je n'ai pas su si bien la démontrer qu'il n'y ait rien à reprendre. »Cependant, devant Cazaubon, le prince des érudits maintient que le périmètre du cercle est le six cinquième de l'hexagone inscrit. Scaliger publiera encore sur le sujet, de Leyde, un opuscule tout aussi infondé mathématiquement : Le Mesolabium. Viète lui répondra par un ironique Pseudo Mesolabium édité en 1595[59]. Adriaan van Roomen et Christophe Clau reprendront le flambeau en publiant respectivement in Archimédie circuli Dimensionae contra Josephum Scaligorum... et ces mots d'une dureté inouïe sous la plume de Clavius :
« Voici mon dernier mot : je ne puis aimer des hommes comme vous, payant comme on dit tribu à tous les vices ; je ne puis ne pas détester un homme aussi malhonnête aboyant après tous les gens de biens, après tous ceux de mérite, portant à bout les gens tranquilles. Ni les hommes ni Dieu, dont vous amassez sur votre terre la colère, ne peuvent plus supporter un homme comme vous, menteur, faux mathématicien, infâme, scélérat. »En comparaison de ces attaques, celles de Viète font preuve d'un grand respect pour l'érudit et l'homme de lettres protestant. Scaliger, après cela, ne dit plus un mot de cyclométrie. Il continuera néanmoins à distiller son venin contre Viète, rappelant en 1600 à Jacques-Auguste de Thou, qu'il lui avait appris à écrire son nom, et que son anagramme pouvait se lire
« Cur asinus faciet : 'Pourquoi l'âne le fera-t-il ? »Le problème d'Adrien Romain (Van Roomen)
Du 10 au 15 octobre 1594, Henri IV et son petit conseil sont réunis à Fontainebleau avec Monsieur de Villeroy et l'ambassadeur des États (de Hollande). Ce dernier, devant qui Henri IV fait étalage de la diversité du génie français, prétend qu'il n'y a pas de mathématicien en France, sous prétexte qu'il n'en figure aucun dans le défi qu’Adrien Romain a lancé aux mathématiciens du monde entier[10].
Liste des mathématiciens du défi de Roomen - Christopher Clavius
- Guido Waldo (marquis del Monte)
- Jean-Antoine Magin de Padoue [60]
- Grotius alias Jean-Christophe Cornets van Groot[61]
- Ludolph van Ceulen de Leyde
- Michel Coignet[62]
- Nicolas Peterson
- Simon Stevin de Bruges
- Tycho Brahé
- Valentin Otto (en)
- Bernard Lordel
- Jean Wander Wegede, ses élèves, Thomas Fien d'Anvers et Cornelius Opmer de Delft.
Cette célèbre polémique est narrée par Tallemant des Réaux en ces termes (historiette 46) :
Du temps d'Henri IV, un Hollandais, nommé Adrianus Romanus, savant aux mathématiques, mais non pas tant qu'il croyait, fit un livre où il mit une proposition qu'il donnait à résoudre à tous les mathématiciens de l'Europe ; or, en un endroit de son livre il nommait tous les mathématiciens de l'Europe, et n'en donnait pas un à la France. Il arriva peu de temps après qu'un ambassadeur des États vint trouver le Roi à Fontainebleau. Le Roi prit plaisir à lui en montrer toutes les curiosités, et lui disait les gens excellents qu'il y avait en chaque profession dans son royaume. « Mais, Sire, lui dit l'ambassadeur, vous n'avez point de mathématiciens, car Adrianus Romanus n'en nomme pas un de français dans le catalogue qu'il en fait. -- Si fait, si fait, dit le Roi, j'ai un excellent homme : qu'on m'aille quérir M. Viète. » M. Viète avait suivi le conseil, et était à Fontainebleau ; il vient. L'ambassadeur avait envoyé chercher le livre d'Adrianus Romanus. On montre la proposition à M. Viète, qui se met à une des fenêtres de la galerie où ils étaient alors, et avant que le roi en sortît, il écrivit deux solutions avec du crayon. Le soir il en envoya plusieurs à cet ambassadeur, et ajouta qu'il lui en donneroit tant qu'il lui plairait, car c'était une de ces propositions dont les solutions sont infinies.
Ut legi, ut solvi, note François Viète ultérieurement. « Aussitôt lu, aussitôt résolu ».
Le problème d’Adrien Romain que présente l’ambassadeur, et dont Viète donne une solution rapide, plus complète que celle de Ludolph van Ceulen consiste en la résolution d'une équation de degré 45 dans laquelle le géomètre et maître des requêtes reconnaît le partage d'un arc donné en 45 parts égales. Les exemples que donnent Romain à sa résolution l'indiquent clairement. La solution que donne Viète correspond à la corde d'un arc de 8 ° (soit
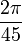 rd). Il lui est alors aisé de déterminer par la suite 22 autres solutions positives, les seules admissibles à l'époque et d'en présenter la liste le lendemain à l'ambassadeur.L'équation de Roomen
rd). Il lui est alors aisé de déterminer par la suite 22 autres solutions positives, les seules admissibles à l'époque et d'en présenter la liste le lendemain à l'ambassadeur.L'équation de RoomenÉcrit en langage actuel, le problème que soumet Adrien Romain revient à déterminer x tel que
- 45x − 3795x3 + 95634x5 − 1138500x7 + 7811375x9 − 34512075x11 + 105306075x13
- − 232676280x15 + 384942375x17 − 488494125x19 + 483841800x21 − 378658800x23
- + 236030652x25 − 117679100x27 + 46955700.x29 − 14945040x31 + 3764565x33
- − 740259x35 + 111150x37 − 12300x39 + 945x41 − 45x43 + x45 = N
où N est donné. Cette équation est exposée dans : Idée mathématique partie un, imprimée à Louvain en 1593.
Van Roomen ajoute que pour
la solution est
et donne quelques autres issues de division en 45 morceaux d'un arc complémentaire au côté d'un polygone inscrit dans le cercle. Pour plus de détail, on consultera, la notice que Frédéric Ritter à consacré à Viète dans la revue occidentale philosophique, sociale et politique (2d série, volume X), page 29 [6]
Quand, en 1595, Viète publie sa réponse à Adrien Romain, sous le titre Ad problema quod omnibus mathematicis totius orbis construendum proposuit Adrianus Romanus, Francisci Vietae responsum. Paris, Mettayer, 1595, in 4 , 16 fol, il propose en retour au mathématicien belge une autre énigme : la résolution à la règle et au compas du problème des contacts ou problème d’Apollonius de Perga dont la solution s'est perdue depuis l'antiquité et que Regiomontanus a pu résoudre par l'algèbre, mais sans donner de construction géométrique. C'est le dernier problème d'un traité perdu d'Apollonius, à savoir trouver un cercle tangent à trois cercles donnés. Dans ses mémoires, Adrien Romain affirme l'avoir résolu en aussi peu de temps que Viète a résolu le sien, c'est-à-dire dès réception. Toutefois, sa solution passe par la construction de l'intersection de deux hyperboles, ce qui ne respecte pas les contraintes de construction à la règle et au compas imposées par Euclide.
« un homme éminent, un véritable mathématicien qui ne se laisse pas chatouiller par cet aiguillon de la gloire qui fait perdre la tête à tant d'autres : c'est un Français, nommé François Viète, conseiller du Roi et maître des requêtes au Parlement. Ne pouvant souffrir, comme il dit lui-même, qu'un Belge ou un Romain lui ravit sa gloire, il répondit surabondamment à mon défi par un traité d'une remarquable érudition, »dit Van Roomen de Viète[63].
François Viète publie sa propre solution en 1600, dans l'Apollonius Gallus.
« Éminent Adrien, lui écrit-il, tant qu'on touche le cercle par des hyperboles, on ne le touche pas finement. »A quoi, le professeur de Wurzbourg demande à des juges italiens de trancher (on ignore leur jugement). Selon ses propres mots :
« Nous sommes tous des hommes... c'est pourquoi j'ai voulu choisir un juge ... et qui ne penchât pour aucune des parties en cause. La lutte étant ouverte entre un Français et un Belge, j'ai récusé tous les juges pris dans ces deux nations, et c'est vous, qui résidez dans cette ville où siège le juge suprême de l'univers (Rome), c'est vous que j'ai voulu prendre pour arbitre : je vous offre donc ma réponse : examinez-la, et s'il vous convient de vous adjoindre des juges comme Christophe Clavius de la Société de Jésus, Jean Antoine Magin, l'illustre marquis de Monte, ou tels autres que vous voudrez, usez-en à votre discrétion : j'attendrai votre sentence et je m'y soumettrai en toute humilité.[63] »De Thou raconte dans son histoire universelle qu'Adrien Roman abandonne son université de Wurtzbourg dès réception de cette solution (vers 1597) son université de Wurtzbourg, selle son cheval et se rend à Paris puis à Fontenay-le-Comte, où Viète réside alors. On ne trouve nulle part trace de cette légende dans les lettres d'Adrien Romain. Aux dires de De Thou, le mathématicien belge demeure un mois avec Viète et s'initie aux méthodes de l'algèbre nouvelle. Les deux hommes deviennent amis, Viète raccompagne Romain à la frontière et le défraie de ses dépenses. On peut douter de cette nouvelle historiette, elle illustre néanmoins en quelle estime on tenait les exploits du maître des requêtes à la cour de France.
La résolution du problème de Romain (ou Roomen) et la restauration du traité perdu d'Apollonius ont en effet un retentissement presque immédiat en Europe. Elles valent à Viète l'admiration de nombreux mathématiciens à travers les siècles. Pour le problème des contacts, il ne traite pas toutefois des cas particuliers (cercles confondus, tangents entre eux, etc.), reconnaît que le nombre de solutions dépend de la position relative des trois cercles et expose les dix situations résultantes. Descartes complètera en 1643 le théorème des trois cercles d'Apollonius, aboutissant à une équation quadratique de 87 termes dont chacun est un produit de six facteurs (ce qui rend la construction effective humainement impossible par ce biais)[64],[65]. Pierre de Fermat l'étendra aux Sphères puis Frederick Soddy(1936), dans un des cas particuliers[66],[67].
Notaires, Tabellions et Gardenotes
Viète, qui est épuisé par son travail de maître de requêtes et déchiffreur, obtient alors du roi quelques vacances. L'occasion s'en présente lorsque éclate la rébellion des Notaires : les Suisses mercenaires qui se battent au côté des armées d'Henri IV réclament depuis des années le paiement de leurs gages. Ils menacent de changer d'alliance et pour satisfaire leurs exigences, le roi et son conseil décident d'un nouvel impôt. Celui-ci prend pour cible les notaires, auquel un édit de mai 1597 ordonne de remettre leur charge contre remboursement afin d'en répartir aux enchères les nouveaux privilèges, devenus héréditaires et unifiés[68]. Les notaires refusent ce qu'il considèrent comme une spoliation et refusent de produire les actes d'achat de leurs charges. Les autres officiers royaux se solidarisent avec eux et les commissaires nommés par Henri IV sous la direction de Monsieur Audouyn de Montherbu[69] se voient dans l'incapacité de faire appliquer l'édit royal. Une nouvelle mouture, décidée en novembre 1597[6] et qui se limite à taxer les charges pour leur conférer un caractère unique et héréditaire ne connaît pas plus de succès. Il faudra que le roi et son conseil donnent licence aux commissaires de taxer ces charges selon leur convenance pour qu'enfin cet impôt, qui trouvera son aboutissement dans la Paulette, voit le jour et permette à l'État d'honorer ses dettes envers les Suisses.
François Viète est le commissaire nommé par Henri IV pour faire rentrer dans l'ordre les notaires du Poitou, de la Rochelle et de Lusignan. Il s'en acquitte de 1597 à 1599, profitant de ce congé pour rétablir sa santé déjà chancelante. Accompagnée d'un huissier et d'un clerc de notaire parisien[10], il loge alors à Fontenay-le Comte, où il a la douleur de perdre ses sœurs Jeanne (1595) et Julienne (1597) et de partager leurs biens avec ses deux frères et leurs héritiers. Dans la même période (1596), il cède une maison et le fermage de ses terres de Fontenay à son frère Nicolas en remboursement de ce qu'il doit, contre une rente de 40 écus l'an[3].
Ces actes nous donnent l'occasion de connaître sa signature.
Dernières publications mathématiques
En 1600, le mathématicien ragusien Ghetaldi le rencontre à Paris et Viète lui communique quelques uns de ses ouvrages, dont son Harmonicon Celeste. Ghetaldi publie chez D. Leclerc l'Apollonius Gallus et le De Numerosa Potestum[70]. Une lettre de la main du ragusien, daté du 15 février, et destiné à son maître, Michel Coignet donne de Viète l'image d'un homme complaisant et généreux :
« Votre seigneurie sait le désir que j'avais de connaître M. Viète, depuis que j'ai vu quelques-uns de ses ouvrages. Cela a été cause que, me trouvant à Paris pour d'autres affaires personnelles, j'ai voulu, avant de partir pour l'Italie, lui faire visite. Sa connaissance m'a prouvé qu'il était non moins affable que savant. Non seulement il m'a montré beaucoup de ses ouvrages encore inédits, mais il me les a confiés, afin que je les visse dans ma maison et à ma commodité... comme je le priais instamment de le publier, il commença à s'excuser, disant qu'il ne le pouvait faire, et n'avait pas la commodité de pouvoir le revoir et le polir. Et véritablement il est plus empêché la grande partie du temps dans les affaires de S. M. très-chrétienne, étant du conseil d'État et maître des Requêtes." »La lettre qui ouvre l'Apolonius Gallus et tutoie Viète semble également dans son esprit.
« J'ai beaucoup de raisons de t'admirer, illustre ami, car tu vis la plupart du temps dans le monde des lois et des affaires publiques et cependant tu es habile et doué pour tout ce qui touche aux sciences, et surtout par cette connaissance du jugement qui d'autre part t'as permis de t'élever dans la connaissance et l'étude des mathématiques... Je considère comme un honneur d'obtenir de toi qui es perpétuellement en relation avec les affaires politiques et les affaires publiques de par les ordres du roi, que communiques avec ceux qui désirent s'instruire.[7]. »La même année, ses secrétaires Pierre Aleaume et Charles Du Lys acceptent la mission de traduire en français les œuvres de leur maître. Henri IV confère à Jamet Mettayer un privilège exceptionnel pour la publication de cette œuvre, que l'imprimeur dit avoir payée, mais qui ne verra, hélas, jamais le jour[7].
L'affaire du calendrier
En 1582, le pape Grégoire XIII avait demandé par la bulle Inter Gravissimas aux rois catholiques de passer du calendrier julien au calendrier actuel. Cette réforme avait été préparée avec soin, mais il y manquait une explication. Les calculs du médecin calabrais Aloysius Lillius ou Giglio, avaient été repris après son décès par le conseiller scientifique des papes, Christopher Clavius. Dès le début de ces travaux, Scaliger et Michael Maestlin, deux protestants, avaient attaqué le calendrier nouveau style mais leurs critiques avaient été aisément rejetées par le mathématicien romain[10].
À partir de 1593 (Huitième Livre des réponses sur diverses questions mathématiques) et jusqu'à sa mort, Viète prend la plume à son tour et critique sévèrement l'interprétation de Clavius. En 1600, il forme un calendrier parallèle à celui de l'église romaine[71], qu’il fait imprimer et qu'il communique au neveu du Pape Clément VIII, le cardinal Aldobrandini, lors de son passage à Lyon, comme négociateur entre Henri IV et le duc de Savoie[6]. Parallèlement, il saisit la congrégation chargée de réformer le calendrier. Clavius, qui préside cette congrégation écarte sans y prêter attention ses critiques et ce nouveau calendrier mais Théodose de Perpino, un des élèves du jésuite de Bamberg s'insurge au nom de la compagnie de Jésus que Viète ait fait circuler un calendrier perpétuel imitant le calendrier officiel[3].
Se voyant méprisé par son adversaire, Viète accuse alors Clavius, dans une série de pamphlets dont l’Adversus C. Clavium expostulatio (fin 1602), d'introduire des corrections et des jours intercalaires de façon arbitraire, et de s’être mépris sur la signification des travaux de son devancier, notamment dans le calcul du cycle lunaire. Viète est particulièrement étonné que, certaines années, la date de Pâques du nouveau calendrier ne respecte pas les consignes données par les pères de l'église lors du Concile de Nicée.
Dans cet ouvrage, le dernier qu'il publie, il se montre d'une rare violence contre son adversaire :
« Personne ne peut être juge ni juger sa propre cause, affirme-t-il dans son réquisitoire de 1602, Ce n'est pas ainsi qu'on procède en justice... J'ai démontré que vous êtes un faux mathématicien et un faux théologien... toutes vos fanfaronnades sont sans aucune valeur... Vous vous moquez du Souverain Pontife, allant comme un âne devant la paille.. »Viète eut sans doute tort de s'attaquer à ce privilège des papes. A-t-il cru qu'il pouvait devenir le « roi du temps » comme l'affirme Dhombre[72] ? Ce calendrier, étudié par l'érudit autrichien Ferdinand Kaltenbrunner[73], est une composition mathématique[74] qui ne semble avoir en réalité d'autres but que de démasquer Clavius. Il est vrai que Viète tenait Clavius en piètre estime ainsi que l'atteste de Thou[24] :
« Il disait, que Clavius était très-propre à expliquer les principes des mathématiques, & à faire entendre avec beaucoup de clarté, ce que les auteurs avaient inventé, et écrit en différents traités avec beaucoup d'obscurité : qu'à l'égard de sa science il écrivait de manière à faire croire qu'il ne venait que d'apprendre ce qu'il mettait sur le papier: Qu'on n'y trouvait rien de lui : qu'il se contentoit de copier les auteurs, qui avaient écrit avant lui, et d'ordinaire sans les citer, en sorte que ses ouvrages n'avaient d'autre utilité que de rassembler dans un meilleur ordre ce qui se trouvait dispersé & confondu dans d'autres écrits : que cependant il fallait avouer qu'il rendait si clair et si intelligible ce qu'il y avait d'obscur dans ces ouvrages, qu'on pouvoir dire qu'il se les rendait propres. »Focalisé sur l'idée toute pythagoricienne que 19 ans solaires correspondait à 20 années lunaires (peu s'en faut), et persuadé que le très haut l'avait voulu ainsi, Viète produit alors un calendrier pseudo-Grégorien d'une régularité (sur 3400 ans) que n'a pas celui du mathématicien des papes. Les Coperniciens, qu'il cite dans ses récriminations contre le jésuite de Bamberg savent pourtant dès cette époque qu'une telle période voisine plutôt les 3424 ans... En mars 1603, Clavius lui répond enfin dans son Explicatio. Il le fait avec beaucoup de respect, rendant hommage à l'intelligence de Viète. Il le prie néanmoins de ne plus l'importuner. Dans son bief paru le même jour, et justifiant les calculs de la commission chargée de peaufiner la réforme, Clément VIII se montre bien plus sévère[10] et dénonce la prétention d'un certain François Viète de produire un calendrier perpétuel plus parfait que celui de l'église apostolique et romaine. Ignorent-ils que Viète est mort deux semaines plus tôt, à Paris ?
Une fin précoce
Dans les dernières années de sa vie, Viète fut attaqué dans un pamphlet par son ancien amanuensis Tarporley, devenu l'élève d'Harriot[75] sous le nom de plume de Poltrey ou Poulterey[76]. Toute trace de ce pamphlet semble avoir disparu depuis la mention qu'en a fait Anthony H. Wood.[77]. Selon certains témoignage, l'apparition de Tarporley dans la vie de François Viète daterait seulement de ces dernières années. Le recteur de Syon se serait-il déguisé sous le nom de Poltrey pour lui servir de scribe[78] ? Cela paraît peu vraisemblable.
Malade, et épuisé par le travail, Viète s'est dégagé du service du roi et le 14 décembre 1602 une lettre d'Henri IV au chancelier de Pomponne de Bellièvre ordonne qu'on lui verse le solde de son compte. La résiliation de ses charges lui permet de toucher 20 000 écus, mille écus d'or[79]qu’on trouve à son chevet, après sa mort[80].
Hughes de Salins, médecin, né à Beaune en 1632 et mort en 1710, affirme à ce propos[81] :
« Il ne mourut pas subitement mais d'une de ces affections impitoyables résultant de ceux-ci des travaux qui le minait depuis plusieurs années... Quelques jours avant sa mort, il sentit sa fin prochaine ; il avait écrit - d'une main ferme et assurée - à Monsieur de Rosny sur le déchiffrement des écritures secrètes... »Un dernier mémoire sur des questions de cryptographie, qui rend caduques toutes les méthodes de chiffrement de l'époque[82].
Hughes de Salins, ajoute[83]:
« Estant fort malade, le président Dolet le pria de se confesser à un prestre, et luy remonstra que s'il mouroit sans cela, sa fille ne trouveroit pas de party, comme fille d'un » athée. Ce qui le fit resoudre à se confesser. Pour le medecin, il dit qu'il n'en vouloit point, si ce n'estoit Duret, à la charge qu'en ses visites, il l'entretiendroit de mathematiques, esquelles on disait qu'il estoit sçavant.[10] »Cette version des derniers instants de François Viète a parfois été jugé suspecte. Louis Duret, le médecin des rois Charles IX et Henri III, étant disparu avant 1595 et son fils, l'avocat Claude Duret n'ayant aucune qualité de médecin (quoique s'étant beaucoup occupé d'astrologie). Il peut aussi s'agir de son autre fils Jean, médecin d'Henri IV, dont l'héritier, Noël sera lui-même cosmographe du Roi, au XVIIe siècle et publiera une partie des œuvres posthumes de Viète. Les manuscrits d'Hughes de Salins, qui se trouvaient dans la bibliothèque de M. Feuillet de Conches ayant disparu depuis leur vente en mai 1887[7], on demeure prudent sur ces propos.
Viète meurt le 23 février 1603[24], laissant au monde deux filles, Suzanne, à peine nubile, née de Julienne Le Clerc (ou Leclere) avec laquelle on ne sait si Viète était marié (Fillon affirme que cette dernière est fille d'un conseiller du parlement de Paris[84]) ; et Jeanne, son aînée, née de Barbe Cottereau[85] et déjà mariée. La première meurt en janvier 1618, à Paris. La seconde, a épousé le conseiller du Parlement de Bretagne Jean Gabriau et meurt, quant à elle, en 1628[86].
Le mathématicien écossais, Alexander Anderson, que Pierre et Jacques Aleaume chargent d'éditer le reliquat des manuscrits de Viète, affirme que la mort de son maître fut une grande perte et il écrit à ce propos :
Les portraits qu'on a de lui sont des créations du XVIIe siècle, dues à Daniel Rabel, peut-être d'après des dessins de son père Jean Rabel[3], peintre officiel à la cour de France et décédé quelques jours après le mathématicien.
L'œuvre de Viète
Une œuvre multiple
Outre ses travaux de maître des requêtes, Viète consacra ses loisirs aux mathématiques, il en sortit des livres, qu'il faisait imprimer à ses frais et qu'il offrait à ceux de ses amis qui pouvaient les comprendre ou aux mathématiciens européens de son temps qui entraient en correspondance avec lui. Comme son travail l'amena à déchiffrer les codes secrets des ennemis du roi de France et de Navarre et qu'il suivit de près les avancées de l'astronomie, son œuvre prit quatre directions, dans lesquelles son cerveau fécond apporta à chaque fois des changements considérables.
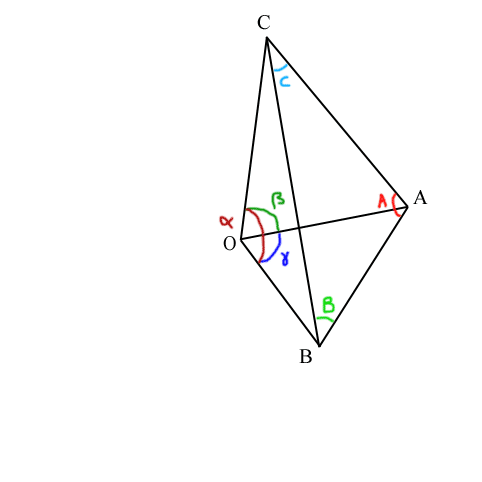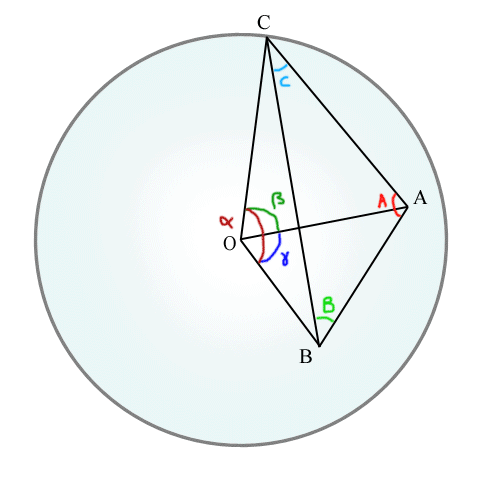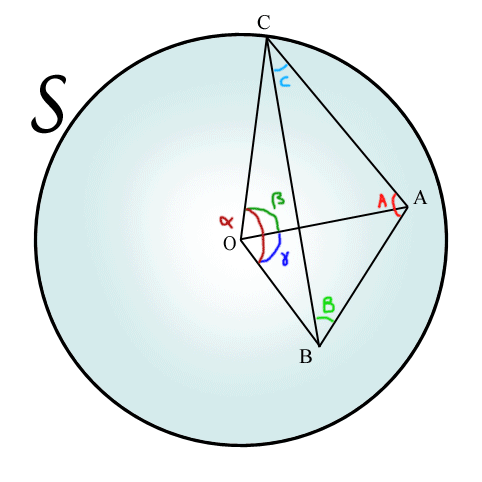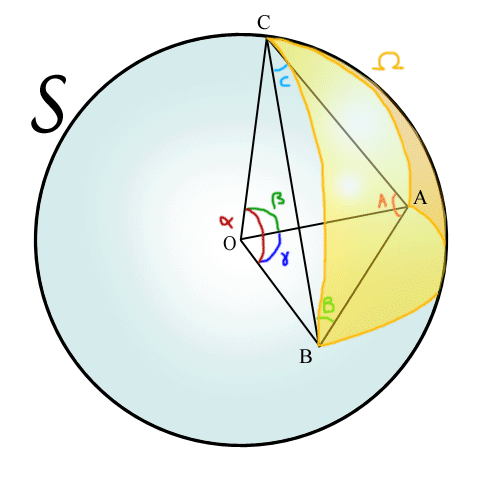 traingle sphérique
traingle sphérique
- En géométrie, Viète fournit les "formules" des lignes trigonométriques, dont il donne des tables plus précises que celles de Regiomontanus et de Georg Joachim Rheticus et développe la trigonométrie sphérique, en quoi il se montre l'héritier d'Albategni. Au passage il découvre les relations de polarité des triangles sphériques[88] et semble avoir pressenti le rôle de l'inversion dans les démonstrations de géométrie plane.
Il donne notamment les formules reliant les angles et les longueurs des triagles rectangles découpés sur la sphère ; ce qu'on écrit en langage moderne[89]:
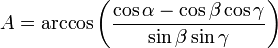 dont on trouvera les démonstrations dans Gergonne[90]
dont on trouvera les démonstrations dans Gergonne[90]- En algèbre, dont le terme lui semble corrompu et qu'il renomme analyse spécieuse, il élabore une première forme de calcul littéral destinée à traduire les problèmes géométriques sous une forme générale, ce qui fait de lui le fondateur de notre algèbre moderne et ce pourquoi il est connu aujourd'hui (voir paragraphe ci-dessous).
- En cryptographie, où il a excellé, il laisse un court manuscrit indiquant des méthodes de déchiffrement[91] qui forment, historiquement, la première marche de cette discipline[92].
- Pour l'astronomie, vers laquelle concourent tous ces travaux, il laisse un manuscrit (non publié à ce jour) qui donne aux astronomes des méthodes géométriques afin de mieux traduire le mouvement des planètes, tant du point de vue de Ptolémée que de Copernic, étant lui-même devenu adepte d'un système intermédiaire, semblable à celui de Tycho Brahé. Enfin, dans cet Harmonicon Celeste, on trouve plus d'une décennie avant Kepler, la découverte de la trajectoire elliptique des planètes.
Au cœur de cette invention, se trouve l'héritage grec, que Viète tente de restaurer, les avancées du monde arabo-musulman et celles des calculateurs européens. En proposant, dans son Isagoge, de travailler avec des symboles, Il se veut le rénovateur d'une mathématique qu'il croît oubliée ; en donnant les premières formes de calculs formels, son apport personnel fait de lui - et malgré lui - un fondateur. Pour autant, il demeure beaucoup de chemin à faire après Viète pour que l'écriture algébrique trouve enfin sa stabilité et ses travaux sont empreints d'archaïsmes. Ce sera l'œuvre de ses héritiers, directs et indirects, Thomas Harriot, Alexander Anderson, James Hume, Pierre de Fermat et René Descartes. Écrits en latin, car à l'usage des autres savants européens, abondants de néologismes et de citations grecques, incomplets dans leur formalisme, ces ouvrages sont rares, peu accessibles et, aujourd'hui, forts chers. Son nom a été au pinacle, puis lentement oublié, gommé par la gloire du philosophe de la Haye auprès des encyclopédistes, puis retrouvé et restauré au XIXe siècle par de courageux érudits.
Détail des éditions anthumes
- Entre 1564 et 1568, Viète rédige pour son élève, Catherine de Parthenay, quelques manuels d'astronomie et de trigonométrie et un traité de cosmographie, qui préfigure le livre jamais publié : Harmonicon Cœleste auquel il apportera des corrections toute sa vie[93].
- À partir de 1571, il fait publier à ses frais et avec de grandes difficultés d'impression : Universalium inspectionum ad canonem mathematicum liber singularis. Paris, Mettayer, 1579, 164 fol ; un ouvrage de trigonométrie, abrégé en Canon mathématique, où il présente de nombreuses formules sur les sinus et les cosinus. Il y fait un usage inhabituel pour l'époque des nombres décimaux. Ces tables trigonométriques complètent celles de Regiomontanus (De triangulis omnimodis, 1533) et de Rheticus (1543, annexées au De revolutionibus... de Copernic). Viète, mécontent des fautes d'impression qu'il renfermait, chercha à en retirer de la circulation tous les exemplaires[94].
- En 1589 : Deschiffrement d'une lettre escripte par le Commandeur Moreo au Roy d'Espaigne son maître. Tours, Mettayer, 1590, 20 p.
- Deux versions de l'isagoge :
- Ce traité In artem analyticem Isagoge (Introduction à l'art de l'analyse), est considéré comme un texte fondateur de l'analyse (par contraste avec la synthèse) pour les Modernes[95]. C'est dans la seconde édition qu'apparaissent les règles de calcul algébrique.
- En 1591 encore, Zeteticorum libri quinque. Tours, Mettayer, 24 folio, qui forment les cinq livres des Zététiques. Il s'agit d'un recueil de problèmes, issus de Diophante, et résolus en utilisant l'art analytique.
- Entre 1591 et 1593, Effectionum geometricarum canonica recensio. Sd, 7 fol., qui fait le lien entre des expressions et équations algébriques du second degré et certains problèmes géométriques.
- En 1593,
- Un complément sur les problèmes géométriques : Supplementum geometriae.Tours, 21 fol. ;
- Variorum de rebus mathematicis responsorum liber VIII (Huitième Livre des réponses variées). Tours, Mettayer, 1593, 49 fol, à propos des défis de Scaliger, dans lequel il revient sur les problèmes de la trisection de l'angle (dont il reconnaît qu'il est lié à une équation du troisième degré), de la quadrature du cercle, de la construction de l'heptagone régulier, etc. L'année suivante, il donnera contre le même Scaliger : Munimen adversus nova cyclometrica. Paris, Mettayer, in 4, 8 fol.
- En 1595 Ad problema quod omnibus mathematicis totius orbis construendum proposuit Adrianus Romanus, Francisci Vietae responsum. Paris, Mettayer, in 4 , 16 fol ; texte où se trouve la solution du problème d'Adrien Romain.
- En 1600, De numerosa potestatum ad exegesim resolutione. Paris, Le Clerc, 36 fol ; œuvre qui fournit des moyens d'extraction de racines et de solutions d'équations de degré au plus 6.
- En 1600, Apollonius Gallus. Paris, Le Clerc, in 4, 13 fol ; qui traite des problèmes de points de contacts de trois cercles et où il se désigne lui-même comme l'Apollonius français.
- Entre 1600 et 1602, il rédige, à propos du calendrier de Clavius,
- Fontenaeensis libellorum supplicum in Regia magistri relatio Kalendarii vere Gregoriani ad ecclesiasticos doctores exhibita Pontifici Maximi Clementi VIII. Anno Christi I600 jubilaeo. Paris, Mettayer, in 4, 40 fol ;
- et aussi Francisci Vietae adversus Christophorum Clavium expostulatio. Paris, Mettayer, in 4, 8 p qui exposent ses thèses contre Clavius.
- un manuscrit perdu, devait traiter de Mécanique. Gailée en a eu connaissance[96] on connaît aussi une feuille de correspondances ésotériques, rédigées par Viète et qui associe l'air aux éléments, le sang aux humeurs, le poumon et la tête au corps, les maux de têtes et les inflammation du foi au maladies, l'aigle, la caille et le poulet, aux oiseaux ; le chêne et le sureau aux arbres, le réglisse et la mirabelle aux herbes, l'émeraude et le saphir aux pierres et l'étain aux métaux ; elle ressemble davantage à un questionnaire de Proust qu'à une recette alchimique. Cette table analogique des corps supérieurs et inférieurs, est copiée - d'après Viète - de la main de Vaulezard[7]
L'Algèbre nouvelle
Les mathématiques de la Renaissance se plaçaient sous la double égide des mathématiques grecques, dont les outils l'empruntent à la géométrie et des mathématiques arabes, qui fournissent des procédures de résolution dégagées de toute intervention géométrique[97]. À l'époque de Viète, l'algèbre oscille donc entre l'arithmétique[98], qui donne l'apparence d'un catalogue de règles et la géométrie qui manifeste toute la rigueur axiomatique que lui a donné Euclide. Parallèlement, les Italiens ont développé avec Luca Pacioli, Scipione del Ferro, Niccolo Fontana Tartaglia, Ludovico Ferrari, et surtout Raphaël Bombelli (1560) une technique de résolution des équations du troisième degré qui annonce un âge nouveau. D'un autre côté, l'école allemande de la Coss, le mathématicien anglais Robert Recorde (1550) puis le Hollandais Simon Stevin (1581) ont introduit un début de notation algébrique, l'usage des décimaux et des exposants. Pour autant, les solutions négatives sont considérés le plus souvent comme absurdes et les nombres complexes demeurent tout au plus une vue de l'esprit ; près d'un siècle après leur invention Descartes, les décrira encore comme des nombres imaginaires. Seules les solutions positives sont considérées, et l'idée de justifier géométriquement les raisonnements algébriques est courante[99]. Enfin, les mathématiciens français ont accompli un travail novateur considérable, et parfois ignoré : Pierre de la Ramée, dit Ramus, a redonné leur place aux mathématiques dans l'université. Humaniste, possédant aussi bien le grec que le latin et l'hébreu, il a refondé la logique, rénové l'alphabet; ses « élèves », Guillaume Gosselin et Jacques Pelletier du Mans ont introduit la notation formelle des systèmes numériques de deux équations à deux inconnues (sans paramètre).
La tâche qui attend les mathématiciens est double : s'il veulent faire progresser leur science, il leur est nécessaire de géométriser l'algèbre, afin de lui donner un fondement rigoureux et d'algébriser la géométrie, afin de permettre le calcul analytique dans le plan. Cette double tâche, sera accomplie successivement par Viète, Harriot, Descartes et Fermat [100]. Ouvrant la voie de la formalisation, Viète est conscient de la nécessité de donner à l'algèbre un fondement aussi impeccable que celui de la géométrie et c'est à cette fin qu'il remplace l'algèbre numéreuse des procédures (celle de l'al jabr et de la muqabala) par une analyse symbolique, logistique spécieuse ou Algèbre nouvelle, nom que lui donnera le traducteur Antoine Vasset (alias Claude Hardy). Ce faisant, il n'hésite pas à affirmer que, grâce à cette nouvelle algèbre, tous les problèmes pourront être résolus (Nullum non problema solvere).
Cette rupture, Viète en a particulièrement conscience. Dans sa dédicace de l'Isagoge à Catherine de Parthenay il affirme en effet :
- « Toute chose nouvelle se présente ordinairement à son origine rude et informe, pour être polie et perfectionnée dans les siècles suivants. L'art que je produis aujourd'hui est un art nouveau, ou du moins tellement dégradé par le temps, tellement sali et souillé par les barbares, que j'ai cru nécessaire de lui donner une forme entièrement neuve, et après l'avoir débarrassé de toutes ses propositions erronées, afin qu'elle ne retînt aucune souillure, et qu'elle ne sentît la vétusté, imaginer et produire des mots nouveaux auxquels les oreilles étant jusqu'à présent peu habituées, il sera difficile que plusieurs personnes n'en soient pas dès le seuil même épouvantées et offensées[101]. »
Dans les conditions de l'époque, il manque néanmoins à Viète le symbole de la multiplication « × » (qui sera donné par William Oughtred vers 1631), le symbole d'égalité « = », déjà présent chez Robert Recorde, ainsi que les symboles de comparaison « < » et « > », qui seront rajoutés par les éditeurs de Thomas Harriot et peut-être Nathanael Tarporley. Il lui manque aussi du temps et des élèves, capables d'illustrer brillamment sa méthode. Viète met des années pour publier, tant il est méticuleux, de plus, il publie peu comme le souligna Champfort[102] :
- « Les poêtes... feraient à l’égard de leurs ouvrages ce que le fameux mathématicien Viète faisait à l’égard des siens, dans un tems où l’étude des mathématiques était moins répandue qu’aujourd’hui. Il n’en tirait qu’un petit nombre d’exemplaires qu’il faisait distribuer à ceux qui pouvaient l’entendre et jouir de son livre, ou s’en aider. »
Surtout, il effectue un choix très particulier pour séparer les variables des inconnues. Probablement influencé par les notations de Pierre de La Ramée mais aussi par l'hébreu (que connaît son élève, Catherine de Parthenay[103]), il sépare l'alphabet en consonnes (pour les paramètres) et voyelles (réservées aux inconnues). Ce choix s'avèrera désastreux pour la lisibilité et Descartes, en lui préférant les premières lettres pour désigner les paramètres et les dernières pour les inconnues, montrera moins de respect des traditions grecques et hébraïques, mais une plus grande perspicacité dans la compréhension humaine.
Exemple d'écriture de Viète 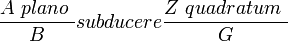
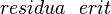
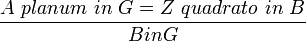
Viète demeure également prisonnier de son époque sous plusieurs aspects. En premier lieu, fidèle à la géométrie grecque, et héritier spirituel de Pierre de La Ramée, il ne traite pas les longueurs comme des nombres. Son écriture garde la trace de l'homogénéité ; ce qui ne simplifie pas sa lecture. Il ne reconnaît pas les complexes de Bombelli, et manifeste le besoin - vécu comme une nécessité - de doubler ses réponses algébriques par une construction géométrique. Bien qu'il ait probablement conscience que l'algèbre nouvelle suffise à donner la solution d'un problème, il suit en cela l'esprit du temps et ces archaïsmes entacheront bientôt sa réputation.
Toutefois, de nombreuses nouveautés apparaissent chez lui : les formules du binôme, qui seront reprises par Pascal et Newton ; les relations entre coefficients et racines d'un polynôme, qu'en anglais, on nomme la formule de Viète[104], l'apparition du premier produit infini, la reconnaissance du lien entre trisection de l'angle et équation du troisième degré...
Car enfin, Viète est le premier mathématicien à introduire des notations pour les données du problème (et pas seulement pour les inconnues). Idée neuve, qui peut en partie s'expliquer par ses études juridiques ; species désignant dans le jargon des avocats l'ensemble de leurs clients[105]. De ce fait, en accord avec Serfati, on considère généralement sa représentation symbolique de l'indéterminée comme une innovation majeure de la fin de XVIe siècle[106]. Son algèbre ne se limite plus à l'énoncé de règles mais s'appuie sur une axiomatique et sur un calcul formel efficace, où les opérations agissent sur les lettres et où les résultats peuvent s'obtenir à la fin des calculs par un simple remplacement. Cette démarche, qui est au cœur du procédé algébrique contemporain est une étape fondamentale dans le développement des mathématiques. En cela, Viète transforme définitivement l'algèbre concrète en une logistique symbolique, instrument d'une nouvelle géométrie[107] et marque réellement l'instant où s'accélère la rupture avec l'algèbre médiévale (d'Al-Khawarizmi à Stevin) et où s'ouvre la période moderne[108].
Parmi les problèmes que Viète aborde avec cette méthode, on trouve la résolution complète des équations du second degré de la forme
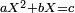 et des équations du troisième degré de la forme
et des équations du troisième degré de la forme 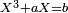 avec a et b positifs (Viète pose les changements de variable successifs :
avec a et b positifs (Viète pose les changements de variable successifs : 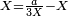 puis
puis 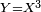 et se ramène ainsi à une équation du second degré).
et se ramène ainsi à une équation du second degré).Écrite essentiellement en latin, son œuvre pénétra toute l'Europe. Après la publication de l'Isagoge, et surtout après les publications d'Alexander Anderson, de Ghetaldi et de Jean de Beaugrand, les mathématiques ne s'écriront plus de la même manière. De 1591 à 1649, date de la réimpression des œuvres du philosophe René Descartes, les mathématiciens européens adoptent sa façon générale de voir. Les astronomes, les opticiens, vont écrire dans son langage sous l'influence de ses élèves, et les traductions de Vasset, de Jean-Louis Vaulezard de James Hume vont encore l'enrichir, de sorte qu'après 1630, de nombreux mathématiciens, dont Fermat, Schooten Huyghens, et Newton, écriront d'abord à la manière de Viète, avant de se débarrasser de ses contraintes d'homogénéité.
L'art de bien raisonner
À partir de 1591, Viète, qui dispose d'une certaine fortune personnelle, ce qui le distingue parmi les mathématiciens, commence à publier à ses frais, et à l'usage de ses amis, l'exposé systématique de sa théorie mathématique, qu'il nomme « logistique spécieuse » (de specis : symbole) ou art du calcul sur des symboles. Il développe d'abord les fondements de cette nouvelle algèbre dans son Isagoge, puis en donne la même années des applications essentielles dans ses Zététiques. D'autres livres viendront compléter l'exposé de cette théorie, qui permet de résoudre des familles d'équations algébriques de degré 2 à 4 en donnant un sens géométrique à ces résolutions.
La logistique spécieuse s'accompagne de surcroît d'un art de bien raisonner, qui procède en trois temps :
- Dans un premier temps, on note toutes les grandeurs en présence, ainsi que leurs relations, en utilisant un symbolisme approprié développé par Viète. On résume ensuite le problème sous forme d'une équation. Viète nomme cette étape la zététique. Il note les grandeurs connues par des consonnes (B, D, etc.) et les grandeurs inconnues par des voyelles (A, E, etc.).
- L'analyse poristique permet ensuite de transformer et de discuter l'équation. Il s'agit de trouver une relation caractéristique du problème, la porisma à partir de laquelle on peut passer à l'étape suivante.
- Dans la dernière étape, l'exégétique, on revient au problème initial dont on expose une solution par une construction géométrique ou numérique, s'appuyant sur la porisma.
On donne ci dessous le contenu d'un de ces livres de Zététiques, d'autres sont traduits à cette adresse:
Le Troisième livre des ZététiquesViète résout, algébriquement, puis géométriquement, en mêlant le formalisme et la rhétorique les 16 problèmes suivants qu'on traduit en langage moderne :
Sachant x,y,t, en progression géométrique (c'est-à-dire que
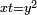 ); déterminez-les, pour a et b donnés, si :
); déterminez-les, pour a et b donnés, si :- y = a et x − t = b
- y = a et x + t = b
Dans un triangle rectangle, de base x et de hauteur y, d'hypoténuse h, déterminez-les, pour a et b donnés, si :
- y = a et h − x = b
Il fait remarquer au passage que x + h,y,x + h sont alors en progression géométrique et l'utilise pour résoudre :
- y = a et x + h = b
- x − y = a et h = b
- x + y = a et h = b
Il monte l'identité remarquable :
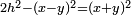 ; puis que, deux nombres étant donnés
; puis que, deux nombres étant donnés 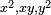 sont en progression géométrique. Il propose alors de vérifier que le triangle de base x − y, d'hypoténuse x + y et de hauteur
sont en progression géométrique. Il propose alors de vérifier que le triangle de base x − y, d'hypoténuse x + y et de hauteur 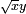 est rectangle.
est rectangle.Viète revient alors aux questions initiales ; sachant x,y et t, en progression géométrique ; il demande de les déterminer, pour a et b donnés, si :
- x = a et
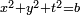
- x + t = a et
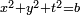
- y = a et
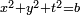
Viète fait remarquer au passage que dans ce cas :
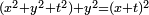
Il passe alors à des problèmes comportant quatre grandeurs continuellement proportionnelles (x,y,t,u tels que y = Ax,t = Ay,u = At) et propose de les déterminer pour a et b donnés, si
- x = a et
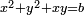
- u − x = a et t − y = b
- u + x = a et t + y = b
Aucune de ces questions n'a été soulevée par Diophante. Dans ce livre, Viète commence à accélérer ses démonstrations, ramenant chaque fois qu'il le peut la construction de l'exégétque ou la discussion poristique à un cas déjà vu antérieurement. On y lit des maths en marche et Viète semble réellement avoir conscience de la formidable machine à résoudre qu'il vient de créer.
Postérité
Les années Viète (1603-1646)
Outre Catherine de Parthenay et le turbulent Tarporley, Viète eut vraisemblablement quatre élèves : Jacques Aleaume d'Orléans, qui trouvera un poste de déchiffreur auprès de Maurice d'Orange ; un mathématicien célèbre, originaire de Raguse, Marin Ghetaldi, qui après quelques voyages retournera siéger au grand conseil de sa république natale ; Jean de Beaugrand, qui, après avoir été l'ami de Fermat, sera tourné en ridicule par Descartes et enfin, le mathématicien écossais Alexander Anderson. Ils illustreront ses théories en publiant ses œuvres et en continuant sa méthode. À sa mort, ses héritiers ont remis ses manuscrits entre les mains de Pierre Aleaume[24]. Ils passeront à son fils, puis, à sa mort, se perdront entre les mains des frères Dupuy. On donne ici les éditions posthumes les plus importantes.
- En 1612 : Supplementum Apollonii Galli de Marin Ghetaldi.
- De 1615 à 1619 : Animadversionis in Franciscum Vietam, a Clemente Cyriaco nuper par Alexander Anderson
dont Francisci Vietae Fontenaeensis de aequationum recognitione et emendatione tractatus duo per Alexandrum Andersonum. Paris, Laquehay, 1615, in 4, 135 p.
La mort d'Alexander Anderson ou celle de la fille de Viète interrompirent malheureusement cette publication.
En 1629, Albert Girard publie sa propre algèbre nouvelle, essentiellement numérique, dans laquelle il rend hommage à Viète.[109] en ces termes :
- Touchant François Viète, qui surpasse tous ses devanciers en l'algèbre, on peut voir en son traité (De recognitione equationium)...
mais lui reproche d'oublier dans ses résolutions les solutions négatives (moins que rien) et complexes (qu'il nomme enveloppées).
En 1630 est publiée une Introduction en l'art analytic ou nouvelle algèbre, traduite en notre langue et commentée par J.L. Sieur de Vau-Lezard, mathématicien. Paris, Jacquin, in 12, 79 p, ainsi que Les cinq livres des zététiques de François Viette, mis en français, commentés et augmentés, par J.L. Sieur de Vaulezard, mathématicien. Paris, Jacquin, 219 p."" Disponibles ici dans leur version de 1630. La même année parut un Isagoge sous la plume d'Antoine Vasset (assimilé un pseudonyme de Claude Hardy)[110] et l'année suivante une traduction en latin de Beaugrand dont Descartes aurait reçu un exemplaire[111].
En 1635, le mathématicien français James Hume de Godscroft, d'origine écossaise (connu pour ses polémiques avec Jean-Baptiste Morin) donne une Algèbre de Viète d'une méthode nouvelle et facile par laquelle toute l'obscurité de l'auteur est ôtée, qui marque la transition entre l'écriture de Viète et celle de Descartes, ainsi qu'un Traité de trigonométrie et un Traité relatifs aux sphères de Copernic et de Galilée[112] et un traité d'algèbre plus personnel (publié à Paris, en 1635) mais dans le droit fil de la logistique spécieuse.
En 1644, Noël Duret, cosmographe du roi, publie une algèbre nouvelle dite de Viète, mais dans la symbolique de James Hume et d'Harriot[113].
En 1646, le corpus des œuvres mathématiques de Viète est imprimé par Frans van Schooten, professeur à l'université de Leyde (presses des Elzevirs). Il est aidé dans son travail par Jacques Golius et par le Père Mersenne.
Les Anglais Thomas Harriot et Newton, le Hollandais Snellius, Huyghens et les Français Pierre de Fermat et Pascal utiliseront un temps les notations de Viète[114]. Plus tard, Leibniz, qui appréciait son héritage[115]cherche à faire en analyse ce que Viète à fait pour les équations[116] mais après 1649 et la réédition de la Géométrie de Descartes, sa renommée sera éclipsée par celle de du philosophe de la Haye, qui rénovera en profondeur ce formalisme, et auquel le siècle suivant attribuera souvent, à tort, l'entière paternité de la formalisation algébrique[117].
L'oubli et la reconnaissance
Vers 1730, il tombe quasiment dans l'oubli ; pour mémoire, Edmund Stone, dans sa préface historique à l'analyse des infiniments petits du Marquis de L'hôpital le cite trois fois, contre 28 pour Descartes[118]. En 1754 Jean François Dreux du Radier, érudit poitevin, donne une histoire très complète de sa vie, et notamment de la première disparition de l'Harmonicon Céleste entre les mains de Bouillaud[119].
Vers 1770, l'Italien Targioni Tozzetti, retrouve à Florence le manuscrit perdu de l'Harmonicum Céleste, œuvre de Viète, non publiée, où il affirme : « Describat Planeta Ellipsim ad motum anomaliœ ad Terram. » Cette ouvre laisse penser que Viète avait eu l'intuition de certaines théories de Kepler bien avant 1609)[120]. La décennie suivante, le nom de Viète est mentionné avec sympathie par l'abbé Sauri[121] mais De Paulmy d' Argenson [122] rend désormais hommage à son génie en trois lignes (sur 69 volumes).
En 1802, Charles Bossut, dans son histoire des Mathématiques, tente de redonner à Viète la paternité des premières applications de l'algèbre à la géométrie. Il écrit :
- Quelques auteurs ont imprimé, d'autres ont répété, et on répète tous les jours en conversation, que Descartes est l'inventeur de l'application de l'Algèbre à la Géométrie. Cela n'est pas exact. On accorde à Descartes plus qu'il ne doit prétendre, et on oublie trop les droits de ses prédécesseurs, et en particulier ceux de Viète[123].
En 1831, Joseph Fourier, dans son analyse des équations[124], mentionne Viète comme un des plus illustres mathématiciens, le second inventeur de l'algèbre, après Al Kwarizmi En 1837, le géomètre français Michel Chasles est l'un des premiers à réévaluer son rôle dans la mise en place de l'algèbre moderne, notamment dans Aperçu historique sur l'origine et le développement des méthodes en Géométrie[125]. Le 5 mai 1844, il lui rend hommage à l'académie des Sciences au travers d'une communication sur la nature des opérations algébriques.
En 1847, une lettre de François Arago, secrétaire perpétuel de l'académie des sciences, annonce son intention de tracer une biographie de François Viète[6].
Entre 1880 et 1890, le polytechnicien Frédéric Ritter, nommé en poste en Fontenay-le-Comte, reprend les traductions en français des œuvres de Viète. Il est son premier biographe contemporain avec Benjamin Fillon[126] Depuis de nombreuses études contemporaines (voir bibliographie) tendent à redonner toute son importance aux travaux du mathématicien des Parthenay, faisant ressortir qu'il eut le double mérite d'introduire les premiers éléments de calcul littéral et d'en forger une première axiomatique. Bien que Viète ne fut pas le premier à proposer de noter des quantités inconnues par des lettres (Jordanus Nemorarius l'avait déjà fait au XIIe siècle), ces études tendent à montrer qu'il serait réducteur de résumer ses innovations à cette seule découverte, et le situent à la charnière de la transformation algébrique opérée au cours de la fin XVIe - début XVIIe siècle[127].
Son influence sur Descartes
Trente quatre ans après la mort de Viète, le philosophe René Descartes publie avec le discours de la méthode un livre de géométrie qui bouleverse le paysage algébrique, amplifie l'algèbre de Viète[128], et la simplifie en ôtant ses exigences d'homogénéité. Descartes, accusé par Jean Baptiste Chauveau, un ancien condisciple de La Flèche, se défendra d'avoir lu Viète dans une lettre à Mersenne datée du 20 février 1639[129] :
« Je n’ai aucune connaissance de ce Géomètre dont vous m’écrivez, et je m’étonne de ce qu’il dit, que nous avons étudié ensemble Viète à Paris ; car c’est un livre dont je ne me souviens pas avoir seulement jamais vu la couverture, pendant que j’ai été en France. »S'il reconnaît ultérieurement l'avoir feuilleté, mais sans l'approfondir, il affirme avoir trouvé ses notations embrouillées et inutiles ses justifications géométriques. Dans quelques lettres, il montre qu'il a compris le programme de l'Arte Analyticem Isagoge. Dans d'autres, il caricature les propositions de Viète. Un de ses biographes notera cette contradiction :
« Ces derniers mots surprennent d'ailleurs ; car il [Descartes] venait de dire, quelques lignes plus haut, qu'il avait tâché de ne mettre, dans sa Géométrie, que ce qu'il croyait « n'avoir point été sceu ni par Viète, ni par aucun autre ». Il était donc au courant de ce que savait Viète ; et il avait dû le lire auparavant[130]. »En l'état actuel de la recherche, l'influence directe des œuvres de Viète sur Descartes n'est pas clairement établie. Elle a pu également se faire au travers d'Adrien Romain et de Jacques Aleaume à La Haye, ou par l'entremise du livre de Jean de Beaugrand, que ce dernier a fait passer par Mersenne et que Descartes a reçu le 3 mai 1632[131],[7]. On lira pour s'en convaincre les conclusions de Chikara Sasaki[132] mais aussi celle du père André[133]
Dans ses lettres à Mersenne, Descartes minimise consciencieusement l'originalité et la profondeur des travaux de ses prédecesseurs[134]. il commence, dit-il, par où Viète a fini. Son point de vue s'imposera au cours du XVIIe siècle et les mathématiciens y gagneront un langage algébrique dégagé de l'exigence de l'homogénéité[135].
Motivations d'une œuvre
Au-delà des nécessités de l'évolution des mathématiques, et des causes culturelles qui ont rendu possible l'émergence du calcul formel, il est chez Viète une préoccupation primordiale, qui se manifeste dans les dernières années de sa vie de façon poignante et qui articule ses études d'astronomie-géométrique et sa foi. Longtemps considéré comme protestant, voire parfois comme athée, puis comme politique, et enfin comme indifférent, le mathématicien résiste à la nomenclature et parvient à si bien brouiller les pistes qu'on ignore réellement aujourd'hui ses convictions en matière religieuse.
Protestant malgré lui ?
Viète a été accusé de protestantisme par les Ligueurs ; mais il n'est pas de témoignage certain qu'il fut huguenot. Son père s'est converti, et sans doute une bonne part de sa famille proche, mais parmi ses neveux, et ses cousins, ont compte autant de protestants que de catholiques. Dans la dédicace de son Isagoge (1591), il rend grâce à Catherine de Parthenay et à Françoise de Rohan de l'avoir sauvé de certains périls, qu'il ne précise pas, et qui ont accrédité la thèse de sa conversion. Était-il indifférent en matière religieuse ? Certaines invocations au très haut (contre Scaliger, en face de CLavius) laissent penser que non. Il semble toutefois qu'il n'ait pas adopté la foi calviniste des Parthenay, ni celle de ses autres protecteurs, les Rohan. Ou alors, fort brièvement. Sa nomination au parlement de Rennes l'atteste : lors de sa réception en tant que membre de la cour bretonne, le 6 avril 1574, il lit en public une profession de foi catholique (ce à quoi n'aurait pas consenti un huguenot convaincu, sinon sous la menace).
Néanmoins, Viète a défendu et protégé toute sa vie le parti des protestants et subi, en retour, les foudres des ligueurs. Il semble que, pour lui, la stabilité de l'État doive être préservée avant tout et, qu'au regard de cette exigence, la religion du Roi n'a pas d'importance. On le classe d'ordinaire parmi les « politiques », mouvement qui trouve ses racines dans la prudence de Michel de l'Hospital.
Pour aller plus loin, on a vu qu'à l'article de sa mort, il ne souhaitait pas se confesser et que le président Dolet l'en aurait convaincu, arguant que sa plus jeune fille ne trouverait aucun parti s'il refusait les sacrements de l'Église. La question de savoir si Viète était athée fut un temps débattue[136]. L'époque en comptait peu, et l'affirmation était lourde de conséquence; L'accusation envoyait au bûcher. Les seuls athées notoires de cette époque sont certains scientifiques de l'entourage du neuvième comte de Northumberland, dont Harriot faisait partie, mais on ne connaît pas de cas similaire pour la France.
L'évolution de sa cosmographie
Aujourd'hui, François Viète possède son cratère sur la Lune par 29,2 ° Sud et 56,3 ° Ouest[137]. Cela semble justice au regard de ses travaux en astronomie ; ses principes cosmographiques, un des manuels destinés à Catherine de Parthenay, montre qu'il s'y est intéressé très tôt. Sa pensée à ce sujet semble d'ailleurs avoir été très mobile. Dans ces premiers principes, Viète manifeste en effet une foi incontestable dans le système de Ptolémée. Il est certain qu'en milieu huguenot, aussi bien qu'en milieu catholique, l'héliocentrisme était mal vu.[138] Il en est arrivé avec son œuvre principale, l'Harmonicon Céleste, à un point de vue plus distant, équilibré et plus technique entre les théories de Ptolémée et de Copernic. Au moine et médecin Polonais, il reproche essentiellement d'être un mauvais géomètre. Il le fait avec une grande force dans les appendices qui suivent l'Apollonius Gallus[7].
L'histoire de cette œuvre dont on connaît un manuscrit[139] et plusieurs copies[140], tour à tour perdus puis retrouvés, mérite également qu'on l'évoque : à la mort de De Thou (en 1617), qui en conserve le manuscrit, sa splendide bibliothèque est dispersée. Un catalogue en est dressé par Bouillaud et les frères Dupuis (Bullialdus and Puteanus). Mais l'Harmonicon Céleste est envoyé par Ismael Bouillaud à Cosme de Médicis (1590-1621) et Bouillaud, feignant d'oublier à qui il l'a envoyé, ne fait pas figurer l'ouvrage au catalogue de la bibliothèque de De Thou (1645). Son existence est néanmoins divulguée par Sherburne, en 1675, qui évoque ce travail car il en a communiqué un exemplaire à Mersenne et n'a jamais pu le récupérer[141]. S'agit-il de l'exemplaire que retrouvent l'Italien Targioni Tozzetti, puis le comte Libri (dans la bibliothèque Magliabecchi de Florence) ? Au XIXe siècle, l'exemplaire de cet Harmonicon, est de nouveau égaré par le comte Libri avant de ressurgir au XXe siècle.
Toutefois, cette dernière œuvre n'étant pas publiée, il est difficile d'affirmer de combien d'années Viète a devancé Kepler dans la détermination de la forme elliptique des orbites des planètes, ni si Kepler l'a eu en main, ce que croit Grisard. Un résumé de cette « Harmonie Céleste » est donné par l'historien italien dans son histoire des sciences mathématiques[142]. On y apprend que Viète décrit correctement les orbites des planètes - celle de la terre exceptée -, c'est-à-dire qu'il les identifie à des ellipses, et non pas à des cercles, comme l'avait fait Copernic. Il ne semble pas pour autant - au vu de ce que Libri rapporte de cet ouvrage - que le mathématicien ait tranché entre les systèmes de Copernic et de Ptolémée. Cette intuition géométrique demeure cependant remarquable, et il faut sans doute ramener la prudence de Viète à publier de tels résultats au traitement que la papauté fait subir à Giordano Bruno le 17 février 1600.
L'idée que toute la trigonométrie sphérique de Viète et ses efforts de résolution algébrique étaient en fait tournés vers l'astronomie est une idée qui anime de nos jours la recherche[143]. L'évolution de son point de vue semble par ailleurs confirmé par les références que Viète fait aux Coperniciens dans ses écrits contre Clavius.
Notes
- ↑ Gaston Darboux (1902) : Éloges académiques suivi d'un éloge historique de Joseph Bertrand
- ↑ Foussais, la Bigotière : lieu de résidence ou lieu de naissance de Viète.
- ↑ a , b , c , d , e , f , g , h , i , j , k , l , m , n , o , p , q , r , s , t , u , v , w , x , y , z , aa , ab , ac , ad , ae , af , ag et ah Étude sur la vie du mathématicien François Viète (1540-1603), son temps et son œuvre, par Frédéric Ritter, polytechnicien et ingénieur des Ponts et Chaussées : tome I disponibles sous forme de microfilm (87Mi/1) auprès du CARAN
- ↑ Carilian-Gœury et Vor. Dalmont, éditeur Nouvelles annales de mathématiques: journal des candidats aux écoles polytechnique et normale
- ↑ Compte rendu Association française pour l'avancement des sciences
- ↑ a , b , c , d , e , f , g , h , i , j , k et l François Ritter François Viète fondateur de l'algèbre moderne dans la revue occidentale philosophique, sociale et politique (2d série, volume X). 1895
- ↑ a , b , c , d , e , f , g , h , i , j , k , l , m , n , o , p , q , r , s , t , u et v Jean Grisard, François Viète, mathématicien de la fin du seizième siècle : essai bio-bibliographique. Thèse de doctorat de 3e cycle, École pratique des hautes études, Centre de recherche d'histoire des sciences et des techniques, Paris, 1968; disponible au Centre Koyré Jardin des Plantes : Pavillon Chevreul 3e étage 57 rue Cuvier 75005
- ↑ Benjamin Fillon, Les maisons des hommes illustres de Fontenay, publié à Fontenay-le-Comte en 1848 in 8°
- ↑ Généalogie du mathématicien François Viète et de sa famille, par G. Gambier, 1931, 44 p. dact. disponibles sous forme de microfilm (fond Raspail : 106 AP 12) auprès du CARAN
- ↑ a , b , c , d , e , f , g , h , i , j , k et l Évelyne Barbin (dir.) et Anne Boye (dir.), François Viète, un mathématicien sous la Renaissance, Vuibert, 2005, (ISBN 2-7117-5380-8) disponible sur ici ou là.
- ↑ Doinel, Jules-Stanislas : Les registres des actes de la faculté de droit de Poitiers au XVIIe siècle in Bulletin de la Société de Statistique, Sciences et Arts du département des Deux-Sèvres, t. 1 (1870-1873) publié en 1871 à Niort
- ↑ Nicolas Rapin Œuvres ; publiées par la librairie Droz
- ↑ Matthew A. Vester, Jacques de Savoie-Nemours, sur le procès de Marie Stuart et ses conséquences : page 135
- ↑ a , b , c et d [pdf] Ritter, François Viète inventeur de l'algèbre moderne
- ↑ Matthew A. Vester, Jacques de Savoie-Nemours : l'apanage du Genevois au cœur de la puissance
- ↑ a et b [pdf] Ressources IREM
- ↑ Jules Bonnet, François Viète, Mémoires de la vie de Jean de Parthenay-Larchevêque, sieur de Soubise
- ↑ Manuscrits des mémoires de la Vie de Jean de Parthenay, Bibliothèque nationale, Fond Dupuy vol 743 folio 189-219
- ↑ Généalogie des maîtres de Requêtes de l'hôtel du roi depuis 1575 jusqu'à la moitié du XVIIIe siècle.
- ↑ [Mémoires de la Société des antiquaires de l'Ouest, volume 22, par Société des antiquaires de l'Ouest (Poitiers, France) page 475]
- ↑ Chronologie de la vie de François Viète
- ↑ Boucher d'Argis, Bibliothèque nationale, manuscrits Dupuy, vol 743, études postérieures à Viète mais non récentes N° 16 et 17.
- ↑ J. Mangis, Histoire du Parlement de Paris, 1906
- ↑ a , b , c , d , e et f Histoire universelle de Jacques-Auguste de Thou : depuis 1543. jusqu'en 1607, tome 14, livre CXXIX, p. 162-166
- ↑ Jean Bouhier, Traité de la dissolution du mariage pour cause d'impuissance avec quelques pièces curieuses sur le même sujet, 1735, chez Jean Marie Vander Kragt au Luxembourg. (Relation de ce qui s'est passé au sujet de la dissolution du mariage de Charles de Quellenec, baron du Pont, avec Catherine de Parthenay) : p. 185-237.
- ↑ Auguste François Louis du Roure, Analectabiblion
- ↑ Duc de Saint Simon, Mémoires
- ↑ Bernier Briquet, Dictionnaire historique, littéraire et bibliographique des Françaises
- ↑ Jean Baptiste Pierre Jullien de Courcelles, Dictionnaire historique et biographique des généraux français
- ↑ Hector de La Ferrière, Trois amoureuses au XVIe siècle. Françoise de Rohan - Isabelle de Limeuil - La Reine Margot, ISBN 1421256258, 9781421256252
- ↑ Pierre de L'Estoile Mémoires : Journal de Henri III ; publié 1825, copie de l'exemplaire Université d'Oxford, numérisé le 5 janvier 2007
- ↑ a et b Association française pour l'avancement des sciences Comptes rendus
- ↑ a et b Philippe Lenoir, Histoire ecclésiastique de Bretagne depuis la Réformation
- ↑ F. Saulnier, Le parlement de Bretagne, Rennes, 1909
- ↑ Archives du Parlement de Bretagne dans les archives de la cour d'appel de Rennes
- ↑ La Roche Flavien, Le Parlement de Bretagne, Rennes, 1909
- ↑ Eugène Haag, Émile Haag, La France protestante ; extraits de lettres de Henri de Navarre
- ↑ (en)J.V. Pepper Article à propos de la visite de Tarporley à Viète : dans le British Journal for the history of science (III, III, juin 1967, n°2
- ↑ (en)Annals of 1899, Schrewsbury school, page 60
- ↑ Franz Xaver Zach : Correspondance astronomique, géographique, hydrographique et statistique
- ↑ Prise du château de Blain sur le site d'Info-Bretagne
- ↑ Jean Moreau : Histoire de ce que s'est passé en Bretagne durant les guerres de la Ligue
- ↑ Les Cinq cents de Colbert, Bibliothèque Nationale
- ↑ Lavisse : Histoire de France illustrée depuis les origines jusque à la Révolution, Paris, 1911
- ↑ Décryptage automatique - code par substitution
- ↑ Stéphanie Félicité Genlis (comtesse de) : Histoire de Henri le Grand, Volume 1
- ↑ [pdf]Département de mathématiques et d’histoire des sciences Un exemple de déchiffrement 'à la Viète'
- ↑ (en)Friedrich Ludwig Bauer, Decrypted secrets: methods and maxims of cryptology
- ↑ Deux jugements signés par Viette (ou Viete), en décembre 1592, dans les archives de l'art français.
- ↑ Vie de Thomas Egrrlon, lord chancelier d'Angleterre, p. 329 et 330
- ↑ Michel Serfati, Dominique Descotes, Mathématiciens français du XVIIe siècle : Descartes, Fermat, Pascal
- ↑ Le site Apprendre en ligne François Viète, cryptanalyste du roi Henri IV
- ↑ Alexandre Savérien ,Jean-Charles François : Histoire des philosophes modernes, Volume 5
- ↑ Lettres Françaises de Joseph Scaliger, publiées par TH. de Larroque Paris 1887.
- ↑ Scaligae Epistolae, Leyde 1627
- ↑ Dominique Baudier : Litterae caturias tres, 4e éd. Amsterdam, 1639
- ↑ (de) Jean-Paul Delahaye L'histoire de Pi
- ↑ Librairie Droz : Methode et Theologie
- ↑ Cf.Sylvestre-François Lacroix et Jean-Etienne Montucla, Histoire des recherches sur la quadrature du cercle, Bachelier père et fils, 1831, p. 206.
- ↑ Denis Diderot L'Encyclopédie, tome 7, p 625
- ↑ [1]
- ↑ (en) Institut and museum of history of science Michel Coignet
- ↑ a et b Le Bibliophile belge : A. Ruland Adrien Romain, premier professeur de Wurzbourg
- ↑ (en)Henk J.M. Bos, « Descartes, Elisabeth and Apollonius’ Problem ». In The Correspondence of René Descartes 1643, Quæstiones Infinitæ, pages 202–212. Zeno Institute of Philosophy, Utrecht, édition de Theo Verbeek, Erik-Jan Bos et Jeroen van de Ven, 2003
- ↑ [pdf] Sébastien Maronne, La correspondance Sluse-Pascal et la Géométrie, sept. 2008, p 3.
- ↑ Cercles de Soddy
- ↑ Cercles de Soddy chez Wolfram
- ↑ P. Mathieu : histoire de France et des choses admirables survenues pendant les guerres, Paris 1605, chez Pierre Mettayer
- ↑ Actes du conseil d'actes sur le site du CNRS
- ↑ (en) Maseres a specimen of vieta's method of resolving algebraic equations by approximation, London, 1800, ex. au Bristish Museum
- ↑ Canones in kalendarium gregorianum perpetuum, Le calendrier grégorien à la manière de François Viète, transcription de Rodolphe Audette.
- ↑ Jean Dhombres, François Viète, l'homme qui voulut être roi du temps, dans Les Cahiers de Science et vie N° 60.
- ↑ (de)Die polemik über die Gregorianische Kalendereform (Wien 1877)
- ↑ Jérôme Delatour Noël le 15 décembre : la réception du calendrier grégorien en France (1582)
- ↑ Joël Biard, Sabine Rommevaux : Mathématiques et théorie du mouvement: XIVe-XVIe siècles
- ↑ (en)Knight, Charles: English cyclopaedia, a new dictionary of universal knowledge (Volume 6) 1791-1873
- ↑ Jacqueline A. Stedall,Thomas Hariot The greate invention of algebra: Thomas Harriot's treatise on equations
- ↑ (en)James Orchard Halliwell-Phillipps : A collection of letters illustrative of the progress of science in England
- ↑ Joseph Bertrand Éloges académiques
- ↑ Claude Barnard Petitot Collection complète des mémoires relatifs à l'histoire de France
- ↑ Tallemant Des Réaux, Louis-Jean-Nicolas Monmerqué, Paulin : Mémoires qui appartiennent à la collection de M. Feuillet de Couches dans Les Historiettes de Tallemant des Réaux, volume 1
- ↑ Note sur le chiffrement de Viète de Pereisc, Bulletin de la Société de l'histoire de France, 1853-1854, p 40.
- ↑ Hughes de Salins dans le Fonds Louis Morand Archives municipales de Beaune
- ↑ Benjamin Fillon lors des Séances générales de la Société française pour la conservation des monuments historiques (1846)
- ↑ Lettre de Jean Joguet, sous-archiviste aux Archives départementales de Charente-Maritime, adressée à Edgar Viette de La Rivagerie, 15 octobre 1956, et transcription dact. d’actes concernant la famille Viète et conservés aux Archives départementales de Charente-Maritime. Consultable aux [ http://www.archivesnationales.culture.gouv.fr/chan/chan/pdf/ap/apscient.pdf archives nationales (fond Raspail 106 AP 12) ]
- ↑ IREM de Rennes, Faire des mathématiques à partir de l'histoire, chap. 11, François Viète, section 11-3, Le Parlement de Bretagne.
- ↑ Maximilien Marie, Histoire des sciences mathématiques et physiques, t. III(1883), p 46.
- ↑ Michel Chasles : Aperçu historique sur l'origine et le développement des méthodes en gémoétrie
- ↑ Ritter Fr. La trigonométrie de François Viète
- ↑ Gergonne, Sorlin : Recherches en trigonométrie sphérique
- ↑ Kahn David, La Guerre des codes secrets, InterEditions, 1980, pp. 29-31
- ↑ Delahaye Jean-Paul, Viète, inventeur de la cryptanalyse mathématique, Pour la Science n° 313, novembre 2003, pp. 90-95
- ↑ Note de G. Bigourdan, Sur un ouvrage de F. Viète, supposé perdu, l'Harmonicon coeleste, Académie des sciences,14 fév. 1916.
- ↑ [pdf] Henri Bosmans, Le traité des sinus, de Michiel GOIGNET
- ↑ Voir note de Gérard Ferreyrolles et Philippe Sellier au tout début du traité de Pascal, De l'esprit géométrique, in Pascal. Les Provinciales. Pensées et opuscules divers, La Pochothèque, 2004, p.109
- ↑ (it) Opera de Galileo Galilei ed Nazionale t XVIII p 69 lettre de G.B. Baliani à Galilée le 1.
- ↑ Mahdi Abdeljaouad : Le manuscrit mathématique de Jerba
- ↑ Pierre Forcadel : L'Arithmétique de Rainer Gemma Frisius
- ↑ Tibor Klaniczay, Eva Kushner, Paul Chavy, L'époque de la Renaissance: 1400-1600, Volume 4
- ↑ Nicolas Bourbaki, Éléments d'histoire des mathématiques
- ↑ F. Ritter, Traduction française de la dédicace de 1591 de l'Introduction à l'Art analytique ou Algèbre Nouvelle, sur le site de Jean-Paul Guichard.
- ↑ Nicolas de Chamfort, Maximes et Pensées Des savants et des gens de lettres Chapitre VII, pensée CDXIX
- ↑ IREM de Rennes, Faire des mathématiques à partir de l'histoire, chap. 11, François Viète, section 11-2, Les Rohan.
- ↑ Voir en:Viète's formulas sur Wikipedia de langue anglaise
- ↑ Dominique Berlioz, Filipe Drapeau Contim, Un essai logique de Leibniz, « Le calcul des ingrédients »
- ↑ Michel Serfati, La révolution symbolique [détail des éditions] , chap VII, Viète et la dialectique de l'indéterminée.
- ↑ La mathématiques, les lieux, les temps, édition du CNRS, sous la direction de Claudio Bartocci et Piergiorgio Oldifreddi
- ↑ B. Lefebvre Cours développé d'Algèbre élémentaire paru chez A.Wesmael Charlier (Namur) 1897/1898
- ↑ Albert Girard Invention nouvelle en l'algèbre
- ↑ François Viète, Edition complète traduites en Français par Antoine Vasset
- ↑ (en)Chikara Sasaki, Descartes's mathematical thought, Springer, 2003, p 259.
- ↑ (en) (en) Roger A. Mason : Scots and Britons: Scottish political thought and the union of 1603
- ↑ L'algèbre de Viète par Noël Duret Bibliothèque Mazarine 30053 ou BNF V 20154
- ↑ Jean-Louis Gardies : Du mode d'existence des objets de la mathématique
- ↑ Victor Cousin : Lettre de Leibniz dans Fragments philosophiques, Volume 3
- ↑ Nicolas Boubaki, Éléments de mathématiques, Fonctions de la variables réelle, Springer, 2007, p 58.
- ↑ Léon Brunschvicg, Membre de l’Institut Descartes et Pascal lecteurs de Montaigne
- ↑ Edmund Stone, Castel (Louis-Bertrand, r.p.) : Analise des infiniment petits: comprenant le calcul integral dans toute son étenduë : avec son application aux quadratures, rectifications, cubatures, centres de gravité, de percussion, & c. de toutes sortes de courbes Chez J.-M. Gandouin, 1735
- ↑ Jean François Dreux du Radier : Bibliothèque historique, et critique du Poitou
- ↑ (en) Noel M. Swerdlow,The planetary theory of François Viète, Journal for the History of Astronomy, Vol. 6, p.185
- ↑ L'abbé Sauri : Cours complet de mathématiques: Calcul. Elemens de géométrie
- ↑ Marc Antoine René de Voyer de Paulmy d' Argenson Mélanges tirés d'une grande bibliothèque, Volume 26
- ↑ Charles Bossut, Histoire générale des Mathématiques période III page 288
- ↑ [pdf] Joseph Fourier Analyse des équations (page 5 de la préface et 8 de l'introduction)
- ↑ Michel Chasles, Aperçu historique sur l'origine et le développement des méthodes en géométrie, M. Hayez, 1837, p 52 et suivantes.
- ↑ Benjamin Fillon Inventaire des Autographes et Des Documents Historiques
- ↑ Le symbolisme mathématique : l'usage des lettres, sur le site math 93.
- ↑ Ernst Hairer,Gerhard Wanner : L'analyse au fil de l'histoire
- ↑ Descartes, Lettre au père Mersenne, 20 février 1639.
- ↑ Charles Adam, Vie et œuvre de Descartes, Paris, L Cerf, 1910, p 215.
- ↑ C. de Waard, Descartes, Lettre à Mersenne du 2 mai 1632 Tome III page 296.
- ↑ (en)Chikara Sasaki, Descartes's mathematical thought, Springer, 2003, pp 246-274.
- ↑ Le Père André : documents inédits pour servir à l'histoire philosophique
- ↑ Jacqueline A. Stedall, The Greate Invention of Algebra : Thomas Hariot
- ↑ Université de Nantes, AFAS : Sommaire d'une esquisse biographique de Ritter sur Viète.
- ↑ Jean Dhombres, François Viète et la réforme sur le site de Jean-Paul Guichard.
- ↑ (en) Image du cratère Vieta : par John Edward Westfall Atlas of the lunar terminator, cratère Vieta
- ↑ Luther s'était élevé contre ceux qui soutenaient le mouvement de la terre ; Melanchthon avait repoussé le système de Copernic : dans La question de Galilée, les faits et leurs conséquences ; Henri Charles E L 'Épinois, Henri de L 'Epinois (1878)
- ↑ L'Harmonicon céleste, manuscrit de François Viète à la bibliothèque Magliabechiana classe XI N° 36
- ↑ L'Harmonicon céleste, manuscrit de François Viète à la bibliothèque Nationale (BNF)7274, fonds latin et 3282 fonds français
- ↑ (en) Augustus de Morgan A budget of paradoxes.
- ↑ Guillaume Libri, histoire des sciences mathématiques en Italie : depuis la renaissance des lettres jusqu'à la fin du XVIIe siècle Tome 4.
- ↑ Giovanna Cifoletti, Les usages astronomiques de l’algèbre entre les XVIe et XVIIe siècles
Voir aussi
Bibliographie
- François Viète, inventeur de l'algèbre moderne : sa vie, son temps, son œuvre. [Tome I] / Frédéric Ritter. - 1953 - 162 p. : ill. ; 33 cm. Copie dactylographiée faite d'après le manuscrit de la bibliothèque de l'Institut par E. Viette de La Rivagerie, 1953. - à consulter ici
- Collectif (Sir Michael F. Atiyah, Alain Connes, Freeman J. Dyson, , David Mumford), La Mathématique, les temps et les lieux, CNRS Éditions, Paris, 2009.
- Gaston Godard, François Viète (1540-1603), père de l'algèbre moderne, université de Paris-VII, France, Recherches vendéennes (ISSN 1257-7979);
- Évelyne Barbin (dir.) et Anne Boye (dir.), François Viète, un mathématicien sous la Renaissance, Vuibert, 2005, (ISBN 2-7117-5380-8);
- Jean-Paul Guichard et Jean-Pierre Sicre, « François Viète. Un juriste mathématicien » in Aventures scientifiques. Savants en Poitou-Charentes du XVIe au XXe siècle (J. Dhombres, dir.), Les éditions de l’Actualité Poitou-Charentes, Poitiers, 1995, (ISBN 2-911320-00-X), p. 222-235;
- François Viète, Opera Mathematica, rassemblées par F. Van Schooten. Leyde, Elzévir, 1646, 554 p réédité par Georg Olms Verlag, Hildesheim-New York, 1970;
- Jean Grisard, François Viète, mathématicien de la fin du seizième siècle : essai bio-bibliographique. Thèse de doctorat de 3e cycle, École pratique des hautes études, Centre de recherche d'histoire des sciences et des techniques, Paris, 1968;
- Joël Biard, Rushdī Rāshid, Descartes et le Moyen Âge, Centre national de la recherche scientifique, Vrin, 1997,(ISBN 2711613402), [lire en ligne];
- (en) Michael Sean Mahoney, The mathematical career of Pierre de Fermat, 1601-1665, Princeton University Press, 1994, (ISBN 0691036667), [lire en ligne], Viet's analytic program;
- Sur Jacques Allaume et la pensée de Descartes : (en) Chikara Sasaki, Descartes's mathematical thought
- Frédéric Saulnier, 1909, Le Parlement de Bretagne (1554-1790), Repertoire alphabetique et biographique de tous les membres de la Cour, accompagne de listes chronologiques et precede d'une introduction historique. Imprimerie de la Manutention, Mayenne, réédition 1991.
- Dictionnaires des familles de l’Ancien Poitou publiés par Beauchet-Filleau, 1840-1979 dans les Archives départementales de la Vendée | Société d'émulation de la Vendée
- Jacques Bouveresse, Jean Itard, Émile Sallé, Histoire des mathématiques [détail des éditions]
Articles connexes
- Famille Parthenay et Rohan
- Michelle de Saubonne • Jean V de Parthenay • Antoinette d'Aubeterre • Catherine de Parthenay • Françoise de Rohan • Charles de Quellenec
- Prédécesseurs
- Apollonius de Perga • Théon d'Alexandrie • Meton • Albetagni • Jordan Nemorarius • Regiomontanus • Rheticus
- Contemporains
- Pierre de la Ramée • Guillaume Gosselin • Jacques Pelletier du Mans • Jamet Mettayer • Philippe van Lansberge • William Oughtred • Thomas Harriot • Michel Coignet • Ludolph van Ceulen • Simon Stevin • Le sieur de Vaulezard
- Successeurs
- Albert Girard • Pierre de Fermat • James Hume • Claude Hardy • Frans Van Schooten
- Élèves et amanuensis
- Pierre Aleaume et Jacques Aleaume • Charles du Lys • Tarporley • Marin Ghetaldi • Alexander Anderson • Jean de Beaugrand
- Contradicteurs
- Juste Scaliger • Adrien Romain • Clavius
- Ils l'ont sorti de l'ombre/Biographes
- François Arago • Michel Chasles • Guillaume Libri • Benjamin Fillon • Frédéric Ritter
- Pages mathématiques
- Chronologie de l'algèbre • Algèbre nouvelle • Problème d'Apollonius • Théorème de Descartes • Cercle d'Apollonius
Liens externes
Le corpus intégral (hormis l'harmonicon) des œuvres mathématiques de Viète fut imprimé bien après sa mort par Frans van Schooten, professeur à l'université de Leyde. Cette édition en un volume porte le titre Francisci Vietæ. Opera mathematica, in unum volumen congesta ac recognita, opera atque studio Francisci a Schooten, Officine de Bonaventure et Abraham Elzevier, Leyde, 1646 Texte en ligne On consultera également :
Site de Jean-Paul Guichard • L'algèbre nouvelle • Biographie par l'IREM de Rennes • Analyse sur Les Zeteticorum LIibri Quinque de Viète • La définition de littré • Article Viète de l'Universalis • Page:Diderot - Encyclopedie 1ere édition tome 1 • histoire de chiffres • Nouvelle page de Bibmath • Chronomath • Collège Albert Camus de l'Académie de Strasbourg • (en) La bibliographie de l'université de Saint Andrews • Notaires de Vendée • La bibliothèque du dix-septiémiste du Centre international Blaise-Pascal
- Portail des mathématiques
- Portail du protestantisme
- Portail de la cryptologie
Catégories : Bon article | Mathématicien français | Cryptologue | Personnalité du Bas-Poitou | Naissance en 1540 | Naissance à Fontenay-le-Comte | Décès en 1603
Wikimedia Foundation. 2010.