Trisection de l'angle

La trisection de l'angle est un problème classique de mathématiques. C'est un problème géométrique, faisant partie des trois grands problèmes de l'Antiquité, avec la quadrature du cercle et la duplication du cube. Ce problème consiste à diviser un angle en trois parties égales, à l'aide d'une règle et d'un compas.

Impossibilité générale avec la règle et le compas

S'il est facile de partager un angle en deux en construisant sa bissectrice, s'il est aisé de partager l'angle droit en trois à l'aide de triangles équilatéraux, beaucoup de mathématiciens ont longtemps cherché, en vain, une méthode géométrique pour réaliser la trisection d'un angle quelconque à la règle et au compas. Dès le III^e siècle av. J.‑C., Archimède proposa une méthode par ajustement (ou neusis), à l'aide d'un compas et d'une règle dotée de deux graduations. Au II^e siècle av. J.‑C., Nicomède utilisa une courbe auxiliaire, la conchoïde de droite pour déterminer la solution.

Mais en 1837, Pierre-Laurent Wantzel démontra le théorème qui porte son nom, permettant d'exhiber une large famille d'équations de problèmes impossibles à résoudre à la règle et au compas. L'équation de la trisection de l'angle étant de cette forme, la construction générale est donc impossible à réaliser selon ces règles. La trisection de l'angle est en revanche réalisable au moyen du compas et de la règle graduée, ou au moyen de courbes auxiliaires dites trisectrices, ou au moyen de pliage d'une feuille de papier.

Utilisation du compas et de la règle graduée

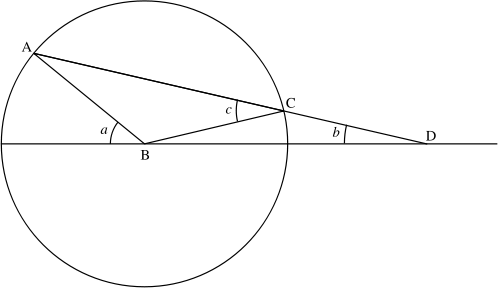
Archimède donne la construction suivante par ajustement, à l'aide d'un compas et d'une règle portant deux graduations. Soit a l'angle à trisecter, de sommet B. On trace un cercle de centre B et de rayon la distance séparant les deux graduations de la règle (soit r). Le cercle coupe l'un des côtés de l'angle en A (donc AB = r). On dispose la règle de façon à ce qu'elle passe par A, que l'une des graduations C de la règle soit disposée sur le cercle, et l'autre graduation D soit sur le prolongement (BD) de l'autre côté de l'angle (donc CD = r). L'angle b de sommet D est alors le tiers de l'angle a.

En effet, le triangle BCD est isocèle en C, donc l'angle CBD est égal à b. Mais dans le cercle de centre C passant par B et D, l'angle au centre ACB (= c) est le double de l'angle inscrit CDB (= b), soit c = 2b. Or BAC est également un triangle isocèle en B, donc l'angle BAC est égal à c. L'angle ABC vaut donc π − 2c = π − 4b. L'angle ABD vaut alors π − 3b, de sorte que l'angle a vaut bien 3b.

Utilisation de courbes trisectrices

Construction par pliage de papier

Voici une construction par origami due à Hisashi Abe (1980), qu'illustre la figure ci-contre :

• On trace la droite d passant par le coin A de la feuille de sorte qu'elle forme, avec le bord inférieur h₀ de la feuille, l'angle à couper en trois.
• Par pliage on détermine deux bandes horizontales de même largeur (arbitraire) en bas de la feuille. On appelle h₁ et h₂ les droites qui les délimitent.
• On plie la feuille le long d'un pli p de sorte que AB vienne en A'B' tel que le point A aille sur la droite h₁ (en un point A'), en même temps que le point B (intersection du bord gauche avec la droite h₂) ira sur la droite d en un point B' (axiome 6 des mathématiques des origamis).
• La droite t passant par A et A' est alors la trisectrice de l'angle donné: l'angle formé par h₀ et t vaut 1/3 de l'angle formé par h₀ et d.

La démonstration est simple : par symétrie par rapport à la droite p, le milieu P de AB donne le milieu P’ de A’B’ et, de même que A’P est perpendiculaire à AB, on a AP’ qui est perpendiculaire à A’B’. Les deux triangles rectangles P’A’A et P’B’A sont donc égaux.

D’autre part soit H la projection orthogonale de A’ sur h₀. Puisque les triangles HAA’ et PA’A sont égaux comme moitiés d’un même rectangle et que les triangles PA’A et P’AA’ sont aussi égaux par symétrie par rapport à p, il en résulte que les triangles HAA’ et P’AA’ sont égaux.

Par conséquent l'égalité des trois triangles HAA', P'AA' et P'AB' montre que les segments AP’ et AA’ partagent bien l’angle dAh₀ en trois angles égaux.

Voir aussi

Bibliographie

• Jean Aymes, Ces problèmes qui font les mathématiques (la trisection de l'angle), Association des professeurs de mathématiques de l'enseignement public, coll. « Publication de l'APMEP » (n^o 70), 1988, 100 p. (ISBN 2-902680-46-5) (OCLC 462328692) .
• (en) Roger C. Alperin, « Trisections and totally real origamis », dans Amer. Math. Monthly,, vol. 112, n^o 3, mars 2005, p. 200-211 .
• (en) Andrew M. Gleason, « Angle trisection, the heptagon, and the triskaidecagon », dans Amer. Math. Monthly, vol. 95, n^o 3, mars 1998, p. 185-194 .

Articles connexes

• Duplication du cube
• Nombre constructible
• Histoire de la géométrie
• Tour d'extensions quadratiques

• Portail de la géométrie