Probleme des contacts

Sommaire 1 Traité des contacts d'Apollonius 1.1 Lien externe 2 Constructions de tangentes et de cercles tangents 2.1 Tangente en un point du cercle 2.2 Tangentes à un cercle passant par un point donné 2.3 Cercle tangent à deux droites passant par un point donné 2.4 Cercle tangent à deux cercles 2.5 Lien externe

Traité des contacts d'Apollonius

Le problème des trois cercles : Trouver un cercle tangent à trois cercles donnés de rayons différents.

C'est un des grands problèmes de l'antiquité.

Ce problème dit problème d'Apollonius, a été présenté par Pappus comme étant le dixième et le plus difficile du Traité des contacts, un des ouvrages perdus d'Apollonius.

En effet, il faudra attendre 1600 pour sa résolution par François Viète qui montrera qu'il admet au maximum huit solutions.
Pour cela dans l'Apollonius Gallus, il va résoudre les dix problèmes présentés ci-dessous (sans traiter les cas particuliers).

La détermination de cercle astreint à trois conditions prises parmi celles qui consistent à passer par un point donné, ou à être tangent à une droite ou un cercle donné, répond à dix problèmes désignés par les symboles PPP, DDD, PPD, PPC... en représentant un point par P, une droite par D et un cercle par C.

• Le problème 1, PPP, est résolu avec le cercle circonscrit dont le centre est le point d'intersection des médiatrices du triangle.
• Le problème 2, DDD, a pour solutions les cercles inscrit et exinscrits lorsque les droites forment un triangle. Viète le traitera de façon isolée.
• Le problème 3, PPD, se ramène au problème 1 en utilisant des angles inscrits.
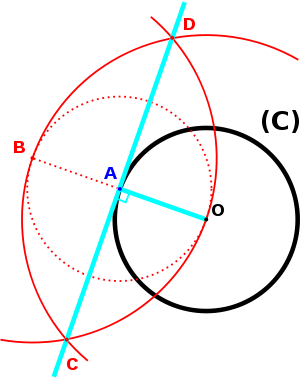
• Le problème 4, PPC, se trouve grâce à l'introduction d'un cercle intermédiaire.
• Le problème 5, PDD, se ramène au problème 4 en introduisant le symétrique du point par rapport à une bissectrice des deux droites.
• Le problème 6, PCC, se ramène au problème 4 en trouvant un deuxième point situé sur la droite joignant le point donné à un des centres de similitude des deux cercles.
• Le problème 7, PDC, se ramène au problème 3 grâce à un point intermédiaire
• Le problème 8, DDC, se ramène au problème 5 par la méthode des translations en déplaçant les droites d'une longueur égale au rayon du cercle.
• Le problème 9, DCC, se ramène au problème 7 en remplaçant le plus grand des cercles par un cercle ayant pour rayon la somme ou la différence des rayons de ces deux cercles et l'on déplace la droite parallèlement à elle-même d'une longueur égale au rayon du petit cercle.
• Le problème 10, CCC, se ramène au problème 6 en substituant aux deux plus grands cercles, des cercles concentriques dont les rayons différent d'une quantité égale au rayon du plus petit cercle.

Le problème sera généralisé par Descartes en 1643.

Lien externe

Construction de cercles

Constructions de tangentes et de cercles tangents

Trouver des points de contact - Utilisations de configurations faisant intervenir l'homothétie (deux droites) ou l'inversion (deux cercles).

Tangente en un point du cercle

D'un point A situé sur un cercle de centre O on peut mener une tangente à ce cercle en traçant la perpendiculaire en A au rayon [OA].

Construction à la règle et au compas (sans équerre). Tracer le point B symétrique de O par rapport à A et puis la médiatrice de [BO].

Tangentes à un cercle passant par un point donné

D'un point M extérieur à un cercle, on peut mener deux tangentes à ce cercle ; elles touchent le cercle en A et B et on a MA = MB. La droite (OM) est un axe de symétrie de la figure, c'est la bissectrice de l'angle AMB.

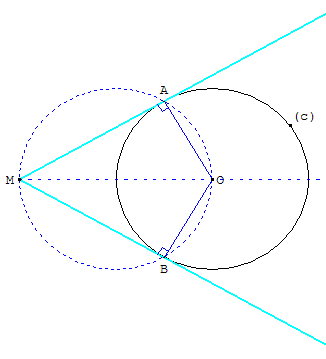
Construction d'Euclide

Étant donné un cercle (c) de centre O et un point M à l'extérieur du cercle, les points de contact A et B des tangentes issues de M sont les points d'intersection du cercle (c) et du cercle de diamètre [MO].

Cercle tangent à deux droites passant par un point donné

On donne deux droites (d₁), (d₂) sécantes et un point A n'appartenant pas à ces droites. Existe-t-il un cercle passant par A tangent à ces deux droites ?

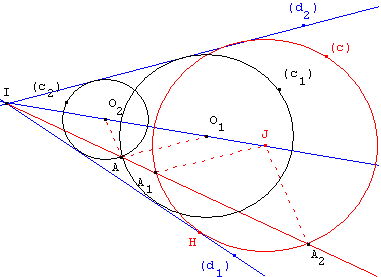
Construction

Placer un point J sur la bissectrice de (d₁, d₂) située dans le même secteur angulaire que le point A et tracer le cercle (c), passant par H projection orthogonale de J sur la droite (d₁). Ce cercle est tangent aux deux droites.

Étant donné un cercle (c), la droite (IA) rencontre (c) en deux points A₁ et A₂. La droite parallèle à (A₁J) passant par A rencontre (IJ) en O₁. Le cercle (c₁), de centre O₁ passant par A, est tangent à (d₁) et (d₂).

De même, la droite parallèle à (A₂J) passant par A rencontre (IJ) en O₂. Le cercle (c₂), de centre O₂ passant par A, est la deuxième solution du problème.

Cercle tangent à deux cercles

On donne deux cercles (c₁), (c₂) de centres O₁, O₂, de rayons différents r₁ et r₂. Étudier les cercles (c) tangents à ces deux cercles ?

Il existe deux homothéties H(S, r₁/r₂) et H(S', -r₁/r₂) transformant (c₁) en (c₂).

Les points S et S' centres d'homothéties des cercles sont les points qui partagent le segment [O₁O₂] dans le rapport r₁/r₂.

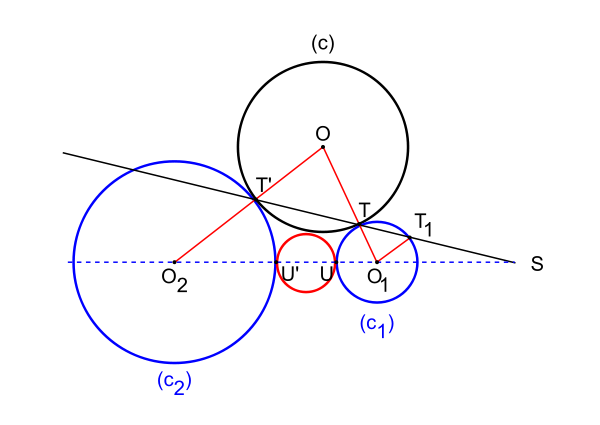
Si un cercle (c) est tangent aux cercles (c₁), (c₂) en T et T', la droite (TT') qui joint les points de contact passe par un centre d'homothétie. La puissance p du centre d'homothétie par rapport au cercle (c) variable est constante.

p = ST × ST' = ST × ST₁ × ST'/ST₁ = ST × ST₁ × r₂/r₁.

On obtient la puissance du pointS par rapport au cercle (c₁) multiplié par le rapport des rayons. Si U et U' sont les points d'intersection de (c₁) et (c₂) avec la ligne des centres, la puissance du point S par rapport au cercle de diamètre [UU'] est p = SU × SU'.

Le cercle (c) est globalement invariant par l'inversion de centre S de puissance p.

Lien externe

• (fr) Point d'Apollonius

• Portail de la géométrie