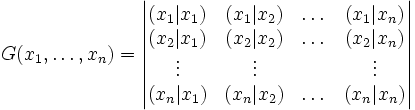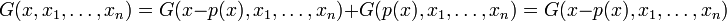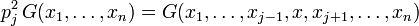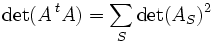Matrice de Gram

Déterminant de Gram

En géométrie euclidienne ou hilbertienne, le déterminant de Gram permet de calculer des volumes et de tester l'indépendance linéaire d'une famille de vecteurs. Il associe des calculs de produits scalaires et d'un déterminant. Son nom est un hommage au mathématicien danois Jørgen Pedersen Gram (1850-1916).

L'article déterminant montre comment définir le volume orienté d'un parallélotope formé par n vecteurs en dimension n, sans nécessité de munir l'espace d'un produit scalaire. Les déterminants de Gram demandent de définir un tel produit scalaire, permettent le calcul des volumes des parallélotopes de toutes dimensions, mais sans notion d'orientation.

Plus généralement, il est possible de calculer des déterminants de Gram sur un espace quadratique. En dimension finie, le discriminant d'une forme bilinéaire symétrique est un cas particulier de déterminant de Gram.

Sommaire

1 Définition
2 Interprétation géométrique
- 2.1 Calcul des volumes de parallélotopes
- 2.2 Application de la formule de Binet-Cauchy

Définition

Soit E un espace préhilbertien réel. Si x₁,..., x_n sont n vecteurs de E, la matrice de Gram associée est la matrice symétrique de terme général (x_i|x_j). Le déterminant de Gram est le déterminant de cette matrice

$G(x_1,\dots, x_n)=\begin{vmatrix} (x_1|x_1) & (x_1|x_2) &\dots & (x_1|x_n)\\ (x_2|x_1) & (x_2|x_2) &\dots & (x_2|x_n)\\ \vdots&\vdots&&\vdots\\ (x_n|x_1) & (x_n|x_2) &\dots & (x_n|x_n)\end{vmatrix}$

Propriétés

Écriture à l'aide d'une matrice représentative

Soit B une base orthonormale de l'espace engendré par les x_i ; elle contient 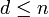$d\leq n$ vecteurs. Soit X la matrice représentative du système de vecteurs x_i dans B. C'est une matrice de taille 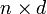$n\times d$ , dont chaque colonne contient les composantes d'un des vecteurs x_i. La matrice de Gram n'est autre que X ^tX.

Effet d'opérations élémentaires

la multiplication d'un des vecteurs par le réel a provoque une multiplication du déterminant de Gram par a²
le déterminant de Gram est invariant par permutation des x_i
l'ajout à un vecteur d'une combinaison linéaire des autres vecteurs laisse invariant le déterminant de Gram

Propriétés

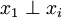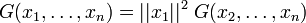
si $x_1\perp x_i$ pour tout $i\in[\![2,n]\!]$ , alors on a $G(x_1,\dots, x_n)=||x_1||^2\;G(x_2,\dots, x_n)$
le déterminant de Gram d'une famille de n vecteurs est toujours positif
il est nul si et seulement si la famille est liée

Démonstration

Si la famille est liée, 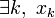$\exists k,\ x_k$ est combinaison linéaire des autres x_i ; donc

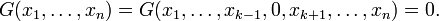
$G(x_1,\dots, x_n)=G(x_1,\dots,x_{k-1},0,x_{k+1},\dots, x_n)=0.$

Si la famille est libre, alors d=n, X est une matrice carrée inversible comme matrice de passage d'une base à une autre. Le déterminant de Gram est

(det X) 2

qui est strictement positif.

Application à la distance d'un vecteur à un sous-espace vectoriel

Soit F un sous-espace vectoriel de dimension finie n de E . Soient x₁,..., x_n, n vecteurs formant une base de F. Tout vecteur x de E admet un projeté orthogonal p(x) sur F.

On a : x=x-p(x)+p(x). Or p(x) est combinaison linéaire des x_i donc :

$G(x,x_1,\dots, x_n) = G(x-p(x), x_1, \dots, x_n) + G(p(x),x_1,\dots, x_n) = G(x-p(x), x_1, \dots, x_n)$

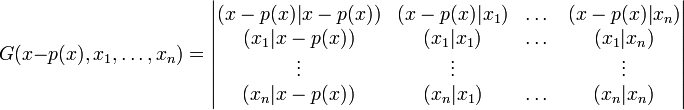
Puis : $G(x-p(x),x_1,\dots, x_n)=\begin{vmatrix} (x-p(x)|x-p(x)) & (x-p(x)|x_1) &\dots & (x-p(x)|x_n)\\ (x_1|x-p(x)) & (x_1|x_1) &\dots & (x_1|x_n)\\ \vdots&\vdots&&\vdots\\ (x_n|x-p(x)) & (x_n|x_1) &\dots & (x_n|x_n)\end{vmatrix}$

Mais x-p(x) est par définition orthogonal aux x_i, donc :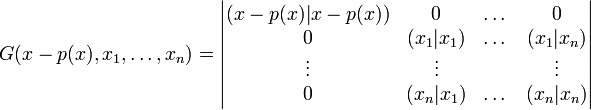 $G(x-p(x),x_1,\dots, x_n)=\begin{vmatrix} (x-p(x)|x-p(x)) & 0 &\dots & 0\\ 0 & (x_1|x_1) &\dots & (x_1|x_n)\\ \vdots&\vdots&&\vdots\\ 0 & (x_n|x_1) &\dots & (x_n|x_n)\end{vmatrix}$

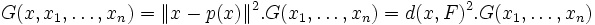
Ainsi : $G(x,x_1,\dots, x_n) = \|x-p(x)\|^2.G(x_1, \dots, x_n)=d(x,F)^2.G(x_1, \dots, x_n)$

Application au calcul des composantes d'un vecteur dans une base quelconque

Soit F un sous-espace vectoriel de dimension finie n de E, muni d'une base 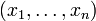$(x_1,\ldots,x_n)$ . Soit $x\in F$ .

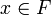On pose 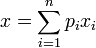$x = \sum_{i=1}^n p_i x_i$ . Alors pour tout $j\in[\![1,n]\!]$ on a la relation

$p_j^2\,{G(x_1, \dots, x_n)} = G(x_1, \dots, x_{j-1},x,x_{j+1}, \dots, x_n)$

Il ne reste plus qu'à trouver le signe de chaque $p j$

Interprétation géométrique

Calcul des volumes de parallélotopes

Le calcul de la distance à un sous-espace permet de montrer par récurrence que le déterminant de Gram d'une famille de n vecteurs est égal au carré du volume euclidien du parallélotope correspondant.

Pour n=1 c'est bien le cas car $G(x)=\|x\|^2$ .

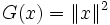En supposant la propriété vraie pour toute famille de n vecteurs, on l'établit pour n+1. La distance de x_n+1 à F espace engendré par les n premiers vecteurs est le carré de la hauteur du parallélotope, et G(x₁, ..., x_n) est le carré du volume de la base par hypothèse de récurrence.

Le volume s'obtient donc en prenant la racine carrée du déterminant de Gram, sans qu'il soit possible de lui donner un signe (pour plus de détails sur cette dernière question, consulter l'article orientation).

Application de la formule de Binet-Cauchy

La formule de Binet-Cauchy montre comment le volume d'un parallélotope de dimension d dans un espace de dimension n peut être ramené au calcul de volumes de projections orthogonales du parallélotope sur des sous-espaces de coordonnées. Elle s'écrit

$\det(A\,{}^tA) = \sum_S \det(A_S)^2\,$

dans cette expression S décrit les différents sous-ensembles à d éléments de l'ensemble { 1, ..., n }. Pour chaque S, la matrice A_S est la matrice carrée de taille d obtenue en ne retenant que les colonnes de A dont l'indice appartient à S.

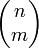La formule de Binet-Cauchy montre que le carré du volume du parallélotope est égal à la somme des carrés des volumes des projections orthogonales sur les différents sous-espaces de coordonnées de dimension m (qui sont au nombre de $\begin{pmatrix}n\\m\end{pmatrix}$ ).

Dans le cas m=1, ces projections orthogonales sont des segments, et on retrouve une forme du théorème de Pythagore.

Articles en rapport avec les matrices
Par forme	carrée • triangulaire • diagonale • tridiagonale • élémentaire • échelonnée • creuse • aléatoire • circulante • de Hankel • de Toeplitz • de Vandermonde
Transformée	transposée • adjointe • inverse • Comatrice
En relation	équivalente • semblable • congruente
Par propriété	inversible • diagonalisable • trigonalisable • symétrique • antisymétrique • hermitienne • normale • orthogonale • unitaire • symplectique • de Hadamard • définie positive • à diagonale dominante • nilpotente
Par famille	identité • de De Casteljau • de Cartan • de Hilbert • de Mueller • de Pauli • de Dirac
Particulière	CKM
Associée	de permutation • de passage • compagnon • de Sylvester • d'adjacence • laplacienne • hessienne • jacobienne • génératrice • de contrôle • de corrélation • de Gram • de variance-covariance • d'inertie • de Jones • des gains • stochastique
Résultats	décompositions : LU • QR • polaire • valeurs singulières Trigonalisation • Réduction de Jordan • facteurs invariants
Voir aussi	Théorie des matrices • Algèbre linéaire

Articles de mathématiques en rapport avec l'algèbre bilinéaire

Espace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice définie positive • Matrice semi-définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz

modifier

Portail des mathématiques

Ce document provient de « D%C3%A9terminant de Gram ».

Catégories : Algèbre bilinéaire | Déterminant

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice de Gram de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Matrice Définie Positive — En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif. On introduit tout d abord les notations suivantes ; si a est une matrice à éléments réels ou complexes : aT désigne la… … Wikipédia en Français
Matrice definie positive — Matrice définie positive En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif. On introduit tout d abord les notations suivantes ; si a est une matrice à éléments réels ou… … Wikipédia en Français
Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice De Hilbert — En algèbre linéaire, la matrice de Hilbert est une matrice carrée de terme général Bij = 1 / (i + j − 1). Elle est nommée ainsi en hommage au mathématicien David Hilbert. Les matrices de Hilbert servent d exemples classiques de matrices mal… … Wikipédia en Français
Matrice de hilbert — En algèbre linéaire, la matrice de Hilbert est une matrice carrée de terme général Bij = 1 / (i + j − 1). Elle est nommée ainsi en hommage au mathématicien David Hilbert. Les matrices de Hilbert servent d exemples classiques de matrices mal… … Wikipédia en Français
Matrice définie positive — En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif : une matrice définie positive est une matrice positive inversible (la réciproque est fausse). On introduit tout d abord les… … Wikipédia en Français
Matrice (mathématiques) — Pour les articles homonymes, voir Matrice. En mathématiques, les matrices sont des tableaux de nombres qui servent à interpréter en termes calculatoires et donc opérationnels les résultats … Wikipédia en Français
Matrice de Hilbert — En algèbre linéaire, la matrice de Hilbert est une matrice carrée de terme général Bij = 1 / (i + j − 1). Elle est nommée ainsi en hommage au mathématicien David Hilbert. Les matrices de Hilbert servent d exemples classiques de matrices mal… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Matrice de Gram

Déterminant de Gram

Sommaire