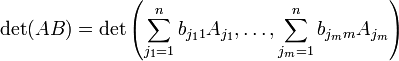Formule De Binet-Cauchy

Formule de Binet-Cauchy

Pour les articles homonymes, voir Cauchy et Binet.

En algèbre linéaire, la formule de Binet-Cauchy généralise la propriété de multiplicativité du déterminant d'un produit au cas de deux matrices rectangulaires. On peut l'écrire pour des matrices dont les coefficients sont dans un corps, ou plus généralement dans un anneau commutatif.

Énoncé

Pour pouvoir effectuer le produit des matrices A et B, on suppose qu'elles sont de tailles respectives m par n et n par m. La formule de Binet-Cauchy s'énonce alors

$\det(AB) = \sum_S \det(A_S)\det(B_S)\,$

dans cette expression S décrit les différents sous-ensembles à m éléments de l'ensemble { 1, ..., n }. Pour chaque S, la matrice A_S est la matrice de taille m obtenue en ne retenant que les colonnes de A dont l'indice appartient à S. De même B_S est la matrice de taille m obtenue en ne retenant que les lignes de B dont l'indice appartient à S.

Dans le cas où m=n, les matrices A et B sont carrées, il y a un seul terme dans la formule de Binet-Cauchy, qui redonne bien la propriété de multiplicativité des déterminants.

Si m > n, il n'y a pas d'ensemble S convenable et le déterminant de AB est nul, selon les conventions usuelles sur les sommes vides.

Si m < n, la formule demande d'effectuer la somme de 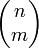$\begin{pmatrix}n\\m\end{pmatrix}$ termes.

On peut écrire une forme plus générale de la formule de Binet-Cauchy pour les mineurs d'une matrice.

Démonstration

On écrit A sous forme d'une liste de colonnes : A₁,..,A_n, et B en détaillant tous les coefficients. Le déterminant du produit AB est donc, en colonnes, de la forme

$\det(AB)=\det\left( \sum_{{j_1}=1}^n b_{{j_1}1} A_{j_1} ,\dots, \sum_{{j_m}=1}^n b_{{j_m}m} A_{j_m}\right)$

Il faut exploiter la multilinéarité du déterminant, et rassembler les termes correspondant au même det(A_S) en utilisant le caractère alterné. Le coefficient devant det(A_S) est identifié à det(B_S) en reconnaissant la formule de Leibniz.

Cette preuve peut être utilisée pour établir la propriété de produit des déterminants (une version plus géométrique a été établie dans l'article déterminant).

Interprétation euclidienne

Si A est une matrice réelle de taille m par n, alors le déterminant de la matrice A ^tA est égal au carré du volume m-dimensionnel du parallélotope engendré dans $\mathbb{R}^n$ par les m colonnes de A.

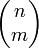La formule de Binet-Cauchy montre que cette quantité est égale à la somme des carrés des volumes des projections orthogonales sur les différents sous-espaces de coordonnées de dimension m (qui sont au nombre de $\begin{pmatrix}n\\m\end{pmatrix}$ ).

Dans le cas m=1, ces projections orthogonales sont des segments, et on retrouve une forme du théorème de Pythagore.

Portail des mathématiques

Ce document provient de « Formule de Binet-Cauchy ».

Catégorie : Déterminant

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formule De Binet-Cauchy de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Formule de binet-cauchy — Pour les articles homonymes, voir Cauchy et Binet. En algèbre linéaire, la formule de Binet Cauchy généralise la propriété de multiplicativité du déterminant d un produit au cas de deux matrices rectangulaires. On peut l écrire pour des matrices… … Wikipédia en Français
Formule de Binet-Cauchy — Pour les articles homonymes, voir Cauchy et Binet. En algèbre linéaire, la formule de Binet Cauchy généralise la propriété de multiplicativité du déterminant d un produit au cas de deux matrices rectangulaires. On peut l écrire pour des matrices… … Wikipédia en Français
Formule intégrale de Cauchy — Pour les articles homonymes, voir Cauchy. La formule intégrale de Cauchy est un point essentiel de l analyse complexe. Elle exprime le fait que la valeur en un point d une fonction holomorphe est complètement déterminée par les valeurs qu elle… … Wikipédia en Français
Identité de Binet-Cauchy — En mathématiques, et plus particulièrement en algèbre, l’identité de Binet–Cauchy, due à Jacques Philippe Marie Binet et Augustin Louis Cauchy, dit que[1] : pour des ensembles quelconques de nombres réels ou complexes (ou … Wikipédia en Français
Cauchy — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Cette page d’homonymie répertorie des personnes (réelles ou fictives) partageant un même patronyme. Patronyme Augustin Louis Cauchy (1789 1857),… … Wikipédia en Français
Binet — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Binet est un nom de famille notamment porté par : (par ordre alphabétique du prénom) Binet : maison de champagne ; Adolphe Gustave Binet… … Wikipédia en Français
Augustin-Louis Cauchy — Pour les articles homonymes, voir Cauchy. Augustin Louis Cauchy … Wikipédia en Français
Augustin Cauchy — Augustin Louis Cauchy Pour les articles homonymes, voir Cauchy. Augustin Louis Cauchy … Wikipédia en Français
Augustin Louis Cauchy — Pour les articles homonymes, voir Cauchy. Augustin Louis Cauchy Cauchy vers 1840. Lithographie de Zéphirin Belliard d après une peinture de Jean Roller … Wikipédia en Français
Produit de Cauchy — Pour les articles homonymes, voir Cauchy. En analyse, le produit de Cauchy est une opération portant sur certaines séries. Il permet de généraliser la propriété de distributivité. Son nom est un hommage à l analyste français Augustin Louis Cauchy … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Formule De Binet-Cauchy