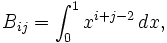Matrice de hilbert
- Matrice de hilbert
-
Matrice de Hilbert
En algèbre linéaire, la matrice de Hilbert est une matrice carrée de terme général Bij = 1 / (i + j − 1). Elle est nommée ainsi en hommage au mathématicien David Hilbert. Les matrices de Hilbert servent d'exemples classiques de matrices mal conditionnées, ce qui en rend l'usage très délicat en analyse numérique. Par exemple, le coefficient de conditionnement (pour la norme 2) de la matrice qui suit est de l'ordre de 4.8 · 105.
Ainsi la matrice de Hilbert de taille 5 vaut
![\mathcal{B} = \begin{pmatrix}
1 & \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} \\[4pt]
\frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} \\[4pt]
\frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7} \\[4pt]
\frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8} \\[4pt]
\frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8} & \frac{1}{9} \end{pmatrix}.](/pictures/frwiki/55/7ab716291db9abc1c05236f6fb8c428e.png)
Le déterminant de cette matrice peut être calculé de façon explicite, comme cas particulier d'un déterminant de Cauchy.
Si on interprète le terme général de la matrice de Hilbert comme
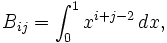
on peut y reconnaître une matrice de Gram pour les fonctions puissances et le produit scalaire adapté.
Les matrices de Hilbert sont définies positives.
Voir aussi
|
Articles en rapport avec les matrices |
| Par forme |
|
| Transformée |
|
| En relation |
|
| Par propriété |
|
| Par famille |
|
| Particulière |
|
| Associée |
|
| Résultats |
|
| Voir aussi |
|
 Portail des mathématiques
Portail des mathématiques
Catégorie : Matrice remarquable
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Matrice de hilbert de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Matrice De Hilbert — En algèbre linéaire, la matrice de Hilbert est une matrice carrée de terme général Bij = 1 / (i + j − 1). Elle est nommée ainsi en hommage au mathématicien David Hilbert. Les matrices de Hilbert servent d exemples classiques de matrices mal… … Wikipédia en Français
Matrice de Hilbert — En algèbre linéaire, la matrice de Hilbert est une matrice carrée de terme général Bij = 1 / (i + j − 1). Elle est nommée ainsi en hommage au mathématicien David Hilbert. Les matrices de Hilbert servent d exemples classiques de matrices mal… … Wikipédia en Français
Matrice Définie Positive — En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif. On introduit tout d abord les notations suivantes ; si a est une matrice à éléments réels ou complexes : aT désigne la… … Wikipédia en Français
Matrice definie positive — Matrice définie positive En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif. On introduit tout d abord les notations suivantes ; si a est une matrice à éléments réels ou… … Wikipédia en Français
Matrice définie positive — En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif : une matrice définie positive est une matrice positive inversible (la réciproque est fausse). On introduit tout d abord les… … Wikipédia en Français
Hilbert — David Hilbert David Hilbert David Hilbert en 1912 Naissance 23 janvier 1862 Königsberg (Prusse Orientale) … Wikipédia en Français
HILBERT (PROBLÈMES DE) — «Qui ne se réjouirait de pouvoir soulever le voile qui cache le futur, de jeter un regard sur le développement des mathématiques, ses progrès ultérieurs, les secrets des découvertes des siècles à venir?...» Prévoir le futur des mathématiques: qui … Encyclopédie Universelle
Matrice Semi-Définie Positive — En algèbre linéaire, la notion de matrice semi définie positive (on dit aussi : matrice positive) est analogue à celle de nombre réel positif ou nul. La notion de matrice semi définie positive est très proche de celle de matrice définie… … Wikipédia en Français
Matrice semi-definie positive — Matrice semi définie positive En algèbre linéaire, la notion de matrice semi définie positive (on dit aussi : matrice positive) est analogue à celle de nombre réel positif ou nul. La notion de matrice semi définie positive est très proche de … Wikipédia en Français
Matrice semi-définie positive — En algèbre linéaire, la notion de matrice semi définie positive (on dit aussi : matrice positive) est analogue à celle de nombre réel positif ou nul. La notion de matrice semi définie positive est très proche de celle de matrice définie… … Wikipédia en Français

![\mathcal{B} = \begin{pmatrix}
1 & \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} \\[4pt]
\frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} \\[4pt]
\frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7} \\[4pt]
\frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8} \\[4pt]
\frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8} & \frac{1}{9} \end{pmatrix}.](/pictures/frwiki/55/7ab716291db9abc1c05236f6fb8c428e.png)