Grand Icosidodécaèdre Tronqué
- Grand Icosidodécaèdre Tronqué
-
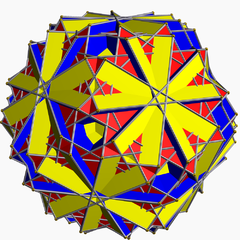
Grand icosidodécaèdre tronqué
En géométrie, le grand icosidodécaèdre tronqué est un polyèdre uniforme non-convexe, indexé sous le nom U68.
Coordonnées cartésiennes
Les coordonnées cartésiennes pour les sommets d'un grand icosidodécaèdre tronqué centré à l'origine sont toutes les permutations paires de
- (±τ, ±τ, ±(3−1/τ)),
- (±2τ, ±1/τ, ±(1−2/τ)),
- (±τ, ±1/τ2, ±(1+3/τ)),
- (±(1+2/τ), ±2, ±(2−1/τ)) and
- (±1/τ, ±3, ±2/τ),
où τ = (1+√5)/2 est le nombre d'or (quelquefois écrit φ).
Voir aussi
Liste des polyèdres uniformes
Lien externe
 Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Grand Icosidodécaèdre Tronqué de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Grand icosidodecaedre tronque — Grand icosidodécaèdre tronqué Grand icosidodécaèdre tronqué Type Polyèdre uniforme Éléments F=62, A=180, S=120 (χ=2) Faces par cotés 30{4}+20{6}+12{10/ … Wikipédia en Français
Grand icosidodécaèdre tronqué — Type Polyèdre uniforme Éléments F=62, A=180, S=120 (χ=2) Faces par côtés 30{4}+20{6}+12{10/3} … Wikipédia en Français
Icosidodécaèdre Tronqué — Grand rhombicosidodécaèdre Type Solide d Archimède Faces Carrés, Hexagones et Décagones Éléments : · Faces · Arêtes · Sommets · Caractéristique 62 180 120 … Wikipédia en Français
Icosidodécaèdre tronqué — Grand rhombicosidodécaèdre Type Solide d Archimède Faces Carrés, Hexagones et Décagones É … Wikipédia en Français
Grand Cuboctaèdre Tronqué — Type Polyèdre uniforme Éléments F=26, A=72, S=48 (χ=2) Faces par cotés 12{4}+8{6}+6{8/3} … Wikipédia en Français
Grand Icosaèdre Tronqué — Type Polyèdre uniforme Éléments F=32, A=90, S=60 (χ=2) Faces par cotés 12{5/2}+20{6} … Wikipédia en Français
Grand cuboctaedre tronque — Grand cuboctaèdre tronqué Grand cuboctaèdre tronqué Type Polyèdre uniforme Éléments F=26, A=72, S=48 (χ=2) Faces par cotés 12{4}+8{6}+6{8/3} … Wikipédia en Français
Grand icosaedre tronque — Grand icosaèdre tronqué Grand icosaèdre tronqué Type Polyèdre uniforme Éléments F=32, A=90, S=60 (χ=2) Faces par cotés 12{5/2}+20{6} … Wikipédia en Français
Grand Dodécaèdre Tronqué — Type Polyèdre uniforme Éléments F=24, A=90, S=60 (χ= 6) Faces par cotés 12{5/2}+12{10} … Wikipédia en Français
Grand cuboctaèdre tronqué — Type Polyèdre uniforme Éléments F=26, A=72, S=48 (χ=2) Faces par côtés 12{4}+8{6}+6{8/3} Configuration … Wikipédia en Français