- Intégrande
-
Intégration (mathématiques) - Wikipédia Intégration (mathématiques)
Pour les articles homonymes, voir intégration.L'intégration est un concept fondamental en mathématiques, issu du calcul des aires et de l'analyse, et utilisé dans de nombreuses branches des mathématiques. L'intégration permet, entre autres, à partir d'une fonction ƒ, de donner une mesure de l'espace délimité par la représentation graphique de ƒ.
L'opération de mesure de grandeurs (longueur d'une courbe, aire, volume, flux...) et de probabilité étant souvent soumise à des calculs d'intégrales, l'intégration est un outil fondamental pour une majeure partie de la science[1]. C'est la raison pour laquelle l'intégration est souvent abordée dès l'enseignement secondaire.
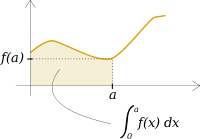
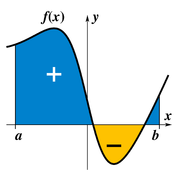
Définition du cas réel à partir de l'aire sous la courbe
Représentation graphique d'un intégrande ƒ positive et de son intégrale.
Représentation graphique d'un intégrande ƒ réelle et de son intégrale (avec signe)Si ƒ est une fonction réelle positive continue prenant ses valeurs dans un segment I = [0,a], alors l'intégrale de ƒ sur
Wikimedia Foundation. 2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Intégrande de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Fonction holomorphe — Une grille et son image par f une fonction holomorphe. Une fonction holomorphe est une transformation conforme. En analyse complexe, une fonction holomorphe est une fonction à valeurs dans , définie et dérivable en tout point d un sous ensemble… … Wikipédia en Français
Fonction Polylogarithme — La fonction polylogarithme (aussi connue sous le nom de fonction de Jonquière) est une fonction remarquable et peut être définie pour tout s et |z|<1 par : Le paramètre s et l argument z sont pris sur l ensemble , l ensemble des nombres… … Wikipédia en Français
Fonction polylogarithme — Les polylogarithmes ne doivent pas être confondus avec les fonctions polylogarithmiques, ni avec l écart du logarithme intégral qui possède une notation similaire. La fonction polylogarithme (aussi connue sous le nom de fonction de… … Wikipédia en Français
Polylogarithme — Fonction polylogarithme La fonction polylogarithme (aussi connue sous le nom de fonction de Jonquière) est une fonction remarquable et peut être définie pour tout s et |z|<1 par : Le paramètre s et l argument z sont pris sur l ensemble ,… … Wikipédia en Français
Critère de Nagumo — Dans le cadre des équations différentielles, le critère de Nagumo est un critère plus faible que le théorème de Cauchy Lipschitz donnant, tout comme le théorème de Cauchy Lipschitz, une condition suffisante pour garantir l existence et l unicité… … Wikipédia en Français
Développement de Laurent — Série de Laurent Karl Weierstrass. Cet article traite du développement en série de Laurent en analyse complexe. Pour la définition et les propriétés des séries de Laurent formelles en algèbre, veuillez consulter l article Série de Laurent… … Wikipédia en Français
Intégration (mathématiques) — Pour les articles homonymes, voir intégration. interprétée comme l’aire sous la courbe de f … Wikipédia en Français
Serie de Laurent — Série de Laurent Karl Weierstrass. Cet article traite du développement en série de Laurent en analyse complexe. Pour la définition et les propriétés des séries de Laurent formelles en algèbre, veuillez consulter l article Série de Laurent… … Wikipédia en Français
Série de Laurent — Une fonction holomorphe dans une couronne de centre c s y développe en série de Laurent ; les coefficients de la série s expriment comme des intégrales sur un chemin fermé γ contenu dans la couronne et entourant c. Cet article traite du… … Wikipédia en Français
Série de laurent — Karl Weierstrass. Cet article traite du développement en série de Laurent en analyse complexe. Pour la définition et les propriétés des séries de Laurent formelles en algèbre, veuillez consulter l article Série de Laurent formelle. En analyse… … Wikipédia en Français
- Contactez-nous: Support technique, RÉCLAME
