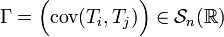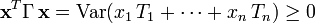Matrice semi-definie positive

Matrice semi-definie positive

Matrice semi-définie positive

En algèbre linéaire, la notion de matrice semi-définie positive (on dit aussi : matrice positive) est analogue à celle de nombre réel positif ou nul.

La notion de matrice semi-définie positive est très proche de celle de matrice définie positive.

Sommaire

Matrice symétrique réelle semi-définie positive

Soit M une matrice symétrique réelle d'ordre n. Elle est dite semi-définie positive si elle vérifie l'une des 2 propriétés équivalentes suivantes :

1. Pour toute matrice colonne 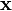\ \textbf{x} à n éléments réels, nous avons
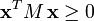\textbf{x}^{T} M\, \textbf{x} \geq 0.
2. Toutes les valeurs propres de M sont positives ou nulles, c'est-à-dire :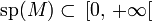
\ \mathrm{sp}(M) \subset\, [0,\, +\infty[\,.

Exemple

Étant donné un vecteur aléatoire 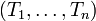(T_1,\dots, T_n) à valeurs dans \mathbb{R}^n dont chaque composante admet une variance, on définit sa matrice des covariances :

\Gamma = \Big(\mathrm{cov}(T_i, T_j) \Big) \in \mathcal{S}_n(\mathbb{R})
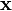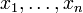  • Celle-ci est semi-définie positive. En effet, pour toute matrice colonne \ \textbf{x} à n éléments réels notés x_1,\dots, x_n :
\textbf{x}^{T} \Gamma\, \textbf{x} = \mathrm{Var}(x_1\, T_1 +\cdots + x_n\, T_n) \geq 0
  • Elle est définie positive si et seulement si la seule combinaison linéaire de 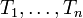T_1,\dots, T_n qui soit certaine est celle dont tous les coefficients sont nuls.

Matrice hermitienne semi-définie positive

On étend les propriétés et définitions précédentes aux matrices complexes hermitiennes.

Soit M une matrice hermitienne d'ordre n. Elle est dite semi-définie positive si elle vérifie l'une des 2 propriétés équivalentes suivantes :

1. Pour toute matrice colonne \ \textbf{z} à n éléments complexes, on a
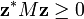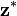\textbf{z}^{*} M \textbf{z} \geq 0 (où \textbf{z}^{*} désigne la matrice transconjuguée de \ \textbf{z}).
2. Toutes les valeurs propres de M sont positives ou nulles, c'est-à-dire :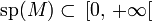
\ \mathrm{sp}(M) \subset\, [0,\, +\infty[\,.

Voir aussi

Matrice définie positive

Articles de mathématiques en rapport avec l'algèbre bilinéaire
modifier
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Matrice semi-d%C3%A9finie positive ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice semi-definie positive de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Matrice Semi-Définie Positive — En algèbre linéaire, la notion de matrice semi définie positive (on dit aussi : matrice positive) est analogue à celle de nombre réel positif ou nul. La notion de matrice semi définie positive est très proche de celle de matrice définie… …   Wikipédia en Français

  • Matrice semi-définie positive — En algèbre linéaire, la notion de matrice semi définie positive (on dit aussi : matrice positive) est analogue à celle de nombre réel positif ou nul. La notion de matrice semi définie positive est très proche de celle de matrice définie… …   Wikipédia en Français

  • Matrice Définie Positive — En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif. On introduit tout d abord les notations suivantes ; si a est une matrice à éléments réels ou complexes : aT désigne la… …   Wikipédia en Français

  • Matrice definie positive — Matrice définie positive En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif. On introduit tout d abord les notations suivantes ; si a est une matrice à éléments réels ou… …   Wikipédia en Français

  • Matrice semi-simple — En algèbre linéaire, la notion de matrice semi simple constitue une généralisation de la notion de matrice diagonalisable. Elle permet de discriminer deux types d obstruction à la diagonalisabilité : d une part les obstructions liées à l… …   Wikipédia en Français

  • Matrice hermitienne — Hermitien Plusieurs entités mathématiques sont qualifiées d hermitiennes en référence au mathématicien Charles Hermite. Sommaire 1 Espace hermitien 2 Produit scalaire hermitien 3 Opérateur hermitien …   Wikipédia en Français

  • Matrice hermitique — Hermitien Plusieurs entités mathématiques sont qualifiées d hermitiennes en référence au mathématicien Charles Hermite. Sommaire 1 Espace hermitien 2 Produit scalaire hermitien 3 Opérateur hermitien …   Wikipédia en Français

  • Matrice de Gram — Déterminant de Gram En géométrie euclidienne ou hilbertienne, le déterminant de Gram permet de calculer des volumes et de tester l indépendance linéaire d une famille de vecteurs. Il associe des calculs de produits scalaires et d un déterminant.… …   Wikipédia en Français

  • Matrice Laplacienne — En théorie des graphes, une matrice laplacienne, ou matrice de Laplace, est une matrice représentant un graphe. Définition La matrice laplacienne d un graphe G non orienté et non réflexif est définie par : Ml = Md − Ma où Md est la matrice… …   Wikipédia en Français

  • Matrice positive — Sommaire 1 Matrice positive 1.1 Définitions 1.2 Relation d ordre sur les matrices réelles 2 Matrices carrées positives …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”