- Polyèdre adouci
-
En géométrie, un polyèdre adouci est un polyèdre obtenu en écartant les faces d'un polyèdre et en comblant les trous par des triangles équilatéraux. Souvent, cela consiste à remplacer chaque sommet du polyèdre par un triangle équilatéral et chaque arête par deux triangles équilatéraux.
L'appellation "adouci" vient du fait que le polyèdre obtenu par cette déformation possède des angles dièdres beaucoup moins aigus et une surface plus proche de celle de la sphère.
Sommaire
Chiralité et groupes de symétrie
La plupart des polyèdres adoucis sont chiraux.
Les polyèdre adoucis chiraux n'ont pas de symétries réflectives, ils ont de ce fait 2 formes énantiomorphes qui sont symétriques l'une de l'autre dans un miroir non supperposables. C'est le cas du cube adouci :


Ils ont cependant des groupes de symétrie qui sont des rotations qui laissent le polyèdre globalement inchangé. Il y en a deux grands types :
- O : La symétrie octaédrale, groupe du cube et de l'octaèdre, d'ordre 24.
- I : La symétrie icosaédrale, groupe du dodécaèdre et de l'icosaèdre, d'ordre 60.
Liste des polyèdres adoucis
Polyèdres adoucis uniformes
Il y a en tout 12 polyèdres adoucis uniformes.
Mais on rajoute ici également :
- L'icosaèdre régulier (qui est cependant rarement considéré comme tel), mais il peut être en effet obtenu en changeant les 4 sommets d'un tétraèdre par 4 triangles et ses 6 arêtes par 6 paires de triangles :
 , on obtient bien un icosaèdre.
, on obtient bien un icosaèdre. - Le grand dirhombidodécaèdre disadouci qui n'est pas considéré comme strictement uniforme (mais seulement uniforme au sens large), car il possède la particularité étrange de faire se rencontrer plus de deux faces sur une même arête. Il est parfois appelé "polyèdre de Skilling".
Les polyèdres adoucis uniformes Polyèdre adouci Image Polyèdre d'origine Image Groupe de symétrie icosaèdre 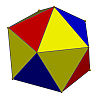
tétraèdre 
I + symétries réflectives cube adouci 
cube 
O dodécaèdre adouci 
dodécaèdre 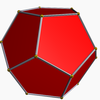
I grand dodécicosidodécaèdre adouci 
grand dodécicosidodécaèdre 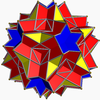
I icosidodécadodécaèdre adouci 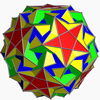
icosidodécadodécaèdre 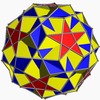
I dodécadodécaèdre adouci 
dodécadodécaèdre 
I dodécadodécaèdre adouci inversé 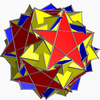
dodécadodécaèdre 
I grand icosidodécaèdre adouci inversé 
grand icosidodécaèdre 
I grand icosidodécaèdre rétroadouci 
grand icosidodécaèdre 
I grand icosidodécaèdre adouci 
grand icosidodécaèdre 
I petit icosicosidodécaèdre adouci 
petit icosicosidodécaèdre 
I + symétries réflectives petit icosicosidodécaèdre rétroadouci 
petit icosicosidodécaèdre 
I + symétries réflectives grand dirhombicosidodécaèdre 
I + symétries réflectives grand dirhombidodécaèdre disadouci 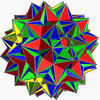
grand dirhombicosidodécaèdre 
I + symétries réflectives Quelques remarques :
- Les trois premiers sont les seuls à être convexes et non-croisés. Ils sont obtenus par l'adoucissement de solides de Platon, à savoir, respectivement : le tétraèdre, le cube et le dodécaèdre. Il est impossible d'adoucir les deux autres solides de Platon (à savoir l'icosaèdre et l'octaèdre) parce qu'on obtiendrait alors plus de 6 triangles équilatéraux à un même sommet : impossible (et également parce qu'il faudrait remplacer un sommet d'ordre 4 ou 5 par un triangle qui ne remplace que les sommets d'ordre 3).
- Le cube adouci est le seul à posséder un groupe de symétrie de type O.
- L'icosaèdre et les quatre derniers ont, en plus de leur groupe de rotations, des symétries réflectives.
Polyèdres adoucis non-uniformes
Deux des solides de Johnson sont également adoucis : le disphénoïde adouci et l'antiprisme carré adouci. Chacun des deux est formé par séparation du polyèdre d'origine en deux (le long d'arêtes) et par remplissage de l'écart par des triangles. Aucun n'est chiral.
Les polyèdres adoucis non-uniformes Polyèdre adouci Image Polyèdre d'origine Image Groupe de symétrie disphénoïde adouci 
disphénoïde 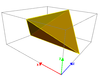
D2d antiprisme carré adouci 
antiprisme carré 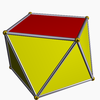
D4d Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Snub polyhedron » (voir la liste des auteurs)
Wikimedia Foundation. 2010.
