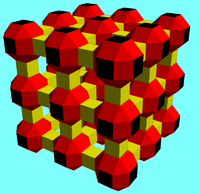
- Polyedre oblique infini
-
Polyèdre oblique infini
En géométrie, les polyèdres obliques infinis sont une définition étendue des polyèdres, créés par des faces polygonales régulières, et des figures de sommet non-planaires.
Beaucoup sont directement reliés aux nids d'abeille convexes uniformes, étant la surface polygonale d'un nid d'abeille avec certaines cellules enlevées. En tant que solides, ils sont appelés nids d'abeille partiels et aussi éponges.
Ces polyèdres sont aussi appelés pavages hyperboliques parce qu'ils peuvent être regardés comme reliés aux pavages de l'espace hyperbolique qui ont aussi un angle de déflexion négatif.
Sommaire
Polyèdres obliques réguliers
Selon Coxeter, en 1926 John Flinders Petrie a généralisé le concept de polygones obliques réguliers (polygones non-planaires) aux polyèdres obliques réguliers.
Il existe 3 polyèdres obliques réguliers :
- {4,6|4} : 6 carrés sur un sommet (relié au nid d'abeille cubique, construit avec des cellules cubiques, en enlevant deux faces opposées sur chacune et en reliant tous les ensembles de six autour d'un cube sans face).
- {6,4|4} : 4 hexagones sur un sommet (relié au nid d'abeille cubique bitronqué, construit avec des octaèdres tronqués avec leurs faces carrées enlevées et reliant les paires de trous ensemble).
- {6,6|3} : 6 hexagones sur un sommet (relié au nid d'abeille cubique quart, construit avec des cellules tétraèdrique tronquées, en enlevant les faces triangulaires, et en reliant les ensembles de quatre autour d'un tétraèdre sans face).
Leurs figures de sommet sont des polygones obliques, zig-zaggant entre deux plans.
Voici quelques représentations partielles, des vues verticales projetées de leurs figures de sommet obliques et des nids d'abeille uniformes correspondant partiellement.
{4,6|4}
{6,4|4}
{6,6|3}
4.4.4.4.4.4
6.6.6.6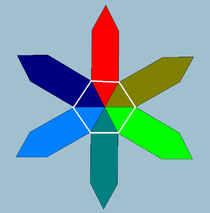
6.6.6.6.6.6
Nid d'abeille cubique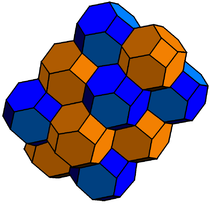
Cubique bitronqué
Cubique alterné bitronquéPolyèdres obliques réguliers prismatiques
Il existe aussi deux formes prismatiques régulières, disqualifiées par Coxeter (parmi d'autres) de l'appellation régulière parce qu'elles ont des faces coplanaires adjacentes.
- 5 carrés sur un sommet (deux pavages carrés parallèles connectés par des trous cubiques).
- 8 triangles sur un sommet (deux pavages triangulaires parallèles connectés par des trous octaèdriques).
Au-delà de l'espace tridimensionnel euclidien, C. W. L. Garner a déterminé un ensemble de 32 polyèdres obliques réguliers dans un espace tridimensionnel hyperbolique, dérivé des 4 nids d'abeilles hyperboliques réguliers.
Polyèdres obliques semi-réguliers
Il existe beaucoup d'autres polyèdres obliques semi-régulier (de sommet uniforme), découverts par A.F. Wells et J.R. Gott (il les ont appelés pseudopolyèdres) dans les années 60.
Un polyèdre oblique prismatique semi-régulier avec une configuration de sommet 4.4.4.6.Fichier:Skew polyhedron 4646.png
Un polyèdre oblique semi-régulier (partiel) avec une configuration de sommet 4.8.4.8. Relié au nid d'abeille cubique omnitronqué.
Un polyèdre oblique semi-régulier (partiel) avec une configuration de sommet 3.4.4.4.4. Relié au nid d'abeille cubique runcitronqué.Références
- Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0486409198 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
- Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
- Garner, C. W. L. Regular Skew Polyhedra in Hyperbolic Three-Space. Canad. J. Math. 19, 1179-1186, 1967.
Liens externes
- Weisstein, Eric W., Regular Skew Polyhedron at MathWorld.
- SkewOlshevsky, George, Skew polytope at Glossary for Hyperspace.
- "Hyperbolic" Tessellations
- Infinite Regular Polyhedra [1]
- Infinite Repeating Polyhedra - Partial Honeycombs in 3-Space
- 18 SYMMETRY OF POLYTOPES AND POLYHEDRA, Egon Schulte: 18.3 REGULAR SKEW POLYHEDRA
Portail de la géométrie
Catégorie : Polyèdre
Wikimedia Foundation. 2010.
