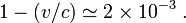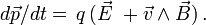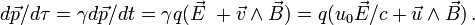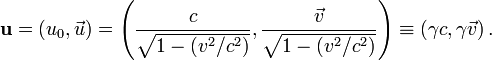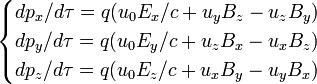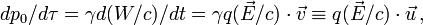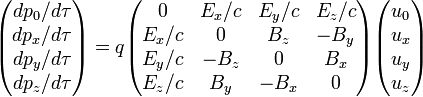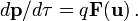- Relativite restreinte
-
Relativité restreinte
 Pour les articles homonymes, voir relativité.
Pour les articles homonymes, voir relativité.
Cet article de physique fait
partie de la série relativitéAvant Einstein Histoire de la physique Michelson - Lorentz Mach - Poincaré - Hilbert exp:Michelson et Morley - éther Avec Einstein Principe de relativité Principe d'équivalence c - transformation de Lorentz espace-temps - E=mc² - temps exp:pensée?-jumeaux-train relativité restreinte-générale controverse historique En physique des particules cyclotron accélérateur de particules Feynman - EQR Méta Formulaire de physique Tous les articles sur la relativité La relativité restreinte est la théorie formelle élaborée par Albert Einstein en 1905 en vue de tirer toutes les conséquences physiques de la relativité galiléenne et du principe que la vitesse de la lumière dans le vide a la même valeur dans tous les référentiels inertiels, ce qui était implicitement énoncé dans les équations de Maxwell (mais interprété bien différemment jusque-là avec « l'espace absolu » de Newton et l'éther).
La relativité galiléenne stipule, en langage moderne, que toute expérience faite dans un référentiel inertiel se déroulerait de manière parfaitement identique dans tout autre référentiel inertiel. Devenue « principe de relativité », son énoncé sera ensuite modifié par Einstein pour être étendu aux repères non-inertiels : de « restreinte » la relativité deviendra « générale ».
La théorie de la relativité restreinte a établi de nouvelles formules permettant de passer d'un référentiel galiléen à un autre. Les équations correspondantes conduisent à des phénomènes qui heurtent le sens commun (mais qui ont tous été confirmés expérimentalement), un des plus étonnants et des plus célèbres étant connu sous le nom de paradoxe des jumeaux (un paradoxe qui a été parfois utilisé en science-fiction[1]).
La relativité restreinte a eu également un impact en philosophie en éliminant toute possibilité d'existence d'un temps et de durées absolues dans l'ensemble de l'univers. À la suite de Henri Poincaré, elle a forcé les philosophes à se poser différemment la question du temps et de l'espace.
Origines de la théorie
Bref historique
En mécanique newtonienne, les vitesses s'ajoutent, c'est la relativité galiléenne : si d'une fusée se déplaçant à la vitesse de 7 km/s par rapport à la Terre on tire un boulet de canon vers l'avant à la vitesse de 1 km/s par rapport à la fusée, la vitesse du projectile par rapport à la Terre sera de 8 km/s. Si le boulet est tiré vers l'arrière, sa vitesse sera de 6 km/s.
À la fin du XIXe siècle, James Clerk Maxwell établit les équations régissant les ondes électromagnétiques et notamment les ondes lumineuses[2]. Selon cette théorie la vitesse de la lumière ne devait dépendre que des propriétés électriques et magnétiques du milieu, ce qui posait un problème dans le cas où ce milieu est le vide car cela suggère une indépendance de la vitesse de la lumière par rapport au référentiel de l'instrument de mesure : si on émet un faisceau lumineux depuis la fusée vers l'avant ou vers l'arrière la vitesse de la lumière mesurée par rapport à la Terre sera la même, contrairement au boulet. L'hypothèse de l'éther, milieu de propagation de la lumière, donc hypothèse assez naturelle, devait enlever à la lumière cette propriété et rendre sa propagation compatible avec la relativité galiléenne. En 1887, une expérience a été conduite par Michelson et Morley pour mesurer la vitesse de la terre par rapport à cet éther : expérience similaire à celle de la fusée évoquée ci-dessus, et où la Terre tient elle-même le rôle de la fusée. Ils voulaient mesurer cette vitesse en mettant en évidence la différence de vitesse de la lumière entre différentes directions de propagation possibles. N'ayant pas détecté une différence significative, le résultat de cette expérience s'avéra difficile à interpréter, tant et si bien que leurs auteurs allèrent jusqu'à imaginer une contraction, inexpliquée, des instruments de mesure dans certaines directions : la relativité restreinte justifira cela par la suite.
Des formules de transformation pour passer d'un observateur à un autre furent établies par Lorentz avant 1904[réf. nécessaire]; il s'agissait d'équations de compatibilité dont la signification n'était pas claire aux yeux de leur auteur. D'autres physiciens avaient eu une démarche similaire plus tôt encore. Poincaré a publié des articles pour en trouver une interprétation, peu de temps avant Einstein[3]. La répartition des rôles de tel ou tel savant dans l'émergence de la théorie de la relativité restreinte a fait l'objet d'une controverse, en particulier dans les années 2000.
En 1905, dans son article intitulé De l'électrodynamique des corps en mouvement[4], Albert Einstein présenta la relativité comme suit :
- L'éther est une notion arbitraire qui n'est pas utile à l'expression de la théorie de la relativité.
- La célérité de la lumière par rapport aux observateurs ne dépend pas de leur vitesse.
- Les lois de la physique respectent le principe de relativité.
Les équations de Lorentz qui en découlent sont conformes à la réalité physique. Elles ont des conséquences inattendues. Ainsi un observateur attribue à un corps en mouvement une longueur plus courte que la longueur attribuée à ce même corps au repos et la durée des phénomènes qui affectent le corps en mouvement est allongée par rapport à cette « même » durée mesurée par des observateurs immobiles par rapport à ce corps.
Einstein a également réécrit les formules qui définissent la quantité de mouvement et l'énergie cinétique de manière à les rendre invariantes dans une transformation de Lorentz.
Le temps et les trois coordonnées d'espace jouant des rôles indissociables dans les équations de Lorentz, Minkowski les interpréta dans un espace-temps à quatre dimensions. Remarquons toutefois que le temps et l'espace restent de natures différentes et qu'on ne peut donc pas assimiler l'un à l'autre. Par exemple on peut faire demi-tour dans l'espace alors que cela est impossible dans le temps.
Attitude du comité Nobel
En 1912, Lorentz et Einstein furent proposés pour un prix Nobel conjoint pour leur travail sur la théorie. La recommandation était de Wien, lauréat de 1911, qui déclare que « bien que Lorentz doit être considéré comme le premier à avoir trouvé le contenu mathématique du principe de relativité, Einstein réussit à le réduire en un principe simple. On devrait dès lors considérer le mérite des deux chercheurs comme comparable ». Einstein ne reçut jamais le Nobel pour la relativité, le prix Nobel n'étant, en principe, jamais accordé pour une théorie pure. Le comité attendit donc une confirmation expérimentale. Le temps que cette dernière se présente, Einstein était passé à d'autres travaux importants[5].
Einstein se verra finalement décerner le prix Nobel de physique en 1921[6], pour ses apports à la physique théorique[7], et tout spécialement pour son explication de l'effet photoélectrique.
La théorie
Les postulats d'Einstein (1905)
La théorie d'Einstein est centrée sur le principe de relativité qui concerne l'observation et la mesure des phénomènes en fonction du référentiel depuis lequel l'observateur (ou l'appareil de mesure) effectue les mesures sur l'expérience.
La relativité resteinte ne considère que le cas où l'observateur est dans un référentiel inertiel, les autres référentiels sont l'objet d'étude de la relativité générale. Rappelons qu'un référentiel est dit inertiel si tout objet isolé (sur lequel ne s’exerce aucune force ou sur lequel la résultante des forces est nulle) est soit immobile, soit en mouvement de translation rectiligne uniforme. Par exemple : une fusée dans l'espace loin de toute masse constitue un repère inertiel si aucun moteur n'est allumé.
Les postulats de la relativité restreinte sont les suivants :
- Les lois de la physique ont la même forme dans tous les référentiels inertiels
- La vitesse de la lumière dans le vide a la même valeur dans tous les référentiels inertiels
Le premier postulat est le principe de relativité proprement dit, dans sa conception restreinte à la classe des référentiels inertiels. Il formalise un constat de Galilée selon lequel le mouvement rectiligne uniforme est « comme rien » pour l'observateur appartenant au référentiel mobile.
Le second postulat formalise l'interprétation des équations de Maxwell suivant laquelle il n'y a pas d'éther, et est conforme aux expériences. Une des conséquences est que la vitesse de la lumière est indépassable, ce qui oblige à synchroniser les horloges d'un référentiel donné par utilisation de signaux lumineux : il suffit que le « gardien du temps » émette un top horaire, disons à midi. Puis, lorsque l'observateur situé à la distance r recevra le top il tiendra compte du temps r /c que le top aura mis à lui parvenir et mettra son horloge à l'heure « midi+r /c ».
On peut se passer du second postulat pour déterminer les équations des transformations de Lorentz à condition d'introduire une hypothèse supplémentaire au premier postulat : l'espace-temps est homogène et isotrope. Ce fait a été découvert dès 1910 par Kunz[8] et indépendamment par Comstock[9]. L'hypothèse additionnelle conduit à un groupe de transformations, dépendant d'un paramètre c2, physiquement homogène au carré d'une vitesse. Ces transformations s'identifient aux transformations de Galilée si c2 est infini et aux transformations de Lorentz si c2 est fini positif[10]. L'identification de c à la vitesse de la lumière, établie comme finie par les observations, se traduit par le second postulat. Jean-Marc Levy-Leblond fait remarquer que cette approche implique seulement l'existence d'une vitesse-limite c, qui est celle de toutes les particules sans masse, et donc de la lumière dans nos théories actuelles. Si le photon devait s'avérer avoir une masse (voir à ce sujet les propriétés physiques du photon), la relativité ne serait pas remise en question, mais la lumière aurait une vitesse légèrement inférieure à c, et qui dépendrait des référentiels[11].
Synchronisation des horloges
Article détaillé : Synchronisation d'horloge.Plaçons nous dans une situation idéale où les difficultés techniques sont surmontées sans même y penser.
Dans le référentiel d'un observateur, étant donné une horloge immobile utilisée comme référence, il faut synchroniser une autre horloge du référentiel (c'est-à-dire une horloge immobile dans ce référentiel). Pour cela, il faut déterminer la distance entre les deux : une unité de mesure des longueurs étant connue, et sachant que la vitesse de la lumière (connue aussi, et indépassable) ne dépend pas du référentiel, il suffit de déterminer le temps mis par la lumière pour faire l'aller-retour entre les deux horloges ; mais une méthode plus manuelle peut tout aussi bien faire l'affaire. Ensuite, pour régler les deux horloges de telle sorte qu'elles aient la même unité de mesure du temps et le même temps zéro, il suffit qu'elles communiquent à la vitesse de la lumière, et, pour l'initialisation du temps zéro, que l'on tienne compte du temps mis par l'information pour aller de l'une à l'autre.Ainsi, si un événement a lieu loin de l'horloge de référence, il peut être précisément localisé et daté par une horloge proche et immobile (dans le référentiel).
Mesure du temps et des longueurs dans les référentiels
Deux référentiels inertiels étant donnés, en translation rectiligne uniforme l'un par rapport à l'autre, comment s'assurer qu'ils ont le même système de mesure du temps et des longueurs ?[12]
- Tout d'abord, dans un seul référentiel, les hypothèses de l'isotropie et de l'homogénéité de l'espace impliquent que les mesures que l'on peut faire sur un objet ne dépendent pas de sa position dans le référentiel.
- En transmettant des doubles de l'unité de mesure et de l'horloge de référence d'un référentiel inertiel à l'autre, on leur fait subir une accélération (pour passer de l'immobilité dans l'un à l'immobilité dans l'autre), ce qui implique que ces doubles ne sont pas dans un référentiel inertiel durant cette phase mais dans un référentiel accéléré : on peut imaginer que dans ce référentiel transitoire, leurs propriétés ne sont plus les mêmes. Mais une fois l'immobilité acquise dans le nouveau référentiel, le principe de relativité implique qu'ils ont les mêmes propriétés que dans leur précédent référentiel inertiel : les unités de mesures sont les mêmes dans les deux référentiels. Ce sera la vitesse relative entre les deux référentiels qui va donner des différences de mesures pour une même expérience.
Les transformations de Lorentz
Article détaillé : Transformations de Lorentz.On considère deux référentiels
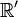 et
et  , le premier référentiel
, le premier référentiel 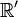 étant animé de la vitesse
étant animé de la vitesse  par rapport au référentiel
par rapport au référentiel  . Pour simplifier le calcul on travaille d'abord dans le cadre de transformations dites « spéciales », caractérisées par le fait que les systèmes d'axes x, y, z et x', y', z' sont parallèles, que les axes O ’x ’ et Ox sont communs et parallèles à la vitesse
. Pour simplifier le calcul on travaille d'abord dans le cadre de transformations dites « spéciales », caractérisées par le fait que les systèmes d'axes x, y, z et x', y', z' sont parallèles, que les axes O ’x ’ et Ox sont communs et parallèles à la vitesse  , et en supposant que quand les origines spatiales des deux référentiels étaient confondues, les horloges (fixes dans les référentiels respectifs, en O et O') indiquaient toutes deux t = 0 et t' = 0 (initialisation des horloges). Cette restriction ne nuit nullement à la généralité des résultats. On écrira ci-dessous les formules relatives à une vitesse pointant dans une direction quelconque.
, et en supposant que quand les origines spatiales des deux référentiels étaient confondues, les horloges (fixes dans les référentiels respectifs, en O et O') indiquaient toutes deux t = 0 et t' = 0 (initialisation des horloges). Cette restriction ne nuit nullement à la généralité des résultats. On écrira ci-dessous les formules relatives à une vitesse pointant dans une direction quelconque.Les hypothèses d'Einstein conduisent aux transformations dites « de Lorentz ». Les formules de Lorentz permettent d'exprimer les coordonnées (x, y, z, t) d'un événement donné dans le repère « fixe » (disons la Terre) en fonction des coordonnées (x ’, y ’, z ’, t ’ ) du même événement dans le repère « mobile » (disons une fusée). Elles s'écrivent :
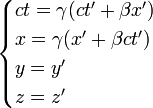
où β et γ sont des facteurs sans dimension définis par
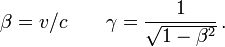
Ces expressions se simplifient et prennent une forme proche d'une rotation si on fait intervenir les fonctions hyperboliques de paramètre θ, appelé rapidité, qui est un angle de « rotation » dans l'espace de Minkowski, défini par

Avec ces notations on obtient
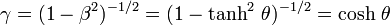 et
et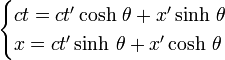
Pour obtenir les formules correspondant à la transformation inverse il suffit de changer β en -β, et donc θ en -θ.
Une recette : pour trouver le signe à mettre devant sinh θ il suffit de considérer un point au repos dans l'un des repères (disons celui de la fusée, avec x ’ = 0 par exemple) et de voir quel doit être le signe de la coordonnée spatiale dans l'autre repère (disons le repère fixe dans lequel x croît si la fusée a une vitesse positive).
Transformations de Lorentz pour une direction arbitraire de la vitesseSi les transformations spéciales simplifient l'étude analytique, elles ne nuisent en rien à la généralité. On peut aisément passer au cas où les référentiels en mouvement ne sont pas parallèles l'un à l'autre, et sont d'orientation quelconque par rapport à leur vitesse relative
 . Il est toujours possible de décomposer le vecteur
. Il est toujours possible de décomposer le vecteur  suivant deux directions : celle parallèle au déplacement
suivant deux directions : celle parallèle au déplacement  et celle orthogonale à celle-ci
et celle orthogonale à celle-ci 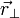 . On a donc :
. On a donc : 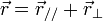
En posant
les transformations de Lorentz donnent :
ce qui conduit à
Comme
on a (en multipliant vectoriellement par
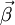 )
)On obtient donc l'expression des transformations générales de Lorentz sous la forme :
Dilatation du temps et contraction des longueurs
Les transformations de Lorentz mènent à une vision révolutionnaire de la physique et font apparaître des phénomènes qui heurtent le sens commun.
Dans les exemples qui suivent nous allons être amenés à considérer deux événements successifs. On réécrira donc les formules précédentes en remplaçant les x et les t par des Δx et des Δt représentant l'écart spatial ou temporel entre le premier événement et le second.
Dilatation des durées
Article détaillé : Dilatation du temps.L'intervalle de temps séparant deux événements dans un référentiel est mesuré par une quantité différente dans un autre référentiel.
Considérons le référentiel terrestre constitué par un ensemble d'observateurs au repos les uns par rapport aux autres et munis d'horloges synchronisées. Ces observateurs terrestres sont situés le long du trajet d'une fusée se déplaçant à la vitesse v par rapport au repère de la Terre. Supposons que la fusée émette un éclair toutes les secondes, le déclenchement du signal étant commandé par une horloge interne à la fusée. Dans la fusée la période de temps entre deux flashs est donc égale à 1 seconde et sera notée Δt'. Les flashs successifs étant émis au même point pour la fusée, l'intervalle spatial Δx' qui les sépare dans ce repère est nul. Comment la période de ces éclairs va-t-elle être perçue par les observateurs terrestres disposés le long du parcours de la fusée ?
Puisque Δx' = 0 l'équation de Lorentz
montre que l'intervalle Δt entre les éclairs successifs perçus par les observateurs liés au repère terrestre (et dont les horloges, rappelons-le, marquent toutes la même heure) est donné par
Cette expression indique que Δt est toujours plus grand que Δt '. Ainsi, l'intervalle de temps entre deux éclairs mesuré par 1 seconde dans le référentiel de la fusée est mesuré par γ secondes (γ > 1) dans le référentiel terrestre. On peut dire encore que les observateurs terrestres voyant l'horloge de la fusée à travers le hublot constatent que cette horloge retarde (les horloges terrestres doivent tourner γ secondes, donc plus d'une seconde, avant de voir l'horloge de la fusée tourner d'une seconde)[13]. Pour dire les choses rapidement, une horloge embarquée paraît ralentir. C'est cet effet qu'on appelle la dilatation relativiste du temps. Il est à l'origine du paradoxe des jumeaux, le jumeau revenant d'un voyage imaginaire à une vitesse proche de celle de la lumière (ce qui est évidemment technologiquement impossible à réaliser pour le moment)[14] se retrouvant au retour plus jeune que son frère resté sur Terre, puisque son horloge de voyageur aura moins tourné que celle du sédentaire.
Considérons le cas où deux événements sont tels qu'ils se produisent en un même point de l'espace dans un certain référentiel. D'après la formule ci-dessus c'est dans ce référentiel que, lue sur une seule et même horloge, la durée mesurée est la plus courte. On lui attribue le nom de durée propre. Pour tout référentiel par rapport auquel le voyageur se déplace, la durée entre les deux mêmes événements demande, pour sa mesure, deux horloges, une en chacun des points du référentiel où se trouvera le voyageur à l'instant initial et à l'instant final. Cette durée sera toujours plus longue que la durée propre.
Les vérifications expérimentales sont nombreuses : durée de vie de muons atmosphériques, durée de vie de particules dans les accélérateurs, marche des horloges embarquées des satellites (le phénomène sert dans ce cas à isoler l'effet de la gravitation), etc.
Contraction des longueurs
Article détaillé : contraction des longueurs.Supposons que dans le référentiel
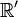 de la fusée se trouve une règle fixe, de longueur L', le long de l'axe O'x'. Cette longueur mesurée dans le référentiel dans lequel la règle est fixe est la longueur propre de la règle.
de la fusée se trouve une règle fixe, de longueur L', le long de l'axe O'x'. Cette longueur mesurée dans le référentiel dans lequel la règle est fixe est la longueur propre de la règle.Dans le référentiel
 de la Terre, par rapport auquel la règle se meut, on pourra mesurer la longueur de la règle en considérant les deux événements suivants : le premier sera défini comme celui du passage de la première extrémité de la règle en face de tel observateur terrestre lorsque son horloge indiquera (disons) midi, le second sera celui du passage de la seconde extrémité de la règle en face d'un autre observateur terrestre à la même heure, toujours midi. La distance des deux observateurs sera considérée comme une mesure de la longueur de la règle dans le repère fixe puisqu'elle représente la distance entre les points de
de la Terre, par rapport auquel la règle se meut, on pourra mesurer la longueur de la règle en considérant les deux événements suivants : le premier sera défini comme celui du passage de la première extrémité de la règle en face de tel observateur terrestre lorsque son horloge indiquera (disons) midi, le second sera celui du passage de la seconde extrémité de la règle en face d'un autre observateur terrestre à la même heure, toujours midi. La distance des deux observateurs sera considérée comme une mesure de la longueur de la règle dans le repère fixe puisqu'elle représente la distance entre les points de  qui coïncident avec les extrémités de la règle au même instant de
qui coïncident avec les extrémités de la règle au même instant de  . Comme Δt = 0, l'équation de Lorentz
. Comme Δt = 0, l'équation de Lorentzs'écrit
Par conséquent, la longueur L mesurée sur Terre est
de sorte que L est plus petit que L’.
Il faut cependant se défendre d'appliquer ce phénomène de contraction des longueurs de façon irréfléchie. Il faut toujours passer par la définition soigneuse des événements en cause et examiner comment leurs coordonnées changent d'un repère à l'autre. Autrement on peut tomber sur de nombreux paradoxes[15]. L'un des plus connus relatifs à cette contraction relativiste des longueurs est celui de la voiture censée rentrer dans un garage plus court qu'elle, à condition de rouler assez vite.
-
- voir aussi : Paradoxe du train
Relativité de la simultanéité
Article détaillé : Simultanéité.La modification de la valeur des durées entre deux événements lors du passage d'un référentiel à l'autre a souvent été exploitée dans les premières présentations de la théorie de la relativité, notamment par Einstein. En particulier la relativité limite la notion de simultanéité aux événements vus à partir d'un seul référentiel galiléen.
Deux événements simultanés dans
 , en deux points différents de
, en deux points différents de  , ne sont plus simultanés dans un autre référentiel en mouvement par rapport à
, ne sont plus simultanés dans un autre référentiel en mouvement par rapport à  . Puisque l'intervalle spatio-temporel au sens de la relativité restreinte entre deux événements est indépendant du repère choisi, on voit que l'intervalle entre deux événements simultanés dans un certain repère est nécessairement du type espace, ce qui signifie que le terme c2Δt2 − Δx2 est négatif. Autrement dit de tels événements sont ailleurs l'un de l'autre, c'est-à-dire qu'ils ne peuvent pas être associés par un lien de cause à effet.
. Puisque l'intervalle spatio-temporel au sens de la relativité restreinte entre deux événements est indépendant du repère choisi, on voit que l'intervalle entre deux événements simultanés dans un certain repère est nécessairement du type espace, ce qui signifie que le terme c2Δt2 − Δx2 est négatif. Autrement dit de tels événements sont ailleurs l'un de l'autre, c'est-à-dire qu'ils ne peuvent pas être associés par un lien de cause à effet.Illustration simple
Dans l'expérience suivante, qui illustre de façon simple la dilatation du temps prévue par la relativité restreinte, on considère une montre à photons dans laquelle un grain de lumière effectue à la vitesse c de la lumière des allers-retours entre deux miroirs.
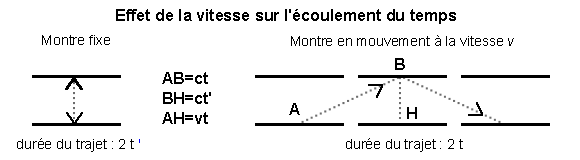
La durée d'un aller-retour dans un repère est égale au quotient du trajet effectué dans ce repère par la célérité de la lumière, laquelle ne dépend pas du repère. Si la montre est fixe par rapport à l'observateur, le trajet correspond à la distance au repos entre les deux miroirs et dure un temps 2t '. Si la montre se déplace par rapport à l'observateur, celui-ci verra le photon suivre une ligne brisée plus longue que le segment parcouru dans le repère précédent. La durée 2t du parcours est supérieure à 2t ' : la montre en mouvement retarde (il y a dilatation du temps).
La longueur de l'hypoténuse du triangle rectangle ABH de la figure est ct, celle de la hauteur est ct ' et celle de la base est vt si on note v la vitesse de translation de la montre dans le repère « fixe ». On a donc (théorème de Pythagore) :
d'où on tire immédiatement
On retrouve donc de façon simple la formule antérieure donnant la dilatation du temps.
La célérité de la lumière étant de 300 000 km/s, un avion volant à 0,3 km/s (soit 1000 km/h) a une vitesse égale au millionième de celle de la lumière de sorte que l'erreur commise en utilisant l'approximation galiléenne est inférieure à un millionième de millionième (soit 10-12), tout à fait négligeable dans la pratique courante. Cependant pour des mesures très précises de temps de trajets utilisées dans les expériences spatiales et aussi par le GPS, il faut impérativement tenir compte des corrections relativistes (à la fois celles de la relativité restreinte et de la relativité générale d'ailleurs).
Pour un corps se déplaçant à une vitesse égale au dixième de celle de la lumière, l'effet relativiste est de l'ordre de un pour cent. Ainsi les effets relativistes ne deviennent significatifs que pour des vitesses proches de la célérité de la lumière, impossibles à atteindre dans la vie courante (mais pas en laboratoire : les accélérateurs de particules permettent au contraire d'atteindre des vitesses allant jusqu'à quelques mètres par seconde de moins que c seulement[16]). C'est une des raisons pour lesquelles nous avons des difficultés à appréhender concrètement le fonctionnement de la relativité restreinte.
L'intervalle d'espace-temps entre deux événements
Article détaillé : Intervalle d'espace-temps.La théorie relativiste peut donner l'impression (ne serait-ce que par son nom) de rendre les choses totalement dépendantes du référentiel (inertiel) depuis lequel sont faites les mesures. Les précédents paragraphes sur la relativité des longueurs et des durées semblent illustrer cette opinion. Pourtant ce point de vue est erroné car plus profondément la relativité restreinte s'attache au contraire à dégager ce qui est invariant par changement de coordonnées. Dans cette optique l’invariance de l'intervalle d'espace-temps entre deux événements est un élément fondateur de la théorie relativiste[17].
Dans un référentiel, un événement est caractérisé par ses coordonnées spatio-temporelles : « tel endroit, tel instant ». Deux événements situés respectivement en x1,y1,z1,t1 et en x2 y2, z2, t2 sont séparés par un intervalle d'espace-temps dont le carré est
Nous écrirons plus simplement
Cet intervalle est un invariant relativiste : sa valeur ne dépend pas du référentiel galiléen dans lequel on l'évalue. On peut le vérifier sur les formules de Lorentz).
Par suite de la présence du signe « - » le "carré" de l'intervalle d'espace-temps peut se révéler positif ou négatif : l'appellation de "carré" n'est que conventionnelle. C'est ce qui fait toute la différence avec le carré de la distance euclidienne, qui, elle, est toujours positive. On notera toutefois que les quantités Δt2 et Δs2 restent évidemment de « véritables » carrés, et à ce titre positifs.
Le signe de l'invariant d'espace-temps Δσ2 permet de classer deux événements l'un par rapport à l'autre, imagé par le cône de lumière, ce classement a un caractère absolu et correspond à leur possibilité ou non d'être liés par un lien causal.
Article détaillé : Cône de lumière.Le temps et l'espace jouent des rôles symétriques dans l'intervalle d'espace-temps, et qu'il est donc logique de les mesurer de la même façon. C'est le point de vue adopté par la nouvelle définition de la vitesse de la lumière, qui, en étant fixée de manière arbitraire, établit une équivalence de fait entre longueur et temps, en redéfinissant le mètre à partir de la seconde. Concrètement on peut mesurer une distance ou un temps indifféremment en centimètres ou en secondes.
Diagramme d'espace-temps
Article détaillé : Diagramme de Minkowski.En mécanique newtonienne, l'espace est séparé du temps et on étudie le mouvement d'une particule en fonction d'un temps absolu. Graphiquement on représente la trajectoire dans l'espace (mais pas dans le temps !). Par exemple, on trace l'ellipse que décrit une planète autour du Soleil selon les lois de Kepler. La figure ci-contre montre le trajet spatial effectué par un certain nombre de particules A, B, C, D, E, etc. animées d'une vitesse constante pendant le même laps de temps, disons une seconde, trajet proportionnel à la vitesse du mobile. Dans le cas général on peut tracer la trajectoire d'un point M (x, y, z) dans un repère cartésien à trois dimensions.
En relativité restreinte on suit des événements dans un espace à 4 dimensions, trois d'espace et une de temps, et par conséquent il est impossible dans le cas le plus général de visualiser la courbe représentant la succession d'événements traduisant le déplacement de la particule à la fois dans le temps et dans l'espace. Cette courbe est appelée ligne d'univers de la particule. Pour lever la difficulté de la représentation de 4 dimensions on se limite souvent à 2 dimensions, une d'espace et une de temps. Autrement dit on considère des mouvements seulement le long de l'axe des x, les coordonnées y et z restant inchangées. Ne restent alors que les variables x et t, lesquelles permettent de tracer dans un repère cartésien à deux dimensions la trajectoire d'une particule dans l'espace-temps : sa ligne d'univers.
Les deux figures ci-contre illustrent le passage du point de vue newtonien au point de vue relativiste. En haut on a porté l'espace parcouru en 1 seconde par diverses particules de vitesse constante. Tandis que A reste au même point, B se déplace d'une certaine quantité, C va plus vite et va plus loin, D encore plus tandis que E se déplace dans l'autre sens. Dans la figure du bas, on a porté dans un diagramme spatio-temporel la succession des événements constituant le mouvement de la particule. Puisque la vitesse des particules est constante, leur abscisse est évidemment x = v t de sorte que leur ligne d'univers est une droite. La pente de celle-ci est proportionnelle à la vitesse v.
La chose remarquable est que la ligne d'univers de la particule au repos n'est plus un seul point mais le segment de droite OA. En effet, si la particule ne bouge pas (x = constante) le temps continue à s'écouler pendant la période considérée !
Si un segment de droite représente dans ce diagramme un mouvement à vitesse constante, dans le cas général c'est une courbe quelconque qui traduira le mouvement d'une particule. À titre d'exemple considérons la ligne d'univers ci-contre représentant un mobile partant de l'abscisse x = 0 et y revenant un temps T plus tard, temps mesuré disons sur Terre. Il pourra s'agir d'une fusée effectuant un voyage aller-retour intersidéral et nous continuerons à raisonner sur cet exemple.
Le segment de droite entre « départ » et « arrivée » le long de l'axe temporel représente la ligne d'univers de la Terre, dont la coordonnée spatiale, égale à 0, ne varie pas. La ligne courbe représente la suite d'événements constituant le voyage de la fusée. La coordonnée curviligne permettant de repérer un point sur cette courbe est le temps propre de la fusée, celui que mesure l'horloge embarquée.
Les formules relativistes montrent que le temps propre le long du trajet curviligne est plus court que le temps propre le long du trajet rectiligne (ici celui qui représente le temps terrestre). Ce phénomène est le fondement du paradoxe des jumeaux. L'un des frères fait un aller-retour à une vitesse proche de la lumière (ce qui est d'ailleurs impossible à réaliser, mais il s'agit d'une expérience imaginaire) tandis que son frère reste à Terre. Au retour le voyageur se retrouve plus jeune que son frère.
Ainsi, tandis qu'en géométrie euclidienne (x, y) le chemin le plus court entre deux points A et B est la ligne droite, en géométrie lorentzienne (x, t) l'intervalle temporel entre deux événements A et B est maximum pour la particule se déplaçant le long du trajet rectiligne AB. Le voyage le plus long est celui qui correspond au trajet rectiligne AB dans le diagramme espace-temps. Dans le cas présent cette trajectoire est celle que suit un mobile libre de toute force et avançant donc à vitesse constante. Cette propriété est tellement capitale qu'elle permet de retrouver les équations de la relativité générale[18] en étendant le principe de maximisation du temps de parcours au mouvement libre d'une particule dans un champ de gravitation (au voisinage d'un trou noir ou du Soleil par exemple)[19].
Vitesse et quadri-vitesse
Loi de composition des vitesses
Dans une fusée se déplaçant à la vitesse
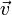 par rapport à la Terre on tire un boulet de canon à la vitesse
par rapport à la Terre on tire un boulet de canon à la vitesse 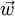 mesurée dans la fusée. Quelle est la vitesse
mesurée dans la fusée. Quelle est la vitesse 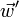 du boulet mesurée sur Terre ?
du boulet mesurée sur Terre ?En cinématique galiléenne les vitesses s'ajoutent et on aurait
En cinématique relativiste la loi de composition des vitesses est différente :
- En supposant que
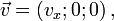 on écrit
on écrit 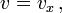 et
et 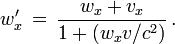
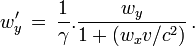
Éléments de démonstrationDans la fusée la distance Δx ’ parcourue par le boulet pendant le temps Δt’ est
En utilisant les formules de Lorentz
et en remplaçant Δx ’ par sa valeur on trouve facilement la vitesse du boulet dans le repère terrestre sous la forme :
D'où les formules.
Cette relation montre que la loi de composition des vitesses en relativité restreinte n'est plus une loi additive et que la vitesse c est une vitesse limite quel que soit le référentiel considéré (quand on lui ajoute une vitesse, on retombe sur c).
Cependant, dans le cas où les deux vitesses
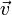 et
et 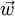 sont parallèles, il existe un paramétrage permettant d'obtenir une loi additive. Il suffit pour cela de passer de la vitesse v au paramètre angulaire de vitesse θ introduit précédemment, et appelé rapidité.
sont parallèles, il existe un paramétrage permettant d'obtenir une loi additive. Il suffit pour cela de passer de la vitesse v au paramètre angulaire de vitesse θ introduit précédemment, et appelé rapidité.Montrons que dans une composition de vitesses les paramètres angulaires de vitesse s'ajoutent.
En posant
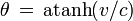 ,
,  ,
, 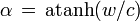 et en utilisant la formule d'addition des fonctions hyperboliques
et en utilisant la formule d'addition des fonctions hyperboliques 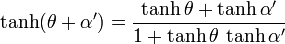 , on trouve
, on trouve 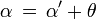
Le paramètre angulaire correspondant à la vitesse c est infini puisque artanh(x ), l'argument tangente hyperbolique de x, tend vers l'infini lorsque x tend vers 1. On retrouve donc le fait que c est une vitesse limite indépendante du repère choisi. Cette vitesse limite est impossible à atteindre pour une particule massive, seules les particules de masse nulle, comme le photon, peuvent se déplacer à la vitesse de la lumière.
- Application numérique
Imaginons qu'un obus soit tiré avec la vitesse w' = 0,75c dans le repère d'une fusée se déplaçant elle-même à la vitesse v = 0,75c par rapport à la Terre. Quelle est la vitesse du boulet mesurée sur Terre ? Clairement la valeur 1,5c que nous donnerait la formule galiléenne est fausse puisque la vitesse obtenue dépasserait celle de la lumière. Les formules relativistes nous invitent à procéder comme suit. L'angle paramétrique de vitesse de l'obus par rapport à la fusée est
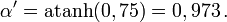 L'angle paramétrique de la vitesse de la fusée par rapport à la Terre a la même valeur
L'angle paramétrique de la vitesse de la fusée par rapport à la Terre a la même valeur 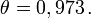 La rapidité de l'obus par rapport à la Terre est donc
La rapidité de l'obus par rapport à la Terre est donc 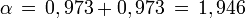 , ce qui correspond à la vitesse
, ce qui correspond à la vitesse 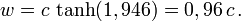
On peut évidemment retrouver ce résultat directement sur la formule donnant w en fonction de w ’ et v.
Le quadrivecteur vitesse
Article détaillé : Quadrivecteur.En mécanique newtonienne on étudie le mouvement d'un mobile en suivant sa position
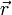 en fonction du temps t, ce temps étant supposé de caractère absolu, indépendant de l'horloge qui le mesure. En relativité on abandonne cette vision des choses pour considérer le mouvement d'une particule comme une succession d'événements
en fonction du temps t, ce temps étant supposé de caractère absolu, indépendant de l'horloge qui le mesure. En relativité on abandonne cette vision des choses pour considérer le mouvement d'une particule comme une succession d'événements 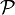 , la courbe décrite par cet événement dans un espace à quatre dimensions (trois pour l'espace, une pour le temps) prenant alors le nom de « ligne d'univers ».
, la courbe décrite par cet événement dans un espace à quatre dimensions (trois pour l'espace, une pour le temps) prenant alors le nom de « ligne d'univers ».De même qu'en mécanique classique on définit la vitesse d'une particule en prenant la dérivée
de la position par rapport au temps, de même en mécanique relativiste on définit le vecteur vitesse à quatre dimensions (ou quadrivecteur vitesse)
où
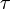 est le temps propre de la particule, défini plus haut.
est le temps propre de la particule, défini plus haut.En explicitant les composantes de ce quadrivecteur dans un repère donné on peut écrire
expression dans laquelle nous avons introduit le facteur c pour travailler avec des coordonnées homogènes.
Il existe une relation simple, et importante, relative à ce quadrivecteur. La définition du carré de l'intervalle d'espace-temps défini ci-dessus peut se généraliser à tout quadrivecteur. On définira ainsi le carré de la norme d'un quadrivecteur comme la différence entre le carré de sa partie temporelle et celui de sa partie spatiale. Et le résultat capital est que cette norme est invariante par transformation de Lorentz. Autrement dit elle ne dépend pas du repère choisi. Dans le cas de la vitesse ce résultat prend une forme particulièrement simple. En effet, dans le repère propre de la particule, la partie spatiale du quadrivecteur vitesse est nulle tandis que la partie temporelle vaut tout simplement c (dt/dτ = 1 puisque le temps t est précisément le temps τ tel qu'il est mesuré dans le repère du mobile). Autrement dit dans le repère propre d'une particule, le quadrivecteur vitesse a pour composantes (c, 0, 0, 0). Par conséquent dans tout repère galiléen on aura la relation
- (partie temporelle de
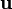 )2 - (partie spatiale de
)2 - (partie spatiale de 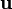 )2 = c2 .
)2 = c2 .
C'est l'invariance de cette norme qui permet de parler du quadrivecteur d'une particule indépendamment de tout système de coordonnées.
Le quadrivecteur énergie-impulsion
On peut poursuivre le raisonnement. De même que l'impulsion classique d'une particule était le produit «
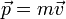 » de la masse par la vitesse, de même le produit « m
» de la masse par la vitesse, de même le produit « m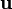 » du quadrivecteur vitesse «
» du quadrivecteur vitesse « 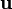 » par la masse « m » de la particule devient un quadrivecteur impulsion. On l'appelle souvent vecteur « énergie-impulsion », en exprimant ainsi le fait que énergie et impulsion sont réunies en un concept physique de manière indissociable, de la même façon que l'espace et le temps composent l'espace-temps. En effet si les composantes spatiales de ce quadrivecteur s'identifient de façon évidente à celles d'une impulsion classique, les physiciens ont été conduits par Einstein à identifier la composante temporelle de ce quadrivecteur avec l’énergie de la particule considérée. Bien que les raisons de ce choix soient multiples, il n'est pas si facile d'en donner une véritable démonstration, mais cette situation est tout à fait courante en physique[20], les hypothèses naissant en même temps que la théorie se développe et que les confirmations expérimentales se succèdent. En vérité les dizaines de milliers de confirmations expérimentales quotidiennes de la théorie ainsi imaginée, sont un gage suffisant de la justesse des hypothèses qui en constituent le fondement.
» par la masse « m » de la particule devient un quadrivecteur impulsion. On l'appelle souvent vecteur « énergie-impulsion », en exprimant ainsi le fait que énergie et impulsion sont réunies en un concept physique de manière indissociable, de la même façon que l'espace et le temps composent l'espace-temps. En effet si les composantes spatiales de ce quadrivecteur s'identifient de façon évidente à celles d'une impulsion classique, les physiciens ont été conduits par Einstein à identifier la composante temporelle de ce quadrivecteur avec l’énergie de la particule considérée. Bien que les raisons de ce choix soient multiples, il n'est pas si facile d'en donner une véritable démonstration, mais cette situation est tout à fait courante en physique[20], les hypothèses naissant en même temps que la théorie se développe et que les confirmations expérimentales se succèdent. En vérité les dizaines de milliers de confirmations expérimentales quotidiennes de la théorie ainsi imaginée, sont un gage suffisant de la justesse des hypothèses qui en constituent le fondement.Dans un repère d'inertie (par exemple le repère terrestre en première approximation, nommé ci-après repère du laboratoire) les coordonnées des évènements liés à la particule suivie sont (t, x, y, z) et les composantes dans ce repère du quadrivecteur énergie-impulsion du mobile sont :
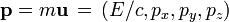 ; avec :
; avec : 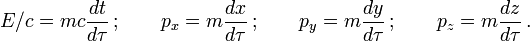
Expression relativiste de l'énergie
En tenant compte de la relation donnant le rapport entre le temps propre (le temps t’ de la fusée, ou τ de la particule en mouvement) et le temps t dans le repère considéré (repère du laboratoire), on a :
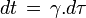
On aboutit donc à l'expression de l'énergie totale de la particule dans le repère du laboratoire, celui par rapport auquel la particule est animée de la vitesse
 (car l'énergie dépend du référentiel dans lequel on la calcule !) sous la forme de :
(car l'énergie dépend du référentiel dans lequel on la calcule !) sous la forme de :- En relativité restreinte, l'énergie totale d'une particule reste égale à la somme de l'énergie au repos m.c2 contenue dans sa masse et de l'énergie cinétique K. En tenant compte de l'expression relativiste de l'énergie, on voit que l'énergie cinétique d'une particule est donnée par l'expression :
-
- Aux "faibles" vitesses (c'est-à-dire petites devant celle de la lumière, soit tous les cas courants "classiques"), on obtient, (en première approximation) :
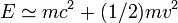
- Cette formule montre que l'énergie totale de la particule est la somme d'une énergie au repos m.c2 inconnue de la mécanique newtonienne et de l'énergie cinétique classique (1/2)m.v2 ; aux "faibles" vitesses.
-
- Pour les vitesses très proches de celle de la lumière, c'est la quantité 1 - β = [1 - (v/c)] qui compte.
- On a :
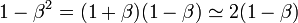
- De sorte que l'énergie totale peut alors s'écrire, (en première approximation) :
![E \simeq pc = \frac{mc^2}{\sqrt{2(1-\beta)}}\equiv \frac{mc^2}{\sqrt{2[1-(v/c)]}}](/pictures/frwiki/54/6a958361fb5fa1bbdbc1ce7dbff8c388.png)
Expression relativiste de l'impulsion
D'autre part comme les composantes de la vitesse de la particule dans le repère du laboratoire sont :
En tenant compte du facteur de dilatation du temps entre dt et dτ, on arrive à l'autre formule importante fournissant la valeur de l'impulsion dans le repère du laboratoire :
Équivalence de l'énergie et de la masse au repos
Le quadrivecteur énergie-impulsion présente la caractéristique d'avoir sa norme, ou son carré scalaire (au sens du carré d'intervalle d'espace-temps), invariante lors d'un changement de référentiel. En bref la quantité
est indépendante du référentiel dans lequel elle est calculée. Or dans le repère de la particule la vitesse est nulle, de même que l'impulsion, de sorte que la norme de cette quantité invariante vaut (m c)2. Dans n'importe quel repère on a donc la relation capitale suivante
ou encore
(Les facteurs c qui s'introduisent dans ces formules assurent leur homogénéité, p a la grandeur de m v, E celle de m v 2.)
On peut démontrer directement cette formule à partir de celles écrites ci-dessus donnant l'énergie et l'impulsion.
On peut faire plusieurs observations :
- (i) La valeur de l'énergie totale de la particule dépend du référentiel de l'observateur. Cependant, la valeur de l'énergie de masse est identique dans tous les référentiels, et en particulier dans le référentiel propre de la particule. C'est donc une caractéristique intrinsèque de la particule.
- (ii) Lorsque v tend vers c, γ tend vers l'infini, ce qui signifie qu'il faut une énergie infinie pour accélérer une particule jusqu'à atteindre la vitesse de la lumière. Cela est évidemment impossible. On arrive cependant à accélérer des particules à des vitesses très proches de c.
- (iii) La relativité restreinte apparaît dans tous les phénomènes physiques, même là où les vitesses intervenant ne sont pas relativistes. Un exemple flagrant est le défaut de masse de l'atome le plus simple : la masse de l'atome d'hydrogène
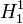 est inférieure à la somme des masses de l'électron et du proton d'une quantité juste égale à l'équivalent en masse de l'énergie d'ionisation de l'atome.
est inférieure à la somme des masses de l'électron et du proton d'une quantité juste égale à l'équivalent en masse de l'énergie d'ionisation de l'atome.
L’équivalence de la masse et de l'énergie est donnée par la célèbre E=mc². Poser cette équivalence fut un pas révolutionnaire, car les concepts de matière et d'énergie étaient distincts jusque-là, bien que certains scientifiques, comme Poincaré et Lorentz, eussent indépendamment tenté le rapprochement dans le domaine de l'électromagnétisme. De nos jours, il ne faut pas non plus surestimer cette équivalence, car tandis que la masse est la norme du quadrivecteur énergie-impulsion, l'énergie n'est que l'une des composantes de ce quadrivecteur. La masse donnée par
est invariante par changement de repère (elle est la même dans tout repère). L'énergie au contraire dépend du repère choisi, c'est évident puisque la vitesse changeant, l'énergie cinétique change aussi.
Conservation du quadrivecteur énergie-impulsion d'un système isolé
En physique classique, la quantité de mouvement et l'énergie cinétique globales d'un système isolé se conservent au cours du temps, du moins quand le chocs sont élastiques. C'est une propriété compatible mais indépendante du principe de relativité galiléen. Un changement de référentiel galiléen donne de nouvelles valeurs à l'énergie cinétique et aux cordonnées de la quantité de mouvement du système, mais ces valeurs aussi sont conservées dans le temps, dans ce référentiel.
En relativité restreinte, c'est le quadrivecteur énergie-impulsion global d'un système isolé qui se conserve, et c'est aussi une propriété compatible et indépendante du principe de relativité d'Einstein. Les coordonnées de ce vecteur à quatre dimensions (quadrivecteur) regroupe l'énergie et la quantité de mouvement, et se conservent quelleque soient les interactions entre les éléments du système isolé. De même qu'en physique non-relativiste, un changement de référentiel donne de nouvelles valeurs à l'énergie (coordonnée temporelle) et aux coordonnées de l'impulsion (coordonnées spatiales), et dans ce nouveau référentiel la conservation des valeurs de ces coordonnées, au cours du temps, est toujours valable.
Le principe de constance est le suivant :
- Indépendamment des détails de l'expérience, le quadrivecteur d'un système isolé de particules se conserve dans toute interaction interne.
Autrement dit on peut écrire :
Puisque le quadrivecteur est conservé, chacune de ses composantes dans un système de référence donné (dont les valeurs dépendent du système choisi) est également conservée dans les collisions. La composante temporelle représentant l'énergie E du système et la composante spatiale représentant son impulsion
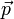 , on aboutit donc pour chaque référentiel à deux lois de conservation, l'une pour l'énergie, l'autre pour la quantité de mouvement (ou impulsion).
, on aboutit donc pour chaque référentiel à deux lois de conservation, l'une pour l'énergie, l'autre pour la quantité de mouvement (ou impulsion).- Un exemple (académique)
Une collision de deux particules est représenté dans la figure ci-contre. Une particule A de masse 8 (en unités arbitraires) animée d'une vitesse v/c de 15/17 dirigée vers la droite frappe une particule de masse 12 arrivant en sens inverse avec une vitesse v/c de 5/13 (les chiffres ont été choisis[21] pour que les calculs "tombent juste"). Après la collision, A rebondit dans l'autre sens en ayant communiqué à B une partie de sa quantité de mouvement. L'énergie totale, somme des énergies des particules A et B est conservée, de même que la quantité de mouvement totale. Les grandeurs E et p indiquées représentent en réalité (E/c2) et (p/c) et sont exprimées en unités de masse, arbitraires. Avec ces grandeurs on a la relation E 2 = p 2 + m 2. Le facteur γ est toujours défini par γ = [1 - (v/c)2]-1/2.
Collision élastique
Dans un accélérateur de particules il arrive qu'une particule de très haute énergie heurte une particule au repos et communique à cette dernière une partie de son énergie cinétique. Si les seuls échanges d'énergie concernent précisément cette énergie cinétique (conservation de la quantité de mouvement du système), on dit que le choc est élastique. Les formules traduisant la conservation du quadrivecteur du système formé par ces deux particules permet d'analyser la collision. En mécanique newtonienne la direction des deux particules après un choc forme un angle droit. Ce qui n'est pas le cas dans le cas des chocs entre particules relativistes où leurs directions forment un angle aigu. Ce phénomène est parfaitement visible sur les enregistrements de collisions effectués dans des chambres à bulles.
Considérons un électron de masse m et d'énergie très élevée frappant un autre électron intialement au repos. Les vecteurs impulsions des deux particules sont tracés sur la figure ci-contre. Avant le choc l'impulsion de l'électron incident est
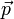 . Après le choc, les impulsions des deux électrons sont
. Après le choc, les impulsions des deux électrons sont 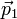 et
et 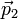 . En écrivant l'énergie d'un électron comme la somme de son énergie au repos mc2 et de son énergie cinétique K, on peut écrire l'énergie totale du système avant la collision comme :
. En écrivant l'énergie d'un électron comme la somme de son énergie au repos mc2 et de son énergie cinétique K, on peut écrire l'énergie totale du système avant la collision comme :De même,
La loi de conservation de l'énergie dit que E = E1 + E2 et par conséquent
formule indiquant bien que l'énergie cinétique est conservée elle aussi (collision élastique).
La loi de conservation de la quantité de mouvement dit que
et par conséquent si nous appelons θ l'angle entre les deux vecteurs
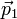 et
et 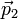 , on a la relation
, on a la relationd'où l'on tire
En exprimant le carré de l'impulsion des différents électrons en fonction de leur énergie et de leur masse à l'aide des formules indiquées ci-dessus on obtient
pour l'électron incident et
pour les électrons après le choc.
Comme K = K1 + K2 on aboutit facilement à la formule finalement simple
Cette formule montre que cos θ est positif et donc que les directions des électrons de l'état final font entre elles un angle aigu.
On trouve facilement dans la littérature[22] le traitement du cas où le choc est symétrique, les deux électrons possédant chacun la même énergie K1 = K2 = K/2. Dans cette situation particulière la formule générale devient
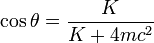 pour une collision symétrique.
pour une collision symétrique.
- Dans la limite newtonienne des faibles vitesses, les énergies cinétiques sont beaucoup plus petites que l'énergie au repos mc2 et par conséquent
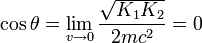
- tend vers zéro, ce qui signifie que l'angle θ tend vers π /2. C'est le résultat non relativiste.
- Dans la limite au contraire des très hautes énergies, ce sont les termes d'énergie cinétique qui sont beaucoup plus grands que le terme mc2 et par conséquent
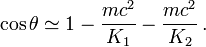
- Dans ce cas le cosinus tend vers 1, ce qui signifie que l'angle entre les vitesses des électrons tend vers zéro. Cela implique un comportement complètement différent du cas newtonien.
Les formules s'appliquent évidemment au cas de la collision entre deux protons.
Diffusion Compton
Une application physique des formules de conservation de l'énergie et de la quantité de mouvement d'un système de particules est fournie par l'analyse de la collision entre un photon de haute énergie et un électron au repos, choc constituant ce que l'on appelle la diffusion Compton.
Article détaillé : Diffusion Compton.Référentiel du centre d'inertie et masse d'un système de particules
Supposons connu un système isolé et constitué de particules sans interaction, dans un référentiel R :
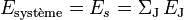 et
et 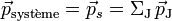 sont connus et restent inchangés au cours du temps, dans ce référentiel.
sont connus et restent inchangés au cours du temps, dans ce référentiel.En physique classique, les définitions du centre d'inertie, et d'un référentiel inertiel où ce centre est immobile, ne posent pas de problème : on utilise les vecteurs distances et les masses des corps. En physique relativiste, une définition semblable se heurte à une difficulté de choix (faut-il choisir les masses ou les énergies ?) sans critère décisif.[12]
La définition employée est celle qui permet d'utiliser les égalités relativistes le plus simplement : le référentiel dit « du centre d'inertie » est le référentiel R* dans lequel l'impulsion totale est nulle, soit
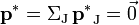 .
.Dans ce référentiel, l'énergie E* du système vérifie l'égalité
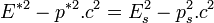 car il ne s'agit que d'un changement de référentiel, donc
car il ne s'agit que d'un changement de référentiel, donc 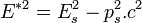 .
.La vitesse relative entre les référentiels R et R*, notée
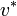 , vérifie
, vérifie 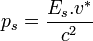 , mais cette vitesse est rarement utilisée dans les calculs.
, mais cette vitesse est rarement utilisée dans les calculs.La valeur de la masse totale M* du système ainsi obtenue est indépendante du repère dans lequel on l'évalue :
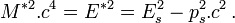 Cette invariance par rapport aux changements de référentiel, et la vérification des formules du quadrivecteur impulsion du système font que cette définition répond à toutes les propriétés attendues pour une masse.
Cette invariance par rapport aux changements de référentiel, et la vérification des formules du quadrivecteur impulsion du système font que cette définition répond à toutes les propriétés attendues pour une masse.Par la conservation de l'énergie, et l'absence d'interaction (il n'y a donc pas d'énergie dans le système qui y soit consacrée), on a :
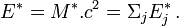
Or l'énergie Ej* de chaque particule j (dans le repère R*) est la somme de l'énergie mj c2 correspondant à sa masse au repos mj additionnée à son énergie cinétique Kj* (toujours dans le repère R*), c'est-à-dire :
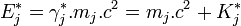 . D'où :
. D'où :Ce qui montre que : la masse totale d'un système de particules indépendantes est supérieure à la somme des masses individuelles des particules.
La non-conservation de la masse
La conservation du quadrivecteur énergie-impulsion explique que dans une réaction la masse d'un système puisse ne pas se conserver pour se transformer en énergie, en partie ou en totalité. C'est ce qui se passe dans les réactions de fission, de fusion et d'annihilation de particules.
Fission spontanée d'une particule
Supposons qu'un corps au repos, de masse M, se désintègre spontanément en deux parties de masses (masses au repos) respectives
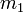 et
et 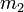 : on montre qu'alors la masse M est supérieure à
: on montre qu'alors la masse M est supérieure à 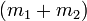 et que la différence prend la forme d'une énergie cinétique.[23]
et que la différence prend la forme d'une énergie cinétique.[23]La loi de conservation de l'énergie donne
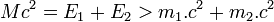 car
car 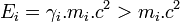 , et donc
, et donc 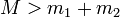 .
.Dans le cas où
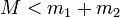 , cette désintégration ne peut pas être spontanée, elle ne peut se réaliser qu'après apport d'une énergie au moins égale à son « énergie de liaison » égale à
, cette désintégration ne peut pas être spontanée, elle ne peut se réaliser qu'après apport d'une énergie au moins égale à son « énergie de liaison » égale à 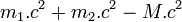 .
.La loi de conservation de l'impulsion donne
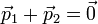 , donc
, donc 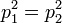 , d'où on tire
, d'où on tire 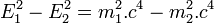 .
.Finalement, les égalités
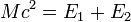 et
et 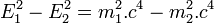 permettent de déterminer les énergies des deux nouvelles particules :
permettent de déterminer les énergies des deux nouvelles particules : 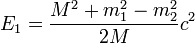 et
et 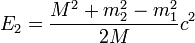 . La différence de masses
. La différence de masses 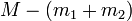 s'est convertie en énergie cinétique pour les deux nouvelles particules, énergie que l'on retrouve dans
s'est convertie en énergie cinétique pour les deux nouvelles particules, énergie que l'on retrouve dans 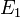 et
et 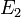 .
.On peut également calculer la norme des impulsions des deux particules, et donc aussi de leurs vitesses.
Une fission de particule implique aussi la conservation de nombres quantiques : la charge électrique, le spin, etc.
Cas des particules de masse nulle
Les expressions donnant E et p en fonction de m et v conduisent immédiatement à la formule
Si la vitesse de la particule est égale à la vitesse de la lumière, alors p = E / c en calculant E2 − p2c2 on voit que la masse de la particule est forcément nulle. En sens inverse, si la masse de la particule est nulle, alors p = E / c et par conséquent v = c.
Nous aboutissons donc à la conclusion double importante selon laquelle les particules matérielles ne peuvent pas atteindre la vitesse de la lumière et que seules des particules sans masse se déplacent à la vitesse de la lumière.
L'ensemble est parfaitement cohérent : tout mécanisme de propagation d'énergie à la vitesse de la lumière correspond à une quantité de mouvement p égale à l'énergie et donc à une « masse au repos » nulle. En sens inverse, une particule de masse nulle se déplace forcément à la vitesse de la lumière.
Exemples des rayons cosmiques et des muons
On détecte en astronomie des particules porteuses d'une énergie colossale : les rayons cosmiques. Bien que leur mécanisme de production demeure encore mystérieux, on peut mesurer leur énergie. Les nombres considérables que l'on obtient montrent que leur analyse exige l'emploi des formules de la relativité restreinte. Les rayons cosmiques fournissent donc une illustration idéale de la théorie d'Einstein.
On détecte des particules jusqu'à des énergies invraisemblables de l'ordre de 1020 électron-volts, soit cent millions de TeV. Supposons donc qu'un rayon cosmique soit un proton de 1020 eV. Quelle est la vitesse de cette particule ?
Dans l'expression donnant l'énergie E, le terme m c2 représente l'énergie de la masse au repos de la particule. Celle du proton est d'environ 1 GeV, soit 109 eV. Le rapport entre E et m c2 est donc égal à 1020/109=1011 et n'est autre que le fameux facteur d'étirement du temps γ = [1 − (v / c)2] − 1 / 2. Quelle est la vitesse de ce proton ? En écrivant
![1 - (v/c)^2=[1+(v/c)][1 - (v/c)]\simeq 2 [1 - (v/c)]](/pictures/frwiki/97/a331b82326d6bb1c51e740c61eee2d67.png) on trouve que
on trouve queAutrement dit la vitesse du proton considéré est quasiment égale à la vitesse de la lumière. Elle n'en diffère que par moins de 10-22 (mais ne peut en aucun cas l'égaler).
Voyons ce que ces chiffres impliquent pour les facteurs relativistes existant entre le repère propre de la particule et le repère terrestre. Notre propre Galaxie,de diamètre environ cent milleannées-lumière est traversée par la lumière en cent mille ans. Par conséquent pour un observateur terrestre le proton traverse cette Galaxie dans le même temps. L'extraordinaire c'est que dans le repère du proton relativiste, le temps correspondant est 1011 fois plus faible, et vaut donc 30 secondes (une année fait 3×107 secondes) !
- Notre proton ultra-relativiste et ultra-énergétique traverse notre Galaxie en 30 secondes de son temps propre mais en 100 000 ans de notre temps terrestre.
Lorsque ce rayon cosmique heurte un atome d'oxygène ou d'azote de l'atmosphère terrestre à une altitude de l'ordre de 20 à 50 kilomètres au-dessus du sol, une gerbe de particules élémentaires se déclenche contenant en particulier des muons. Une partie d'entre eux se dirigent vers le sol avec une vitesse pratiquement égale à celle de la lumière, de 300 000 kilomètres par seconde dans le repère terrestre. Ces particules traversent donc les quelque 30 kilomètres d'atmosphère en 10-4 seconde (ou 100 microsecondes).
Dans le repère où il est au repos, un muon a une demi-vie de 2 μs (2 microsecondes, ou 2×10-6 s). Cela signifie que parmi un ensemble de muons produits au sommet de l'atmosphère, la moitié auront disparu au bout de 2 microsecondes, transformés en d'autres particules. Une moitié des muons restants disparaîtront au bout d'encore 2 microsecondes et ainsi de suite. Si la demi-vie était la même (2 microsecondes) dans le repère terrestre, en 10-4 seconde de traversée de l'atmosphère les muons auraient compté 10-4 / 2×10-6 = 50 demi-vies. Par conséquent leur nombre serait réduit à l'arrivée au sol par un facteur de (1/2)50soit environ 10-15 de sorte qu'en pratique aucun muon ne l'atteindrait.
Or les mesures indiquent qu'environ 1/8, soit (1/2)3, des muons initiaux parviennent à la surface terrestre, ce qui prouve qu'ils n'ont subi que 3 divisions de leur nombre par 2 et non 15. Autrement dit le temps de traversée de l'atmosphère dans leur repère propre est de 3 demi-vies et non 50, soit 6 microsecondes seulement (et non 100 microsecondes). Ce résultat constitue une preuve forte de la justesse de la relativité restreinte et notamment du phénomène d'étirement du temps propre (ici celui du muon) lorsqu'on effectue les mesures dans un repère extérieur (ici celui de la Terre). Dans l'exemple numérique choisi le facteur de dilatation du temps γ = [1 − (v / c)2] − (1 / 2) est de 100/6.
On peut en déduire la vitesse et l'énergie des muons. En effet, on a comme dans le calcul précédent
ce qui conduit à
Comme la masse d'un muon est d'environ 100 MeV, l'énergie de la particule est 100/6 fois plus grande, soit d'environ 2000 MeV ou 2 GeV.
Électromagnétisme et relativité restreinte
Dans l'espace newtonien à trois dimensions, une particule de charge q placée dans un champ électrique
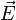 et un champ magnétique
et un champ magnétique 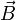 est soumise à la force de Lorentz et l'équation qui régit son mouvement est
est soumise à la force de Lorentz et l'équation qui régit son mouvement estPour transposer cette formule en mécanique relativiste, on devra considérer le quadrivecteur énergie-impulsion
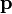 à la place du vecteur
à la place du vecteur 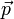 et évaluer le taux de variation de ce quadrivecteur non dans le repère d'un observateur galiléen quelconque mais dans le repère propre de la particule. Le membre de gauche sera donc de la forme
et évaluer le taux de variation de ce quadrivecteur non dans le repère d'un observateur galiléen quelconque mais dans le repère propre de la particule. Le membre de gauche sera donc de la forme 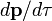 , où τ est le temps propre de la particule chargée. À droite on trouvera un objet indépendant du repère choisi et qui en outre sera forcément une fonction linéaire de la vitesse
, où τ est le temps propre de la particule chargée. À droite on trouvera un objet indépendant du repère choisi et qui en outre sera forcément une fonction linéaire de la vitesse  de la particule. En effet la partie spatiale de l'équation de la dynamique est linéaire en
de la particule. En effet la partie spatiale de l'équation de la dynamique est linéaire en 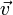 puisqu'elle s'écrit
puisqu'elle s'écritDans cette expression
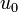 et
et  sont les composantes dans un repère lorentzien du quadrivecteur vitesse
sont les composantes dans un repère lorentzien du quadrivecteur vitesse 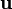 , lequel peut donc s'écrire :
, lequel peut donc s'écrire :De façon explicite l'équation ci-dessus se décompose sur les trois axes de la façon suivante :
De son côté la composante temporelle de l'équation de la dynamique (qui correspond à la loi donnant la variation de l'énergie) s'écrit
où W est le travail de la force
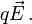
En rassemblant les équations écrites ci-dessus dans le cadre d'un espace-temps à quatre dimensions, le taux de variation du quadrivecteur énergie-impulsion est donné par
L'équation matricielle que nous venons d'écrire montre qu'en relativité restreinte le champ magnétique et le champ électrique constituent une entité unique. En réalité la présentation précédente est quelque peu incorrecte dans la mesure où pour tirer parti de toute la puissance de la théorie relativiste il est nécessaire de faire appel aux tenseurs. L'équation matricielle ci-dessus est la traduction en termes de composantes de l'équation tensorielle, indépendante, elle, de tout système de coordonnées
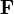 est le tenseur du champ électromagnétique (ou tenseur de Maxwell ou tenseur de Faraday). C'est cet objet qui représente physiquement le champ électromagnétique. Ses composantes dans un certain système de coordonnées sont données par la matrice écrite ci-dessus.
est le tenseur du champ électromagnétique (ou tenseur de Maxwell ou tenseur de Faraday). C'est cet objet qui représente physiquement le champ électromagnétique. Ses composantes dans un certain système de coordonnées sont données par la matrice écrite ci-dessus.Vocabulaire
- Observateur : humain ou appareil de détection possédant une horloge lui permettant de lire l'heure et éventuellement, s'il fait partie d'un groupe constitué, portant une marque indiquant sa position.
- Référentiel galiléen, appelé aussi « référentiel de Lorentz » ou « référentiel inertiel » : ensemble d'observateurs se déplaçant librement dans l'espace loin de toute masse, dont les distances mutuelles ne changent pas au cours du temps (ils sont au repos les uns par rapport aux autres) et qui ont synchronisé leurs horloges.
- Événement : un événement est un événement (!), comme par exemple la naissance d'un individu, le départ d'une fusée ou le tir d'un pétard. Il est indépendant des coordonnées de temps et d'espace qui permettent éventuellement de le localiser. Cependant il est commode en pratique de repérer les événements par leurs coordonnées relativement à un repère, à savoir le point où l'événement se produit et la date à laquelle il se produit dans ce repère.
En relativité restreinte une longueur et un temps devraient se mesurer avec la même unité (ce que nous n'avons pas fait ici de façon systématique). En astronomie on choisit l'unité de temps et on mesure une distance par le temps qu'il faut à la lumière pour couvrir cette distance. Par exemple qu'une galaxie soit située à cinq millions d'années-lumière de la nôtre signifie que la lumière met cinq millions d'années pour parcourir la distance qui nous en sépare. Remarquons que dans la vie courante on dira facilement que Paris, par exemple, est à trois heures de train de Montpellier, ce qui revient exactement à mesurer une distance en temps. D'ailleurs, depuis 1983, l'unité de temps (la seconde) est la seule a être définie directement par le système international d'unités (SI), l'unité de longueur (le mètre) étant défini comme la distance que parcourt la lumière en un temps précis (ce qui revient à fixer définitivement et exactement la valeur de c à 299 792 458 m/s)[24].
Bibliographie
Une sélection des œuvres d'Einstein, notamment ses articles originaux, sont aujourd'hui disponibles en traduction française commentée sous le titre Œuvres choisies aux éditions du Seuil/CNRS éditions, dans la collection Sources du savoir (6 volumes parus depuis 1989). Les tomes 2 et 3 sont exclusivement consacrés aux théories de la relativité.
Ouvrages de vulgarisation
- Albert Einstein, La relativité, Gauthier-Villars (1956). Réédité par Payot (1990) (ISBN 2228882542). Au format poche, un exposé élémentaire des principes de la théorie de la relativité restreinte et générale, par son auteur.
- Banesh Hoffmann, Histoire d'une grande idée : la relativité, Éditions Pour La Science (1985), diffusion Belin (ISBN 978-2-8424-5019-9). Un exposé remarquable pour sa clarté et sa simplicité de la relativité, par un ancien collaborateur d'Einstein à l'Institute for Advanced Studies de Princeton.
- Thibault Damour, Si Einstein m'était conté, Editions du Cherche-midi, Paris (2005) (ISBN 2-74910-390-8). Le grand spécialiste français des théories de la relativité nous livre enfin « son » Einstein sans équations. Thibault Damour est professeur permanent à l'Institut des Hautes Études Scientifiques (IHES) de Bures-sur-Yvette ; il a longtemps enseigné la relativité générale au DEA de physique théorique de la rue d'Ulm.
- Albert Einstein & Leopold Infeld, L'évolution des idées en physique, Collection Champs, Flammarion (1993) (ISBN 978-2-08-081119-6). Au format poche, une histoire de la physique, de la Mécanique de Newton jusqu'aux théories modernes (relativité, quanta), écrite en 1936 par Einstein lui-même et l'un de ses disciples à Princeton, pour financer le séjour de ce dernier.
- Brian Greene, L'Univers élégant, Folio essais (2005) (ISBN 2-07-030280-6). Une présentation de la tentative d'unification de la physique par la théorie des cordes.
Ouvrages d'initiation au formalisme
Accessibles au niveau premier cycle universitaire.
- James H. Smith, Introduction à la relativité, InterEditions (1968). 2e édition avec exercices corrigés (1979) ISBN 2-7296-0088-4. Réédité par Masson (Dunod - 3e édition - 1997), ISBN 2-225-82985-3. Un livre en français qui expose les bases de la théorie de façon claire.
- M. Boratav & R. Kerner, Relativité, Ellipses (1991), ISBN 2-7298-9145-5. Un très bon livre en français, écrit dans un style très vivant par deux professeurs à l'Université Paris 6. Contient de nombreux exemples et applications issus d'expériences récentes.
- E.F. Taylor & John A. Wheeler, À la découverte de l'espace-temps, Dunod (1970). Cet ouvrage original est une introduction élémentaire, quoique rigoureuse, à la théorie de la relativité restreinte ; Wheeler est un expert incontesté du domaine. Le public visé est l'étudiant de premier cycle débutant en physique ; en particulier, la connaissance de l'électromagnétisme n'est pas nécessaire. C'est le complément idéal pour prolonger la lecture du livre de Banesh Hoffman cité ci-dessus. De nombreux exercices, dont une bonne part résolue. Malheureusement plus édité en français, cet ouvrage reste disponible en anglais : Spacetime Physics, W. H. Freeman (2e édition - 1992), ISBN 0-7167-2327-1.
- Jean-Marc Levy-Leblond, Les relativités, Cahiers de Fontenay n° 8, École Normale Supérieure de Fontenay-aux-Roses (1977). Notes de cours très pédagogiques, hélas non publiées. Disponibles dans les bonnes bibliothèques universitaires, et au format pdf, avec l'aimable autorisation de Jean-Marc Lévy-Leblond et de l'Ecole normale supérieure de Fontenay-aux-Roses http://o.castera.free.fr/pdf/Les%20relativit%C3%A9s.pdf
- Max Born, La théorie de la relativité d'Einstein et ses bases physiques, Gauthier-Villars (1923). Réédité par Jacques Gabay (2003) ISBN 2-87647-230-9. Cet ouvrage, écrit par un grand théoricien allemand, prix Nobel 1954, est remarquable pour sa clarté. La place occupée par l'aspect mathématique y est extrêmement réduite.
- Albert Einstein, La théorie de la relativité restreinte et générale, Dunod (2005) ISBN 2100487167. La version anglaise se trouve sur le projet Gutenberg
- Albert Einstein, Quatre conférences sur la théorie de la relativité, Dunod (2005) ISBN 2100492292. Texte de quatre conférences prononcées à l'université de Princeton en 1921.
- Thibault Damour & Stanley Deser, Relativité, Encyclopeadia Universalis 19 (1995) 739-748. Un exposé non technique d'une grande clarté, par un spécialiste de notoriété mondiale : Thibault Damour est professeur permanent à l'Institut des Hautes Études Scientifiques (I.H.E.S.) de Bures-sur-Yvette ; il a longtemps enseigné la relativité générale au D.E.A. de physique théorique de Paris.
- Jean-Pierre Provost & Marie-Antoinette Tonnelat, Espace-temps, Encyclopeadia Universalis 8 (1995) 743-745. Un exposé d'introduction assez simple, ou l'essentiel de la relativité en quatre pages.
- Hubert Lumbroso, Relativité - Problèmes résolus, Édisciences (2e édition 1996) ISBN 2-84074-127-X. Ouvrage classique de taupe : un résumé de cours, avec un très grand nombre de problèmes corrigés.
- Wolfgang Rindler, Introduction to special relativity, Oxford University Press (2e édition-1991) ISBN 0-19-853952-5. Une introduction écrite par un professeur de l'Université de Dallas (Texas), spécialiste mondial du domaine.
- N.D. Mermin, It's about time: understanding Einstein's relativity, Princeton university press (2005), ISBN 0-691-12201-6.
- David Bohm, The special theory of relativity, Benjamin (1965), réédité par Routeledge (Londres-1996) ISBN 0-415-14808-1. Il s'agit du cours professé au Birbeck College de l'Université de Londres par David Bohm, théoricien de la physique quantique, récemment disparu. Le formalisme mathématique est réduit au strict nécessaire permettant de discuter les idées physiques sous-jacentes. Niveau premier cycle universitaire.
- Wolfgang Rindler, Relativity : special, general and cosmological, Oxford University Press (3e édition-2001) ISBN 0-19-850836-0. Une introduction brillante à tous les aspects de la relativité, par un professeur de l'Université de Dallas (Texas), spécialiste mondial du domaine. Accessible dès le premier cycle universitaire.
- Wolfgang Rindler, Essential relativity : special, general and cosmological, Texts and Monographs in Physics, Springer-Verlag (2e édition révisée-1977) ISBN 3-540-10090-3. Édition antérieure du livre précédent, toujours intéressante.
- George F.R. Ellis & Ruth M. Williams, Flat & curved space-times, Oxford University Press (2e édition-2000) ISBN 0-19-850656-2. Une autre excellente introduction à la relativité, par un expert, professeur de l'Université de Cape-Town (Afrique du Sud), et sa collaboratrice. Accessible dès le premier cycle universitaire.
- Clifford M. Will, Tests of special relativity, Séminaire Poincaré « Einstein, 1905-2005 » (9 avril 2005). Ce texte en anglais, écrit par le spécialiste mondial des aspects expérimentaux des deux théories relativistes d'Einstein, décrit quelques tests expérimentaux de la relativité restreinte. À télécharger ici aux formats PostScript ou PDF.
- Julian Schwinger, L'héritage d'Einstein - Les prolongements de la relativité, Collection L'univers des sciences, Bibliothèque Pour La Science (1988). Une présentation relativement simple de la théorie d'Einstein par un théoricien américain, prix Nobel de physique 1965 (avec Feynman et Tomonaga) pour la théorie de l'électrodynamique quantique. Vulgarisation de niveau premier cycle universitaire (il y a quelques équations simples).
- Lewis C. Epstein, Relativity Visualized.
Aspects historiques
- Olivier Darrigol, Faut-il réviser l'histoire de la relativité ?, La Lettre de l'Académie des Sciences 14 (Hiver 2004) 6-7. L'auteur est physicien théoricien de formation. Il travaille au laboratoire de recherches épistémologiques et historiques sur les sciences exactes et les institutions scientifiques (REHSEIS) du CNRS et de l'Université Paris VII.
- Albert Einstein, Œuvres choisies - Tome 2 : Relativités I, Seuil / CNRS Editions (1999), ISBN 2-02-010179-3.
- Albert Einstein, Œuvres choisies - Tome 3 : Relativités II, Seuil / CNRS Editions (1999), ISBN 2-02-010180-7.
- Marie-Antoinette Tonnelat, Histoire du principe de relativité, Nouvelle Bibliothèque Scientifique, Flammarion (1971) ASIN 2082101630. Une histoire monumentale, depuis l'Antiquité jusqu'aux théories d'Einstein. Comporte une imposante bibliographie. Même s'il contient peu d'équations, ce livre exige de l'attention de la part du lecteur. Certains passages techniques consacrés à la théorie de la relativité générale sont de niveau deuxième cycle universitaire minimum.
- Abraham Pais, Albert Einstein - Sa vie, son œuvre, Interéditions (1993). Réédité par Dunod (2005) ISBN 2-10-049389-2. La biographie scientifique qui fait aujourd'hui autorité depuis sa parution en anglais en 1982[réf. nécessaire], par un professeur de l'Université de Rockfeller qui a connu Einstein dans les dernières années de sa vie. Contenu extrêmement riche. Le niveau de certains passages techniques est celui d'un second cycle universitaire (au moins).
- Arthur I. Miller, Albert Einstein's special theory of relativity - Emergence (1905) & early interpretation (1905-1911), Addison-Wesley (1981). Réédité par Springer-Verlag (1998) ISBN 0-387-94870-8. Une étude extrêmement érudite des premiers pas de la théorie.[réf. nécessaire]
- Wolfgang Pauli, Theory of relativity, Dover Publications, Inc. (1981) ISBN 0-486-64152-X. Ce livre est une réédition anglaise d'un article de revue écrit en allemand en 1921 pour l'Encyklopädie der Mathematischen Wissenschaften par Pauli. Voilà ce qu'en dit Einstein dans une lettre adressée à Born, son professeur à Göttingen, datée du 30 décembre 1921 : « Pauli est un type épatant pour ses 21 ans ; il peut être fier de son article pour l'Encyclopédie. ».
- Françoise Balibar, Galilée, Newton lus par Einstein - Espace & Relativité, Collection Philosophies, Presses Universitaires de France (1984) ISBN 2-13-043493-2. Réflexions historiques sur le principe de relativité, en 128 pages (format poche). Il ne s'agit pas d'un exposé de la théorie d'Einstein.
Biographies d'Einstein
- Banesh Hoffmann, Albert Einstein, créateur et rebelle, Collection Points-Sciences, Le Seuil (1975) ISBN 2-02-005347-0. Une excellente biographie au format poche, par un ancien collaborateur d'Einstein à l'Institute for Advanced Studies de Princeton.
- Philippe Frank, Einstein - Sa vie et son temps, Collection Les savants & le monde, Albin Michel (Paris-1950). Réédition en poche dans la collection Champs, Flammarion (1993) ISBN 2080812424. Une biographie autorisée de première main, par celui qui fut le successeur d'Einstein à la chaire de physique théorique de l'Université de Prague, nommé sur sa recommandation. Très documentée, elle décrit admirablement le contexte historique (scientifique et politique) de la genèse des travaux d'Einstein.
- Abraham Pais, Albert Einstein - Sa vie, son œuvre, Interéditions (1993). Réédité par Dunod (2005) ISBN 2-10-049389-2. La biographie scientifique qui fait aujourd'hui autorité depuis sa parution en 1982, par un professeur de l'Université de Rockfeller qui a connu Einstein dans les dernières années de sa vie. Contenu extrêmement riche. Le niveau de certains passages techniques est celui d'un second cycle universitaire (au moins).
- Jacques Merleau-Ponty, Einstein, Collection Champs, Flammarion (1997) ISBN 2080813382. Une autre biographie au format poche, par un professeur d'épistémologie de l'Université de Paris X - Nanterre. L'ouvrage est divisé en trois parties : l'homme, son œuvre scientifique et sa philosophie.
- Françoise Balibar, Einstein : La joie de la pensée, collection Découvertes, Gallimard (1993), ISBN 2-07-053220-8.
- Kouznetsov Boris, Einstein sa vie / sa pensée / ses théories, Belgique, Marabout Université, Des presses de Gérard & co, 1967, 336 p.
Notes et références
- ↑ La nouvelle "The last time around" de Robert Berghe, traduit par "la dernière fois" dans l'anthologie "histoire d'immortels", utilise ce sujet comme thème central. Il est aussi mentionné comme un facteur de décalage temporel dans "The Dreamweaver's Dilemma" de Lois McMaster Bujold.
- ↑ (en) James Clerk Maxwell, « A Dynamical Theory of the Electromagnetic Field », dans Philosophical Transactions of the Royal Society of London, vol. 155, 1865, p. 459-512 [[pdf] texte intégral]
- ↑ On pourra en trouver la traduction en français commentée par Anatoly A. Logunov., directeur de l'Institut de physique des hautes énergies (Protvino, Russie), membre de l'Académie des sciences de Moscou. Henri Poincaré, « Sur la dynamique de l'électron », dans une note de l'Académie des sciences, 1905 [texte intégral]
- ↑ (de) Albert Einstien, « Zur Elektrodynamik bewegter Körper », dans Annalen der Physik, vol. 17, 30 juin 1905, p. 891-921 [texte intégral] [(en) lire en ligne]
- ↑ {en} http://www-gap.dcs.st-and.ac.uk/~history/HistTopics/Special_relativity.html
- ↑ Biographie d'Albert Einstein
- ↑ « ...for his services to Theoretical Physics, and especially for his discovery of the law of the photoelectric effect »
- ↑ J. Kunz ; American Journal of Science 30 (1910) 1313.
- ↑ D.F. Comstock ; Physical Review 30 (1910) 267.
- ↑ Le cas c2 fini négatif est exclu, car la théorie ne possèderait plus alors aucune notion de causalité.
- ↑ Le lecteur intéressé par cet aspect peut consulter, par exemple, Les relativités, Jean-Marc Levy-Leblond, Les relativités, Cahiers de Fontenay n° 8, École Normale Supérieure de Fontenay-aux-Roses (1977), ou encore le paragraphe 2.17, Special Relativity Without the Second Postulate, dans Essential relativity : special, general and cosmological de Wolfgang Rindler. Voir aussi Essential relativity : special, general and cosmological, Texts and Monographs in Physics, Springer-Verlag (2e édition révisée-1977) ISBN 3-540-10090-3, édition antérieure du livre précédent, toujours intéressante.
- ↑ a et b James H. Smith, Introduction à la relativité, InterEditions (1968). 2e édition avec exercices corrigés (1979) ISBN 2-7296-0088-4. Réédité par Masson (Dunod - 3e édition - 1997), ISBN 2-225-82985-3.
- ↑ Pendant ces γ secondes la fusée de vitesse v parcourt la distance γ v dans le repère terrestre, cette quantité représentant donc la distance entre l'observateur voyant en face de lui le top donné n° p et l'observateur voyant le top suivant n° (p + 1).
- ↑ On verra dans l'article détaillé paradoxe des jumeaux que le paradoxe a néanmoins été confirmé expérimentalement à l'aide d'horloges atomiques
- ↑ Tous ces paradoxes sont étudiés en détail par Taylor et Wheeler(en)E.F. Taylor, J.A. Wheeler, Spacetime Physics, W.H. Freeman and Company, 1966 ; le paradoxe de l'automobile et du garage, intitulé The pole and barn paradox, est analysé en page 70.
- ↑ Large Hadron Collider#Les faisceaux de protons
- ↑ On peut consulter à ce propos Un conte pour comprendre la relativité restreinte, qui présente la théorie relativiste sous une forme ludique en se basant sur la propriété d'invariance de l'intervalle spatio-temporel
- ↑ Idée utilisée par David Hilbert dès 1916 : voir principe de moindre action
- ↑ Taylor et Wheeler fondent une présentation simple de la relativité générale : (en)E.F. Taylor & J.A. Wheeler, Exploring Black Holes, Introduction to General Relativity, Addison Wesley Longman, 2000 . Les auteurs se basent sur le principe selon lequel un mobile libre de toute force se déplace le long du chemin rendant maximale la durée propre du trajet. Ils l'appellent en anglais le Principle of Extremal Aging
- ↑ voir La Science et l'Hypothèse de Henri Poincaré. Citons encore ce texte de Misner, Thorne et Wheeler, Gravitation, Freeman, 1970, page 71 : (en) « All the laws and theories of physics […] have this deep and subtle character, that they both define the concepts they use and make statements about these concept. […] Any forward step in human knowledge is truly creative in this sense: that theory, concept, law and method of measurement -forever inseparable- are born into the world in union. »
- ↑ (en)E.F. Taylor, J.A. Wheeler, Spacetime physics, Introduction to special relativity, second edition, Freeman, 1992, p 207
- ↑ voir par exemple (en)E.F. Taylor, J.A.Wheeler, Spacetime physics, Introduction to special relativity, second edition, Freeman, 1992, p 240
- ↑ Lev Landau et Evguéni Lifchitz, Physique théorique, tome 2 : Théorie des champs, éd. MIR, Moscou [détail des éditions], §11.
- ↑ Mètre
Voir aussi
Articles connexes
- Covariance
- Espace de Minkowski
- Formulaire de relativité restreinte
- Intervalle d'espace-temps
- Invariance de Lorentz
- Le voyage dans le futur des autres où l'effet Doppler est utilisé pour analyser le paradoxe des jumeaux dans le cadre de la relativité restreinte.
- Limitation de vitesse (physique)
- Paradoxe des jumeaux
- Paradoxe du train
- Petites expériences de pensée
- Principe de moindre action
- Quatrième dimension
- Relativité générale
- Théories d'une vitesse de lumière variable
- Vitesse de la lumière
- (histoire des sciences) Controverse sur la paternité de la relativité
Liens externes
- (fr) Un conte pour comprendre la relativité restreinte une page web accessible au niveau du premier cycle universitaire écrite par un astrophysicien et présentant les formules relativistes sous forme ludique
- (de) Relativité restreinte œuvre originale en Allemand, Annalen der Physik, Berne 1905
- (fr) Approche conceptuelle et géométrique n'utilisant pas les formules de Lorentz
- (fr) Relativité restreinte et naissance de l'espace-temps, Futura Sciences
- (fr) La relativité restreinte et l'invariance de Lorentz, Futura Sciences, 5 juillet 2007
- (fr) J.L. Bobin, cours de physique. Un cours de l'université Pierre et Marie Curie de niveau L3.
- (fr) La relativité restreinte à l'aide de diagrammes, R.Beauchamp, Collège Bois-de-Boulogne (Montréal)
- (fr) Cours d'électrodynamique relativiste des postulats aux équations de Maxwell covariantes en passant par la démonstration du champ tenseur (sommaire accessible en milieu de page avec version téléchargeable écrite en LaTeX en fin de chaque cours)
- (en) Idées Lumineuses, une animation humoristique sur la relativité restreinte pour le grand public, Yannick Mahé, 2005
- (en) Reflections on Relativity, livre en html, l'auteur est Kevin Brown [1].
- (en) One more derivation of the Lorentz transformation, Jean-Marc Lévy-Leblond.
- (fr) Les relativités, Jean-Marc Lévy-Leblond, Les Cahiers de Fontenay (n°8).
- Portail de la physique
Catégories : Physique théorique | Relativité | Albert Einstein
Wikimedia Foundation. 2010.


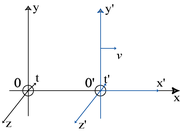
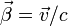
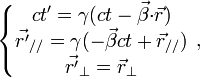
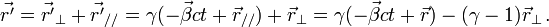
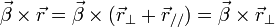
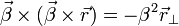
![\left\{\begin{matrix}
ct'=\gamma(ct-\vec{\beta}{\cdot}\vec{r})\\
\vec{r'}=\gamma(-\vec{\beta}ct + \vec{r})+[(\gamma-1)/\beta^{2}]\,\vec{\beta}\times(\vec{\beta}\times\vec{r})\\
\end{matrix}\right.](/pictures/frwiki/50/2722995ac8211ee563452dd9f8d60f92.png)
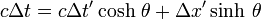
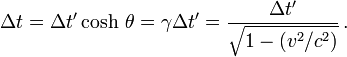
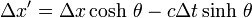
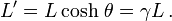
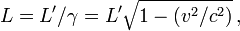
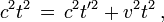
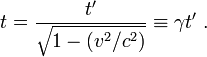
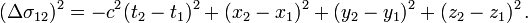
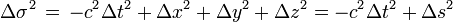

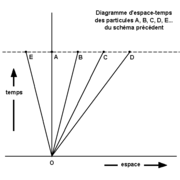

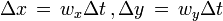
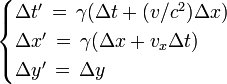
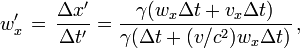
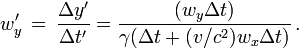
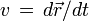
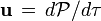
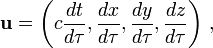
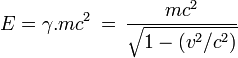
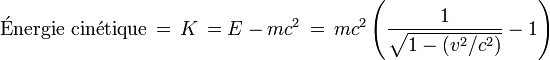
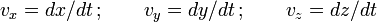
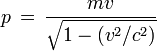

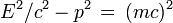
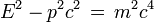
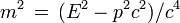
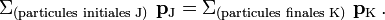

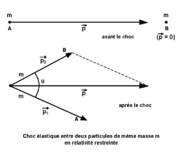
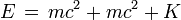
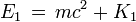
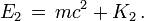
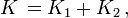
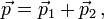
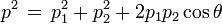
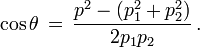
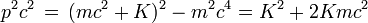
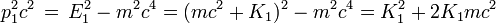
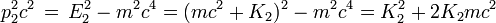
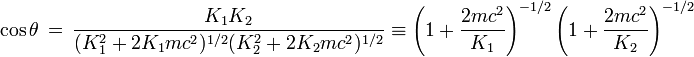
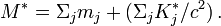
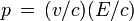
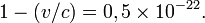

![1 - (v/c)^2\,=\,2\times[1 - (v/c)]\,=\,(6/100)^2\,,](/pictures/frwiki/51/387f2ffe52b63cf33d13e16ab416a07a.png)